Redes Neurais

Otimização Contínua

Prof. Jodavid Ferreira

UFPE

Motivação:

Otimização em Aprendizado de Máquina


  • Modelos de aprendizado de máquina aprendem encontrando parâmetros ótimos (pesos, vieses, etc.).
  • “Ótimo” significa parâmetros que minimizam (ou maximizam) uma função objetivo (ex: função de perda, verossimilhança).
  • Treinamento = Problema de Otimização: Encontrar os valores dos parâmetros \(\boldsymbol{\theta}\) que minimizam uma perda \(L(\boldsymbol{\theta})\).


Objetivo: Dada uma função objetivo, encontrar o melhor conjunto de parâmetros.

Otimização Contínua vs. Discreta


  • Otimização Contínua: Os parâmetros vivem em um espaço contínuo (ex: \(\mathbb{R}^p\)). Este é o foco de hoje.
    • Exemplos: Parâmetros de Regressão Linear.
    • Frequentemente lidamos com funções objetivo diferenciáveis.
  • Otimização Discreta/Combinatória: Parâmetros ou decisões vêm de um conjunto discreto.
    • Exemplos: Seleção de características, encontrar o melhor caminho (problemas de grafos).
    • Usa técnicas diferentes (ex: algoritmos de busca, programação inteira).

Foco: Funções objetivo contínuas e diferenciáveis.

O Cenário: Funções Objetivo



Imagine a função objetivo \(f(\boldsymbol{\theta})\) como uma paisagem sobre o espaço de parâmetros \(\boldsymbol{\Theta}\).


  • Objetivo: Encontrar o ponto mais baixo (valor mínimo).


  • Gradientes (\(\nabla f\)): Apontam para cima na direção de maior crescimento.


  • Intuição: Para encontrar um vale, mova-se na direção oposta do gradiente (para baixo).

Exemplo: Uma Função 1D

Exemplo de função objetivo
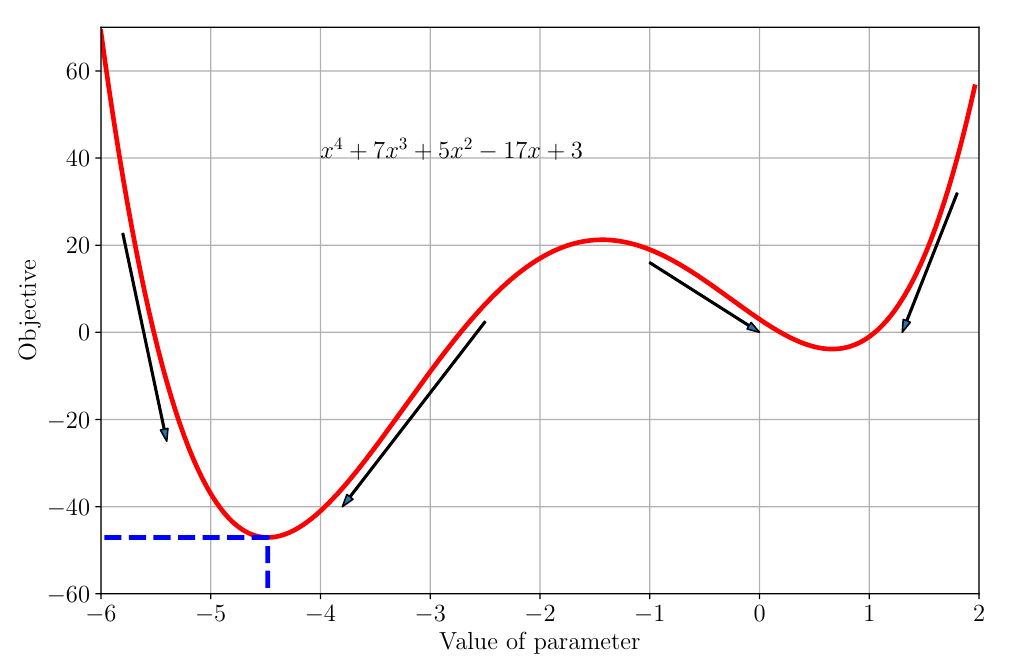
  • Função: \(f(\theta) = \theta^4 + 7\theta^3 + 5\theta^2 - 17\theta + 3\)
  • Mínimo Global: O ponto mais baixo de todos (ao redor de \(\theta \approx -4.5\)).
  • Mínimo Local: O ponto mais baixo em sua vizinhança (ao redor de \(\theta \approx 0.7\)).
  • Gradientes: As setas indicam o gradiente negativo (direção de descida).

Encontrando Mínimos Analiticamente

  • Pontos Estacionários: Pontos onde o gradiente (derivada em 1D) é zero.
    • \(\frac{dl(\theta)}{d\theta} = 4\theta^3 + 21\theta^2 + 10\theta - 17\)
    • Definir \(\frac{dl(\theta)}{d\theta} = 0\) nos dá potenciais mínimos, máximos ou pontos de sela.
  • Teste da Segunda Derivada:
    • \(\frac{d^2l(\theta)}{d\theta^2} = 12\theta^2 + 42\theta + 10\)
    • Se \(\frac{d^2l}{d\theta^2} > 0\) em um ponto estacionário \(\implies\) Mínimo Local.
    • Se \(\frac{d^2l}{d\theta^2} < 0\) em um ponto estacionário \(\implies\) Máximo Local.
    • Se \(\frac{d^2l}{d\theta^2} = 0 \implies\) Inconclusivo.

Encontrando Mínimos Analiticamente



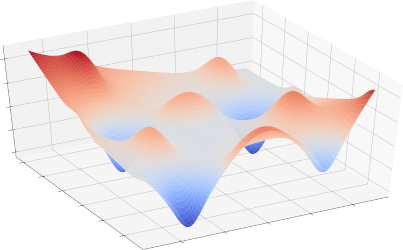
Desafio: Resolver analiticamente \(\nabla f(\boldsymbol{\theta}) = \mathbf{0}\) é frequentemente impossível para modelos complexos de AM.

Encontrando Mínimos Analiticamente



Otimização Numérica:

A Necessidade de Iteração



Como geralmente não podemos resolver para o mínimo diretamente, usamos métodos iterativos.

  1. Comece com uma estimativa inicial \(\boldsymbol{\theta}_0\).
  2. Atualize repetidamente a estimativa para se mover em direção a valores mais baixos da função.


Ideia Chave: Use o gradiente para guiar as atualizações.

Otimização Contínua


  • Gradiente Descendente;
    • Gradiente Descendente com Momento;
    • Gradiente Descendente Estocástico;


  • Otimização com Restrições;
    • Multiplicadores de Lagrange;

Otimização

Gradiente Descendente


Queremos encontrar o mínimo de uma função \(f(\boldsymbol{\theta})\) onde \(\boldsymbol{\theta} \in \mathbb{R}^p\), ou seja, encontrar \[\min_{\boldsymbol{\theta} \in \mathbb{R}^p} f(\boldsymbol{\theta})\] onde \(f\) é diferenciável.


  • O gradiente descendente é um algoritmo de otimização de primeira ordem.

  • Para encontrar um mínimo local de uma função usando o gradiente descendente, damos passos proporcionais ao negativo do gradiente da função no ponto atual.

    • O gradiente \(\nabla f(\boldsymbol{\theta})\) aponta na direção de maior crescimento.
    • O gradiente negativo \(-\nabla f(\boldsymbol{\theta})\) aponta na direção de maior decrescimento.

Otimização

Gradiente Descendente

  • Algoritmo:

    • Comece em \(\boldsymbol{\theta}_0\).
    • mas, no caso geral, itere: \[ \boldsymbol{\theta}_{i+1} = \boldsymbol{\theta}_i - \gamma_i (\nabla f(\boldsymbol{\theta}_i))^\top \]
    • \(\boldsymbol{\theta}_i\): Estimativa atual do parâmetro.
    • \(\nabla f(\boldsymbol{\theta}_i)\): Gradiente de \(f\) em \(\boldsymbol{\theta}_i\).
    • \(\gamma_i\): Tamanho do passo (ou taxa de aprendizado) na iteração \(i\). Geralmente \(\gamma_i = \gamma > 0\).

Se \(\gamma\) for pequeno o suficiente e \(\gamma_i (\nabla f(\boldsymbol{\theta}_i))^\top \geq 0\), \(f(\boldsymbol{\theta}_{i+1}) \le f(\boldsymbol{\theta}_i)\).

Otimização

Gradiente Descendente


Exemplo:

\[f(\theta) = \theta (\theta - 1)\]

Qual é o valor de \(\theta\) que minimiza esta função?


library(torch)

f <- function(theta) theta * (theta - 1)

X11()
plot(f)
theta <- torch_tensor(0, requires_grad = TRUE)
# gradiente descendente
# x[t+1] = x[t] - gamma * df/dx[t]
optimizier <- optim_sgd(theta, lr = 0.01)
#points(theta, f, col = "red")
for(passo in 2:100) {
  optimizier$zero_grad()
  ftheta <- f(theta)
  ftheta$backward()

  optimizier$step()

  points(theta, ftheta, col = "red")
  Sys.sleep(0.1)
}
# o passo é muito pequeno!
# temos que mudar a "taxa de aprendizado"
theta

Otimização

Gradiente Descendente

Exemplo 2:

Seja \(\theta = (x,y)\), e

\[f(x,y) = (x-2)^2 + (y + 1)^2\]

Otimização

Gradiente Descendente - Exemplo: Função Quadrática 2D

Minimizar \(f(\theta_1, \theta_2) = \frac{1}{2} \begin{bmatrix} \theta_1 \\ \theta_2 \end{bmatrix}^\top \begin{bmatrix} 2 & 1 \\ 1 & 20 \end{bmatrix} \begin{bmatrix} \theta_1 \\ \theta_2 \end{bmatrix} - \begin{bmatrix} 5 \\ 3 \end{bmatrix}^\top \begin{bmatrix} \theta_1 \\ \theta_2 \end{bmatrix}\)

Gradiente: \(\nabla f(\theta_1, \theta_2) = \begin{bmatrix} \theta_1 \\ \theta_2 \end{bmatrix}^\top \begin{bmatrix} 2 & 1 \\ 1 & 20 \end{bmatrix} - \begin{bmatrix} 5 \\ 3 \end{bmatrix}^\top\)

Regra de Atualização (usando \(\boldsymbol{\theta} = [\theta_1, \theta_2]^\top\)): \[ \boldsymbol{\theta}_{i+1} = \boldsymbol{\theta}_i - \gamma \left( \begin{bmatrix} 2 & 1 \\ 1 & 20 \end{bmatrix} \boldsymbol{\theta}_i - \begin{bmatrix} 5 \\ 3 \end{bmatrix} \right) \]


(Nota: Usamos a forma de vetor coluna aqui para o cálculo)

Otimização

Gradiente Descendente - Exemplo: Função Quadrática 2D

  • Comece em \(\boldsymbol{\theta}_0 = [-3, -1]^\top\). Tamanho do passo \(\gamma = 0.085\).
  • Qual é o valor de \(\boldsymbol{\theta}_1\)?

\[ \boldsymbol{\theta}_{1} = \begin{bmatrix} -3 \\ -1 \end{bmatrix} - 0.085 \left( \begin{bmatrix} 2 & 1 \\ 1 & 20 \end{bmatrix} \begin{bmatrix} -3 \\ -1 \end{bmatrix} - \begin{bmatrix} 5 \\ 3 \end{bmatrix} \right) \]

\[ \boldsymbol{\theta}_{1} = \begin{bmatrix} -3 \\ -1 \end{bmatrix} - 0.085 \left( \begin{bmatrix} -7 \\ -23 \end{bmatrix} - \begin{bmatrix} 5 \\ 3 \end{bmatrix} \right) \]

\[ \boldsymbol{\theta}_{1} = \begin{bmatrix} -3 \\ -1 \end{bmatrix} - 0.085 \left( \begin{bmatrix} -12 \\ -26 \end{bmatrix} \right) \]

Otimização

Gradiente Descendente - Exemplo: Função Quadrática 2D


\[ \boldsymbol{\theta}_{1} = \begin{bmatrix} -3 \\ -1 \end{bmatrix} - \begin{bmatrix} - 1.02 \\ -2.21 \end{bmatrix} \]



\[ \boldsymbol{\theta}_{1} = \begin{bmatrix} -1.98 \\ 1.21 \end{bmatrix} \]

Otimização

Gradiente Descendente - Exemplo: Função Quadrática 2D

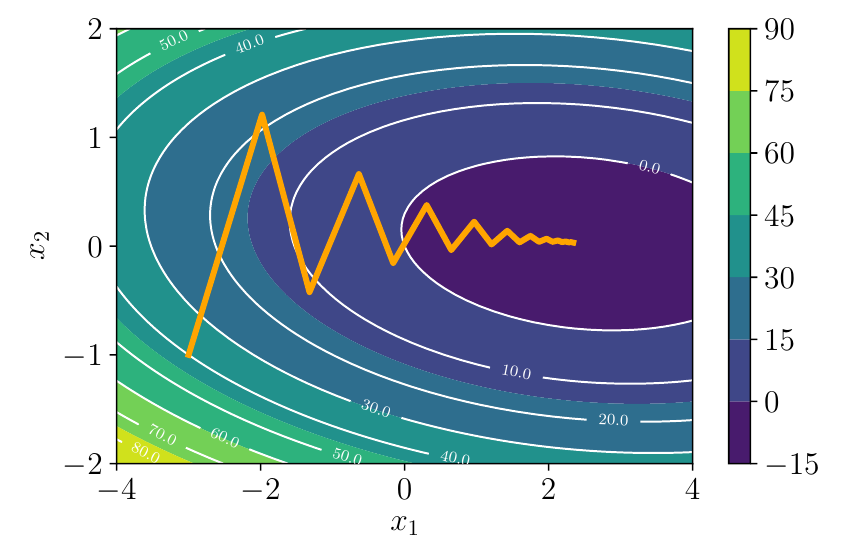
Gradiente Descendente em Superfície Quadrática

Otimização

Gradiente Descendente - Exemplo: Função Quadrática 2D

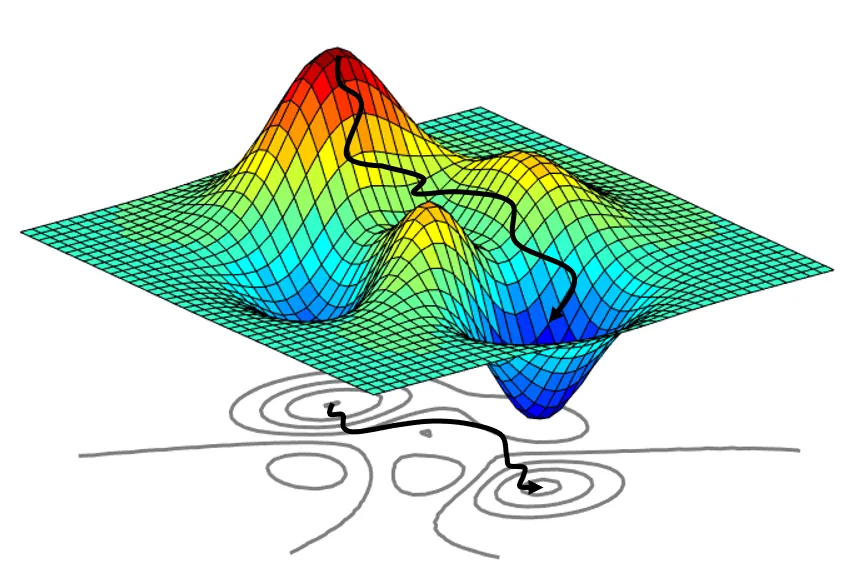
O Tamanho do Passo (\(\gamma\))


  • Também chamado de taxa de aprendizado.

  • \(\gamma\) Muito Pequeno: Convergência muito lenta. Muitos passos são necessários.

  • \(\gamma\) Muito Grande: Ultrapassa o mínimo, oscilações, divergência (o valor da função aumenta).

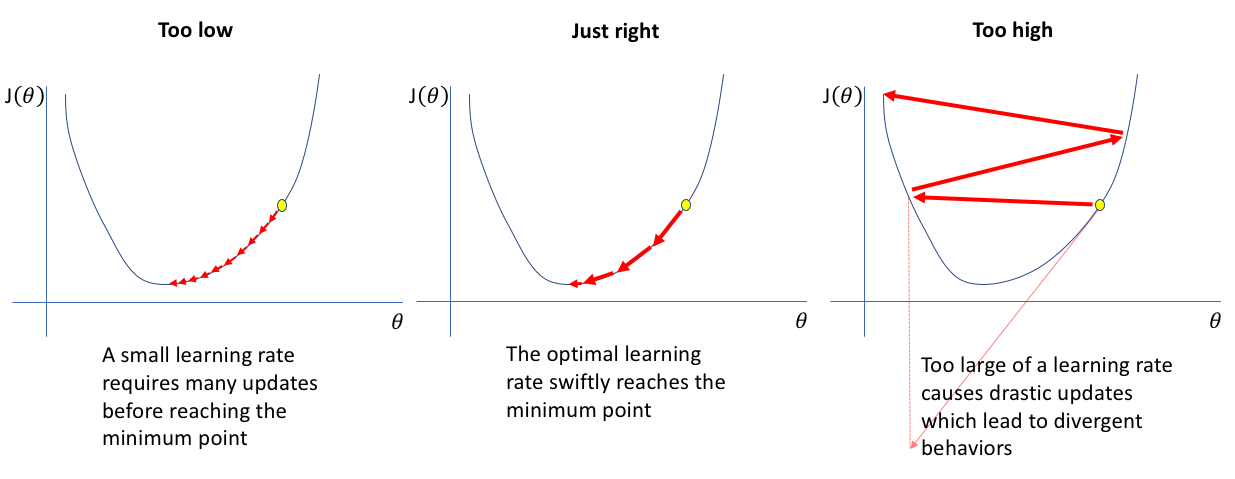
Efeito da taxa de aprendizado - https://www.jeremyjordan.me

O Tamanho do Passo (\(\gamma\))

Escolhendo o Tamanho do Passo


  • \(\gamma\) Fixo: Abordagem mais simples, requer ajuste.
  • \(\gamma\) Decrescente: Comece maior, diminua ao longo do tempo (ex: \(\gamma_i = \gamma_0 / (1+ki)\)). Comum em aprendizado profundo.
  • Métodos Adaptativos: Ajustam \(\gamma\) com base no progresso da otimização.
    • Heurística:
      • Se \(f(\boldsymbol{\theta}_{i+1}) > f(\boldsymbol{\theta}_i)\) (valor aumentou): Desfaça o passo, diminua \(\gamma\).
      • Se \(f(\boldsymbol{\theta}_{i+1}) < f(\boldsymbol{\theta}_i)\) (valor diminuiu): Talvez aumente \(\gamma\).
    • Existem métodos mais sofisticados (AdaGrad, RMSProp, Adam - além deste capítulo).
  • Busca em Linha: Encontre o \(\gamma_i\) ótimo em cada passo que minimiza \(f(\boldsymbol{\theta}_i - \gamma \nabla f(\boldsymbol{\theta}_i))\) ao longo da direção do gradiente. Pode ser custoso.





Gradiente Descendente com Momento

Gradiente Descendente com Momento

  • Ideia: Introduzir um termo de “velocidade” \(\Delta \boldsymbol{\theta}_i\) que acumula gradientes passados. A atualização depende do gradiente atual e da direção anterior.
  • Regras de Atualização: \[ \Delta \boldsymbol{\theta}_{i+1} = \alpha \Delta \boldsymbol{\theta}_i - \gamma (\nabla f(\boldsymbol{\theta}_i))^\top \quad (\text{Atualização da velocidade}) \] \[ \boldsymbol{\theta}_{i+1} = \boldsymbol{\theta}_i + \Delta \boldsymbol{\theta}_{i+1} \quad (\text{Atualização da posição}) \]
    • \(\alpha \in [0,1]\): Parâmetro de momento (ex: 0.9), fator de decaimento para a velocidade passada.
    • \(\Delta \boldsymbol{\theta}_i\): Mudança em \(\boldsymbol{\theta}\) do passo \(i-1\) para \(i\), ou seja, \[\Delta \boldsymbol{\theta}_i = \boldsymbol{\theta}_i - \boldsymbol{\theta}_{i-1} = \alpha \Delta \boldsymbol{\theta}_{i-1} - \gamma (\nabla f(\boldsymbol{\theta}_{i-1}))^\top\]

Um α mais alto dá mais importância ao passado, preservando mais da velocidade anterior nas atualizações.

Momento: Intuição


  • Como uma bola pesada rolando morro abaixo.
  • Acumula velocidade em direções consistentes de descida.
  • Faz a média dos componentes oscilantes do gradiente.
  • Ajuda a passar por pequenos mínimos locais ou regiões planas.

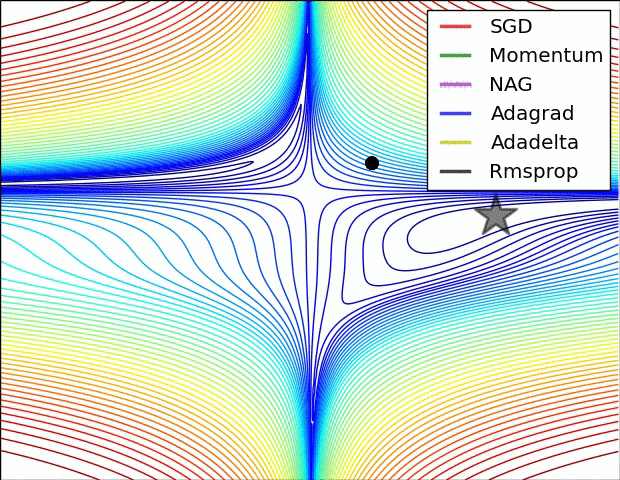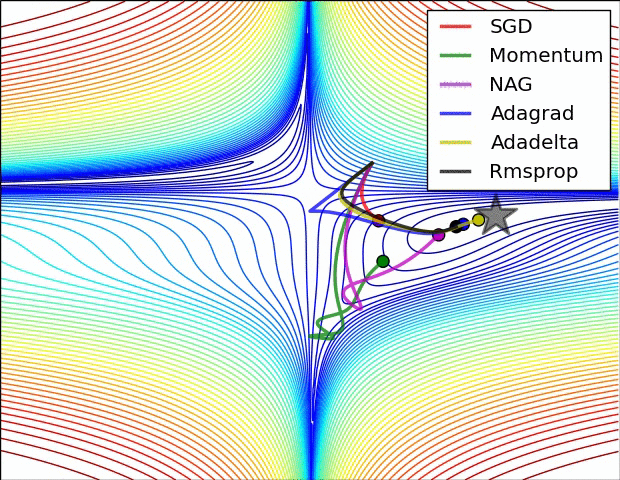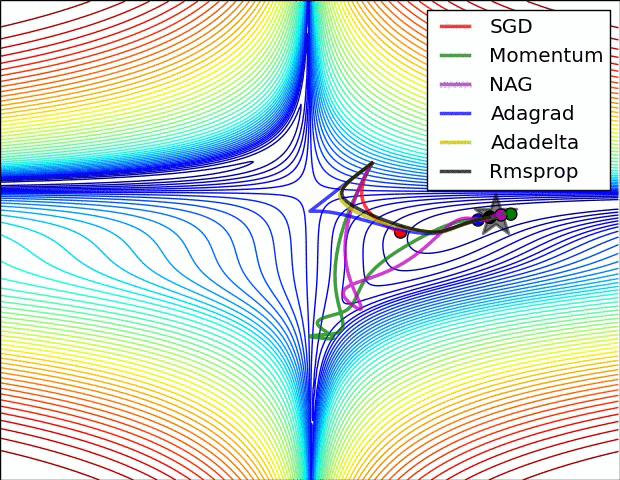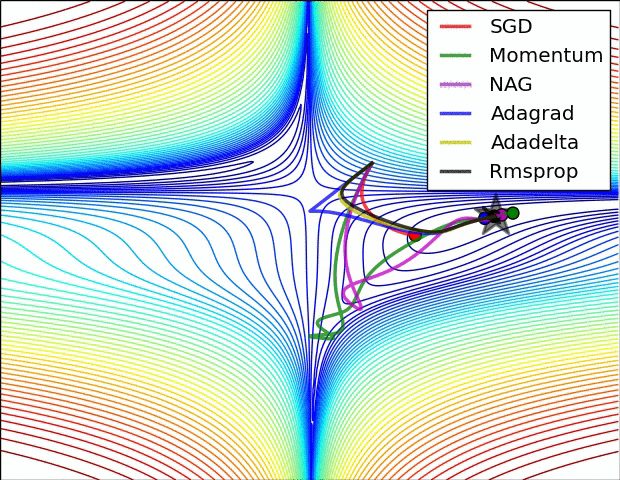
Momento vs GD - https://cs231n.github.io/neural-networks-3/

Custo Computacional


  • A função objetivo em AM é frequentemente uma soma sobre n pontos de dados: \[ \mathcal{L}(\boldsymbol{\theta}) = \frac{1}{n} \sum_{i=1}^n \mathcal{L}_i(\boldsymbol{\theta})\]
    • \(\mathcal{L}_i(\boldsymbol{\theta})\): Perda para o \(i\)-ésimo ponto de dados \((\boldsymbol{\theta}_i, y_i)\).
  • O gradiente também é uma soma: \[ \nabla \mathcal{L}(\boldsymbol{\theta}) = \frac{1}{n} \sum_{i=1}^n \nabla \mathcal{L}_i(\boldsymbol{\theta}) \]
  • Calcular o gradiente completo requer a iteração por todo o conjunto de dados a cada passo.
  • Impraticável para grandes conjuntos de dados (ex: milhões de imagens).





Gradiente Descendente Estocástico (SGD)

Gradiente Descendente Estocástico (SGD)

  • Ideia: Aproximar o gradiente completo usando apenas um ou um pequeno lote de pontos de dados a cada passo.
  • SGD de Ponto Único:
    1. Escolha um ponto de dados aleatório \(i\) de \(\{1, \ldots, n\}\).
    2. Atualize usando apenas o gradiente para aquele ponto: \[ \boldsymbol{\theta}_{i+1} = \boldsymbol{\theta}_i - \gamma_i (\nabla \mathcal{L}_i(\boldsymbol{\theta}_i))^\top \]
  • SGD de Mini-lote (Mais Comum):
    1. Escolha um mini-lote aleatório \(\mathcal{B}\) de tamanho \(B\) (ex: \(B=32, 64, \ldots\)) de \(\{1, \ldots, n\}\).
    2. Atualize usando o gradiente médio sobre o mini-lote: \[ \boldsymbol{\theta}_{i+1} = \boldsymbol{\theta}_i - \gamma_i \left( \frac{1}{B} \sum_{i \in \mathcal{B}} \nabla \mathcal{L}_i(\boldsymbol{\theta}_i) \right)^\top \]

SGD: Por Que Funciona?

  • Em média, o gradiente estocástico aponta na mesma direção do gradiente verdadeiro.
  • Atualizações muito mais rápidas: O custo por passo é proporcional a \(B\), não a \(n\).
  • Gradientes Ruidosos: O caminho percorrido é muito mais ruidoso do que o GD de lote completo.

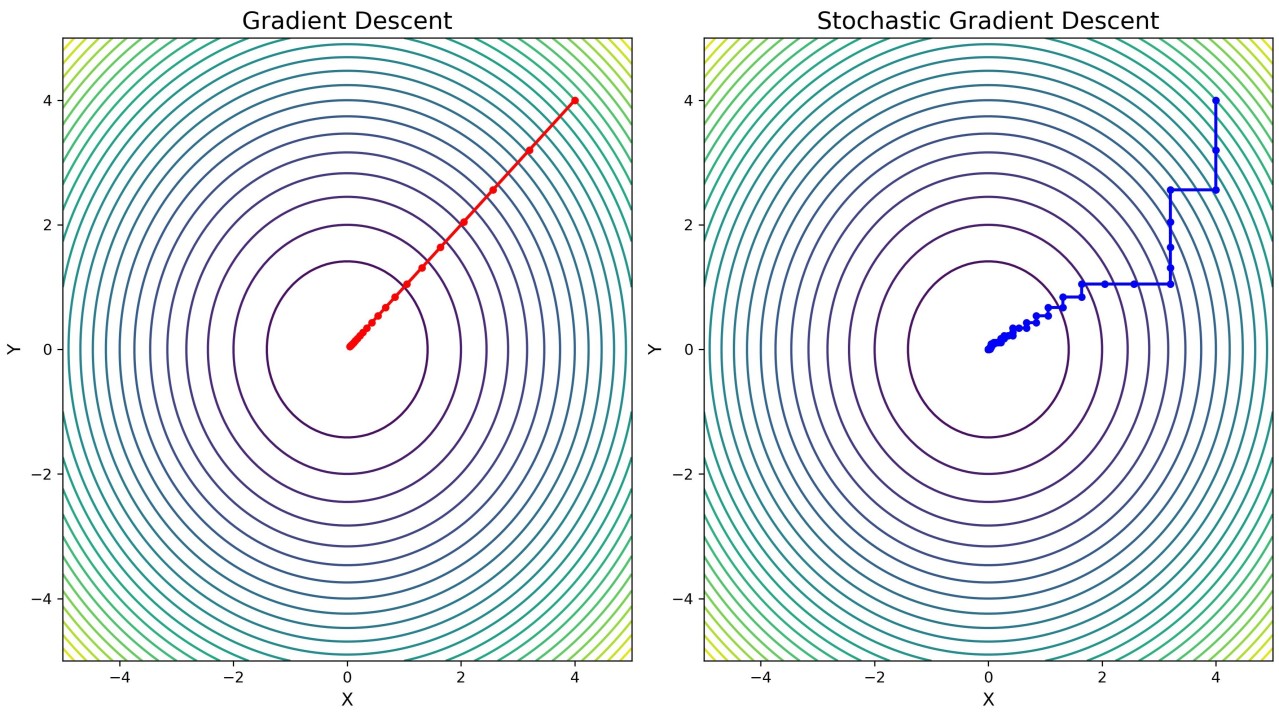
Caminho do SGD vs GD - pulse/gradient-descent-gd-stochastic-sgd-vekil-bekmyradov-qvs4e/

SGD: Prós e Contras

Prós:

  • Computacionalmente eficiente: Escala para conjuntos de dados massivos.
  • Progresso inicial mais rápido: Pode fazer atualizações com mais frequência.
  • O ruído pode ajudar a escapar de mínimos locais: A aleatoriedade pode tirar os parâmetros de ótimos locais rasos.
  • Muitas vezes leva a uma melhor generalização (desempenho em dados não vistos), talvez porque encontre mínimos “mais planos”.

Contras:

  • Atualizações ruidosas: A convergência pode ser errática, pode não se estabilizar precisamente no mínimo. Requer ajuste cuidadoso do cronograma da taxa de aprendizado (diminuindo \(\gamma\)).
  • Maior variância nas atualizações dos parâmetros em comparação com o GD em lote. O tamanho do mini-lote \(B\) controla essa troca.

Conclusão


  • A otimização contínua fornece o motor para treinar muitos modelos de aprendizado de máquina.


  • O Gradiente Descendente e suas variantes estocásticas são as ferramentas principais, especialmente para problemas de grande escala.

Referências


Básicas

  • Aprendizado de Máquina: uma abordagem estatística, Izibicki, R. and Santos, T. M., 2020, link: https://rafaelizbicki.com/AME.pdf.

  • An Introduction to Statistical Learning: with Applications in R, James, G., Witten, D., Hastie, T. and Tibshirani, R., Springer, 2013, link: https://www.statlearning.com/.

  • Mathematics for Machine Learning, Deisenroth, M. P., Faisal. A. F., Ong, C. S., Cambridge University Press, 2020, link: https://mml-book.com.

Referências


Complementares

  • An Introduction to Statistical Learning: with Applications in python, James, G., Witten, D., Hastie, T. and Tibshirani, R., Taylor, J., Springer, 2023, link: https://www.statlearning.com/.

  • Matrix Calculus (for Machine Learning and Beyond), Paige Bright, Alan Edelman, Steven G. Johnson, 2025, link: https://arxiv.org/abs/2501.14787.

  • Machine Learning Beyond Point Predictions: Uncertainty Quantification, Izibicki, R., 2025, link: https://rafaelizbicki.com/UQ4ML.pdf.

  • Mathematics of Machine Learning, Petersen, P. C., 2022, link: http://www.pc-petersen.eu/ML_Lecture.pdf.