Introdução à Ciência de Dados
k-NN e SVM
UFPE
Notação
Nesse slide será detalhado algumas notações que utilizaremos ao longo do curso:
- \(x \,\, \rightarrow\) representa um escalar, ou seja, um valor único que pode representar um valor quantitativo ou qualitativo;
- \(\mathbf{x} \,\, \rightarrow\) representa um vetor de valores, estes podem ser valores quantitativos ou qualitativos; Vetores são representados por um conjunto de escalares.
- \(\mathbf{X} \,\, \rightarrow\) representa matrizes, estas podem ser formadas por vetores, e escalares.
Classificação
Seja \(\mathbf{X}\) uma matriz de dados, ou base de dados conhecida, com \(n\) observações (linhas) e \(p\) variáveis (colunas), e \(\mathbf{y}\) um outro vetor de observações,
\[\mathbf{X} = [\mathbf{x}_1, \ldots, \mathbf{x}_n]^\top = \begin{bmatrix} x_{11} & \cdots & x_{1p} \\ \vdots & \ddots & \vdots \\ x_{n1} & \cdots & x_{np} \end{bmatrix} \quad \text{e} \quad \mathbf{y} = [y_1, \ldots, y_n]^\top,\]
- Em problemas de classificação, o vetor \(\mathbf{y}\) é chamado de variável resposta, label, variável dependente, e cada observação \(y_1 , \ldots , y_n\) é do tipo qualitativa.
- Formalmente, no exemplo de um caso de \(c\) classes, é utilizado o par \((\mathbf{x}, y)\), com \(\mathbf{x} \in \mathbb{R}^p\) e \(y \in \mathbb{N}\), em que \(y \in \{1, \ldots , c \}\).
- Dessa forma, um classificador será sempre uma função \(f : \mathbb{R}^p \rightarrow \mathbb{N}\);
SVM - Support Vector Machine
SVM - Support Vector Machine
- O SVM foi proposto incialmente como um algoritmo de classificação binária, mas atualmente pode ser estendido para classificação multiclasse.
- O SVM é um algoritmo de classificação que busca encontrar o hiperplano que melhor separa as classes1.
- Os hiperplanos podem ser nas versões lineares e não lineares.
- O hiperplano é definido como o subespaço de dimensão \(p-1\) em \(\mathbb{R}^p\).
- Por exemplo, em 2 dimensões, tem-se uma reta;
- Em 3 dimensões, um plano;
SVM - Support Vector Machine
Caso Linear
- Será considerado um problema de classificação com duas classes, ou seja, \(y \in \{-1, 1\}\).
- Relembrem que, em um caso de \(c\) classes, teremos o par \((\mathbf{x}, y)\), com \(\mathbf{x} \in \mathbb{R}^p\).
- em que as respostas \(y_1 , \ldots , y_n\) são qualitativas para uma amostra de tamanho \(n\).
- O problema de classificação consiste em encontrar um hiperplano ótimo que separa as classes.
SVM - Support Vector Machine
Caso Linear
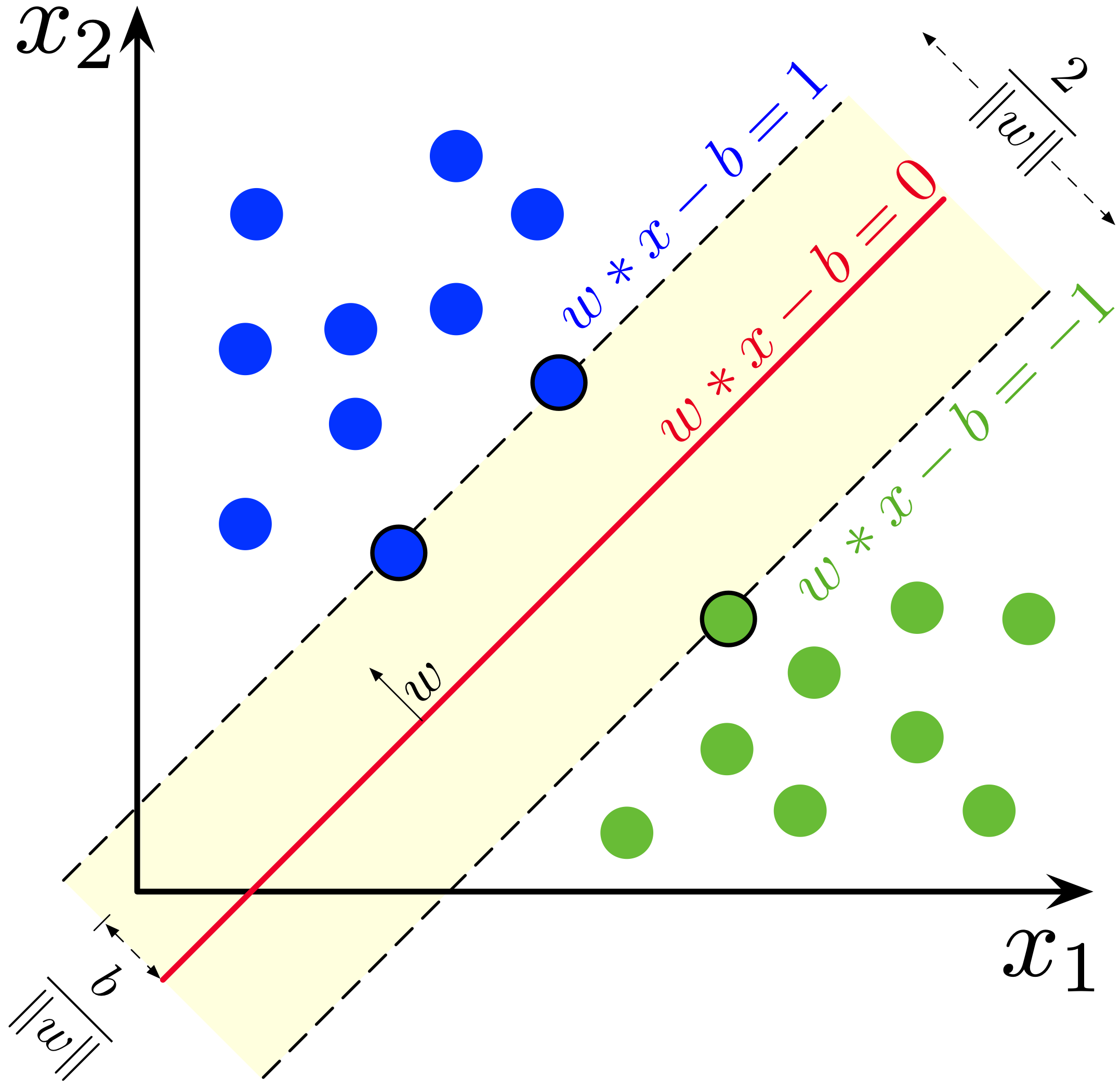
- O hiperplano é definido como:
\[\mathbf{w}^\top \mathbf{x} + b = 0,\]
em que \(\mathbf{w}\) é o vetor normal ao hiperplano e \(b\) é o termo de interceptação.
- A distância entre o hiperplano e o ponto \(\mathbf{x}_i\) é dada por:
\[\frac{|\mathbf{w}^\top \mathbf{x}_i + b|}{||\mathbf{w}||}.\]
- O hiperplano ótimo é aquele que maximiza a margem entre as classes.
SVM - Support Vector Machine
Caso Linear
- A definição de um vetor normal é dado por:
\[\mathbf{w} = \sum_{i=1}^{n} \alpha_i y_i \mathbf{x}_i,\] em que \(\alpha_i\) são os multiplicadores de Lagrange, e \(y_i\) é a classe do vetor \(\mathbf{x}_i\).
- Multiplicadores de Langrange são soluções do problema de otimização:
\[\max_{\alpha} \sum_{i=1}^{n} \alpha_i - \frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n} \alpha_i \alpha_j y_i y_j \mathbf{x}_i^\top \mathbf{x}_j,\]
em que \(\alpha_i \geq 0\) e \(\sum_{i=1}^{n} \alpha_i y_i = 0\).
SVM - Support Vector Machine
Caso Linear
- A distância entre os vetores de suporte e o hiperplano considerado é chamado de margem e é igual a \(2/||\mathbf{w}||\), em que \(||\mathbf{w}|\) é referente a norma do vetor \(\mathbf{w}\).
- A norma do vetor \(\mathbf{w}\) é dada por:
\[||\mathbf{w}|| = \sqrt{\sum_{j=1}^{p} w_j^2}.\]
em que \(w_j\) é o \(j\)-ésimo elemento do vetor \(\mathbf{w}\).
SVM - Support Vector Machine
Caso Linear
- No caso linear a função de classificação é definida como:
\[f(\mathbf{x}) = \mathbf{w}^\top \mathbf{x} + b,\]
em que \(\mathbf{w}\) é o vetor normal ao hiperplano e \(b\) é o termo de interceptação.
- A classe predita é dada por:
\[\hat{y} = \text{sign}(f(\mathbf{x})).\]
em que \(\text{sign}(f(\mathbf{x})) = 1\) se \(f(\mathbf{x}) > 0\) e \(\text{sign}(f(\mathbf{x})) = -1\) se \(f(\mathbf{x}) < 0\). E \(sign\) é definido como a função sinal, ou seja, \(sign(x) = 1\) se \(x > 0\) e \(sign(x) = -1\) se \(x < 0\).
SVM - Support Vector Machine
SVM - Support Vector Machine
Caso Não Linear
SVM - Support Vector Machine
Caso Não Linear
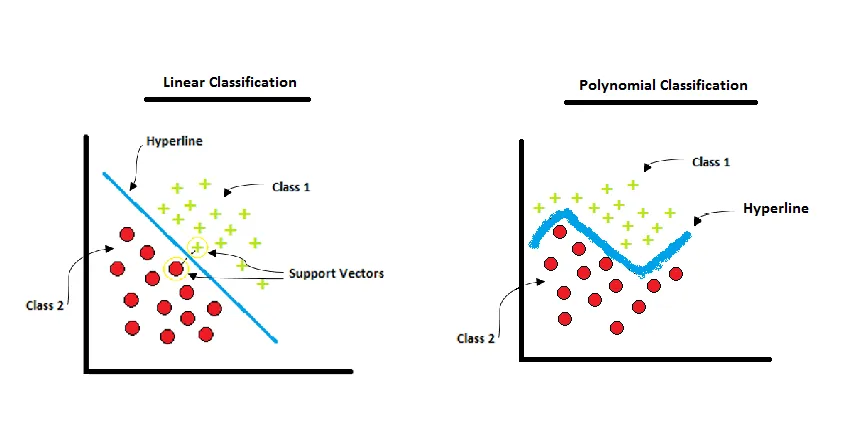
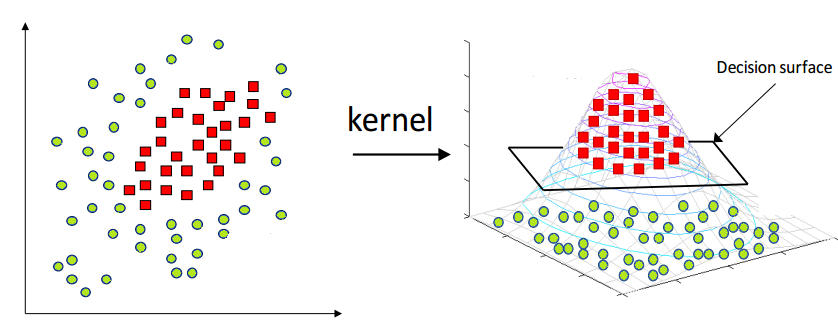
- Em geral não é possível separar as classes linearmente, então é possível mapear os dados levando para um espaço de dimensão superior (fazendo uma projeção), e assim os dados se tornam linearmente separáveis.
- O SVM pode ser estendido para casos não lineares através da utilização de funções kernel.
- As funções kernel são funções que mapeiam os dados para um espaço de dimensão superior.
SVM - Support Vector Machine
SVM - Support Vector Machine
SVM - Support Vector Machine
Caso Não Linear
- A função kernel mais comum é a função kernel polinomial:
\[K(\mathbf{x}_i, \mathbf{x}_j) = (\mathbf{x}_i^\top \mathbf{x}_j + 1)^d,\]
em que \(d\) é a ordem do polinômio.
- Outra função kernel comum é a função kernel radial:
\[K(\mathbf{x}_i, \mathbf{x}_j) = \exp\left(-\gamma ||\mathbf{x}_i - \mathbf{x}_j||^2\right),\]
em que \(\gamma\) é um parâmetro de suavização.
SVM - Support Vector Machine
Caso Não Linear
- Tem a função kernel sigmoide outangente hiperbólica:
\[K(\mathbf{x}_i, \mathbf{x}_j) = \tanh(\kappa \mathbf{x}_i^\top \mathbf{x}_j + \theta),\]
em que \(\kappa\) e \(\theta\) são parâmetros.
- Nesse caso não linear a função de classificação é definido como:
\[f(\mathbf{x}) = \sum_{i \in SV} \alpha_i y_i K(\mathbf{x}_i, \mathbf{x}) + b,\]
em que \(\alpha_i\) são os multiplicadores de Lagrange, \(y_i\) é a classe do vetor \(\mathbf{x}_i\), e \(b\) é o termo de interceptação e \(SV\) são os vetores de suporte.
SVM - Support Vector Machine
Caso Não Linear
- A o valor predito para \(y\) é obtido por:
\[\hat{y} = \text{sign}(f(\mathbf{x})),\] em que \(\text{sign}(f(\mathbf{x})) = 1\) se \(f(\mathbf{x}) > 0\) e \(\text{sign}(f(\mathbf{x})) = -1\) se \(f(\mathbf{x}) < 0\).
- O problema de otimização é dado por:
\[\max_{\alpha} \sum_{i=1}^{n} \alpha_i - \frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n} \alpha_i \alpha_j y_i y_j K(\mathbf{x}_i, \mathbf{x}_j),\]
em que \(\alpha_i \geq 0\) e \(\sum_{i=1}^{n} \alpha_i y_i = 0\).
SVM - Support Vector Machine
- No caso multiclasse, temos as funções de classificação dadas por:
\[f(\mathbf{x}) = \sum_{i \in SV} \sum_{g=1}^{c} \alpha_{ig} y_{ig} \mathbf{x}_i^\top \mathbf{x} + b_g \text{ (caso linear)},\] \[f(\mathbf{x}) = \sum_{i \in SV} \sum_{g=1}^{c} \alpha_{ig} y_{ig} K(\mathbf{x}_i, \mathbf{x}) + b_g \text{ (caso não linear)},\]
em que \(\alpha_{ig}\) são os multiplicadores de Lagrange, \(y_{ig}\) é a classe do vetor \(\mathbf{x}_i\), e \(b_g\) é o termo de interceptação.
SVM - Support Vector Machine
- A classe predita é dada por:
\[\hat{y} = \text{arg max}_g f_g(\mathbf{x}),\]
em que \(f_g(\mathbf{x})\) é a função de classificação para a classe \(g\). Assim, a função de classificação no caso linear para a classe \(g\) como:
\[f_g(\mathbf{x}) = \sum_{i \in SV} \alpha_{ig} y_{ig} \mathbf{x}_i^\top \mathbf{x} + b_g.\]
- e para o caso não linear é dada por:
\[f_g(\mathbf{x}) = \sum_{i \in SV} \alpha_{ig} y_{ig} K(\mathbf{x}_i, \mathbf{x}) + b_g.\]
SVM - Support Vector Machine
Resumo do processo
O problema de otimização da SVM é onde se busca maximizar a seguinte função: \[\max_{\alpha} \sum_{i=1}^{n} \alpha_i - \frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n} \alpha_i \alpha_j y_i y_j \mathbf{x}_i^\top \mathbf{x}_j,\]
Durante a otimização, o algoritmo considera todas as observações da amostra \((\mathbf{x}_i, y_i)\) do conjunto de treinamento. Isso é necessário porque o objetivo é encontrar os multiplicadores de Lagrange \(\alpha_i\) que maximizem a função objetivo sujeita às restrições.
Após resolver o problema de otimização, os valores dos multiplicadores de Lagrange \(\alpha_i\) são determinados. Em seguida, identifica-se quais observações foram determinadas com \(\alpha_i > 0\). Essas observações serão os vetores de suporte.
SVM - Support Vector Machine
Resumo do processo
Os vetores de suporte são as observações do conjunto de treinamento que têm um impacto direto na definição do hiperplano de separação. Uma vez identificados, apenas esses vetores de suporte são usados para definir a função de decisão da SVM.
No modelo final da SVM, a função de decisão usa apenas os vetores de suporte para tomar a decisão.
Para o caso linear, a função de decisão \(f_g(\mathbf{x})\) é dada por:
\[ f_g(\mathbf{x}) = \sum_{i \in \text{SV}} \alpha_{ig} y_{ig} \mathbf{x}_i^\top \mathbf{x} + b_g, \]
onde \(\mathbf{x}_i\) são os vetores de suport, \(\mathbf{x}\) é um novo vetor de entrada, \(\alpha_{ig}\) são os multiplicadores de Lagrange para a classe \(g\) associados aos vetores de suporte, \(y_{ig}\) é o rótulo da classe \(g\) para o \(i\)-ésimo vetor de suporte, e \(b_g\) é o termo de bias para a classe \(g\).
SVM - Support Vector Machine
Resumo do processo
Para o caso não linear, a função de decisão \(f_g(\mathbf{x})\) usando um kernel \(K(\mathbf{x}_i, \mathbf{x})\) é dada por:
\[ f_g(\mathbf{x}) = \sum_{i \in \text{SV}} \alpha_{ig} y_{ig} K(\mathbf{x}_i, \mathbf{x}) + b_g, \]
onde \(\mathbf{x}_i\) são os vetores de suporte, \(\mathbf{x}\) é um novo vetor de entrada, \(\alpha_{ig}\) são os multiplicadores de Lagrange para a classe \(g\) associados aos vetores de suporte, \(y_{ig}\) é o rótulo da classe \(g\) para o \(i\)-ésimo vetor de suporte, \(b_g\) é o termo de viés para a classe \(g\) e \(K(\mathbf{x}_i, \mathbf{x})\) é a função kernel que calcula a similaridade entre \(\mathbf{x}_i\) e \(\mathbf{x}\).
Referências para serem utilizadas
Estatística e ciência de dados., Morettin, Pedro Alberto, and Júlio da Motta Singer, 2022.
An Introduction to Statistical Learning: With Applications in R, James, G., Witten, D., Hastie, T. and Tibshirani, R., Springer-Verlag, 2013.
Aprendizado de máquina: uma abordagem estatística, Izbicki, R. and Santos, T. M., 2020.
Extras:
https://towardsdatascience.com/support-vector-machine-svm-and-the-multi-dimensional-wizardry-b1563ccbc127
https://pub.towardsai.net/fully-explained-svm-classification-with-python-eda124997bcd
OBRIGADO!
Slide produzido com quarto
Introdução à Ciência de Dados - Prof. Jodavid Ferreira