Introdução à Ciência de Dados
k-NN
UFPE
Notação
Nesse slide será detalhado algumas notações que utilizaremos ao longo do curso:
- \(x \,\, \rightarrow\) representa um escalar, ou seja, um valor único que pode representar um valor quantitativo ou qualitativo;
- \(\mathbf{x} \,\, \rightarrow\) representa um vetor de valores, estes podem ser valores quantitativos ou qualitativos; Vetores são representados por um conjunto de escalares.
- \(\mathbf{X} \,\, \rightarrow\) representa matrizes, estas podem ser formadas por vetores, e escalares.
Classificação
Seja \(\mathbf{X}\) uma matriz de dados, ou base de dados conhecida, com \(n\) observações (linhas) e \(p\) variáveis (colunas), e \(\mathbf{y}\) um outro vetor de observações,
\[\mathbf{X} = [\mathbf{x}_1, \ldots, \mathbf{x}_n]^\top = \begin{bmatrix} x_{11} & \cdots & x_{1p} \\ \vdots & \ddots & \vdots \\ x_{n1} & \cdots & x_{np} \end{bmatrix} \quad \text{e} \quad \mathbf{y} = [y_1, \ldots, y_n]^\top,\]
- Em problemas de classificação, o vetor \(\mathbf{y}\) é chamado de variável resposta, label, variável dependente, e cada observação \(y_1 , \ldots , y_n\) é do tipo qualitativa.
- Formalmente, no exemplo de um caso de \(c\) classes, é utilizado o par \((\mathbf{x}, y)\), com \(\mathbf{x} \in \mathbb{R}^p\) e \(y \in \mathbb{N}\), em que \(y \in \{1, \ldots , c \}\).
- Dessa forma, um classificador será sempre uma função \(f : \mathbb{R}^p \rightarrow \mathbb{N}\);
k-NN
Algoritmo k-NN
- O algoritmo k vizinhos mais próximos (k-NN - k-Nearest Neighbors) é uma extensão do algoritmo NN e foi proposta por Cover e Hart.
- Estes são considerado o algoritmo um dos mais simples de classificação;
- Possuem várias propostas diferentes e podem ser competitivos em comparação com outros métodos mesmo com suas simplicidades.
Algoritmo k-NN
- Relembrem que, em um caso de classificação de \(c\) classes, teremos o par \((\mathbf{x}, y)\), com \(\mathbf{x} \in \mathbb{R}^p\) e \(y \in \{1, \ldots , c \}\), em que as respostas \(y_1 , \ldots , y_n\) são qualitativas.
- e um classificador será sempre uma função \(f : \mathbb{R}^p \rightarrow \mathbb{N}\);
- em que
\[\hat{y} = f(\mathbf{x}),\]
sendo \(\mathbf{x} = [x_1, \ldots, x_p]^\top\).
Algoritmo k-NN
Seja \(\mathbf{X}\) uma matriz de dados de treinamento, ou base de dados conhecida, com \(n\) observações (linhas) e \(p\) variáveis (colunas), e \(\mathbf{y}\) um outro vetor de observações, nesse caso, variável resposta,
\[\mathbf{X} = [\mathbf{x}_1, \ldots, \mathbf{x}_n]^\top = \begin{bmatrix} x_{11} & \cdots & x_{1p} \\ \vdots & \ddots & \vdots \\ x_{n1} & \cdots & x_{np} \end{bmatrix} \quad \text{e} \quad \mathbf{y} = [y_1, \ldots, y_n]^\top,\]
e seja \((\mathbf{x}_0, y_0)\) um par de dados de teste, sendo \(\mathbf{x}_0\) as informações das \(p\) variáveis e \(y_0\) a resposta conhecida.
Algoritmo k-NN
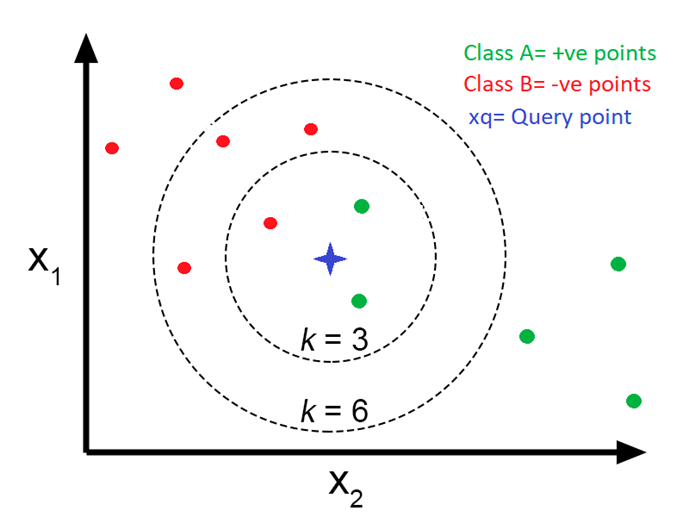
então, temos que a classe predita da observação \(\mathbf{x}_0\) é definida pelo algoritmo k-NN, como:
\[\hat{y} = \underset{i \in \mathcal{N}_{\mathbf{x_0}}}{\text{moda }} y_{i},\]
em que, \(\mathcal{N}_{\mathbf{x_0}}\) é o conjunto das \(k\) observações mais próximas de \(\mathbf{x}_0\). Podemos também escrever em termos de probabilidade:
\[\hat{y} = \underset{y}{\text{arg max }} P(f(\mathbf{x_0}) = y)=\frac{1}{k} \sum_{i \in k} I(y_i = y),\]
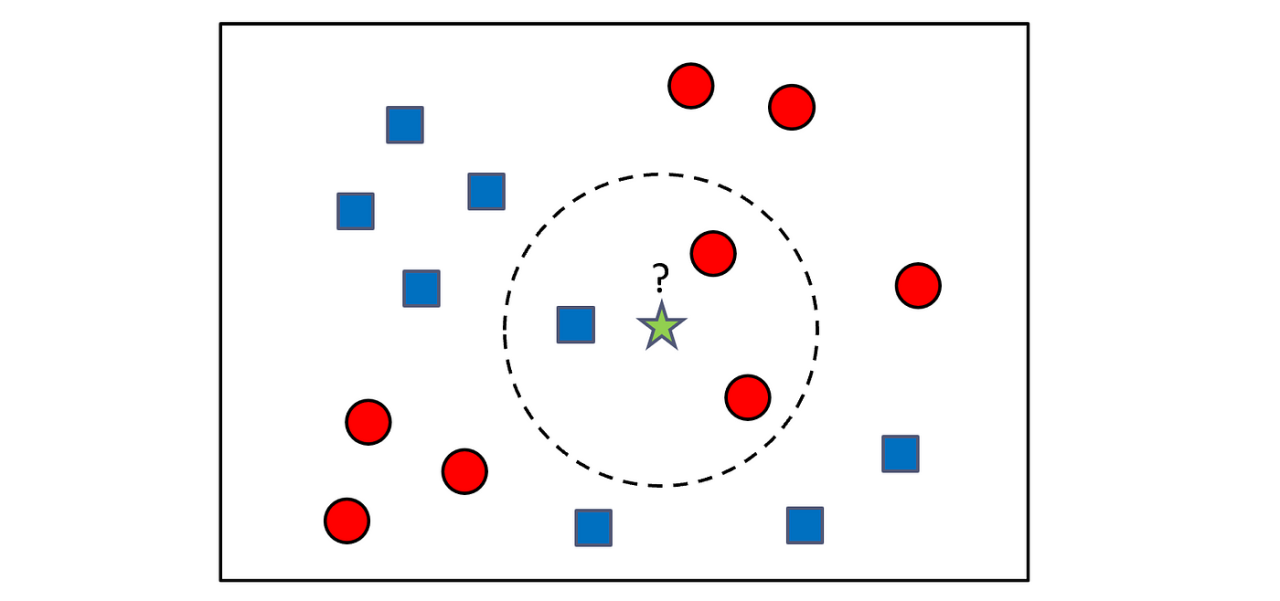
E como encontramos as k observações mais próximas de \(\mathbf{x_0}\)?
Algoritmo k-NN
- O algoritmo k-NN seleciona os \(k\) vizinhos mais próximos através de distâncias entre os valores das observações de treinamento com a observação de teste.
- Uma distância, é uma função que mede a dissimilaridade entre duas observações e possui algumas propriedades.
Suponha dois vetores \(\mathbf{x}_i\) e \(\mathbf{x}_j\) qualquer, temos que a distância \(d(\mathbf{x}_i, \mathbf{x}_j)\) deve satisfazer as seguintes propriedades:
\(d(\mathbf{x}_i, \mathbf{x}_j) \geq 0\) para todo \(i\) e \(j\);
\(d(\mathbf{x}_i, \mathbf{x}_j) = 0\) se, e somente se, \(\mathbf{x}_i = \mathbf{x}_j\);
\(d(\mathbf{x}_i, \mathbf{x}_j) = d(\mathbf{x}_j, \mathbf{x}_i)\);
\(d(\mathbf{x}_i, \mathbf{x}_j) \leq d(\mathbf{x}_i, \mathbf{x}_k) + d(\mathbf{x}_k, \mathbf{x}_j)\), dado um terceiro vetor \(\mathbf{x}_k\) (desigualdade triangular).
Algoritmo k-NN
- As distâncias mais comuns são a distância euclidiana e a distância de Mahalanobis.
A distância euclidiana entre dois vetores \(\mathbf{x}_i\) e \(\mathbf{x}_j\) é dada por:
\[d(\mathbf{x}_i, \mathbf{x}_j) = \sqrt{\sum_{l=1}^{p} (x_{il} - x_{jl})^2}.\]
Algoritmo k-NN
A distância de Mahalanobis é dada por:
\[d(\mathbf{x}_i, \mathbf{x}_j) = \sqrt{(\mathbf{x}_i - \mathbf{x}_j)^\top \mathbf{S}^{-1} (\mathbf{x}_i - \mathbf{x}_j)},\] em que, \(\mathbf{S}\) é a matriz de covariância dos dados de treinamento.
Algoritmo k-NN
Alguns pontos importantes:
- Como o algoritmo \(k\)-NN utiliza distâncias, isso coloca um pressuposto de que todas as variáveis (features) devem ser numéricas.
- Outro ponto importante, é que a distância euclidiana é sensível à escala das variáveis, então é interessante padronizar as variáveis.
- A distância de Mahalanobis é uma alternativa para variáveis correlacionadas.
Algoritmo k-NN

Algoritmo k-NN

Algoritmo k-NN
Algoritmo k-NN
Referências para serem utilizadas
Estatística e ciência de dados., Morettin, Pedro Alberto, and Júlio da Motta Singer, 2022.
An Introduction to Statistical Learning: With Applications in R, James, G., Witten, D., Hastie, T. and Tibshirani, R., Springer-Verlag, 2013.
Aprendizado de máquina: uma abordagem estatística, Izbicki, R. and Santos, T. M., 2020.
Extras:
https://towardsdatascience.com/support-vector-machine-svm-and-the-multi-dimensional-wizardry-b1563ccbc127
https://pub.towardsai.net/fully-explained-svm-classification-with-python-eda124997bcd
OBRIGADO!
Slide produzido com quarto
Introdução à Ciência de Dados - Prof. Jodavid Ferreira