Tópicos Especiais em Estatística Comp.
Redes Neurais Convolucionais
UFPE
Introdução
- A visão humana é um processo complexo que envolve a captura de luz, processamento e interpretação de sinais visuais.
- Compreender como a visão humana funciona pode nos ajudar a entender e desenvolver redes neurais convolucionais (CNNs).
Introdução
Como funciona a visão?
a luz entra em seus olhos, a córnea a refrata e ela penetra passando pela pupila e sendo focada pelo cristalino (lentes) na segunda parte do olho, onde encontra a retina.
Onde células fotossensíveis iniciam sua transformação em sinais elétricos que a transformarão em visão.
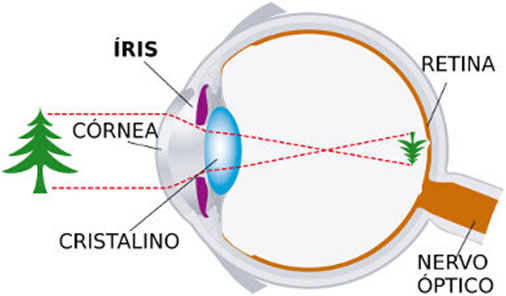
Olho Humano. Fonte: https://www.hospitalvisaosc.com.br/artigo/11/como-funciona-o-olho-humano-?
Introdução
Olho humano
- Córnea: Primeira lente que refrata a luz.
- Cristalino: Ajusta o foco da luz na retina.
- Retina: Camada de células sensíveis à luz (fotorreceptores), em média composta de cerca de 120 milhões de bastonetes e 6 milhões de cones (sensores), converte o estímulo luminoso em sinais elétricos.
- Cones: Detectam cores (vermelho, verde e azul).
- visão policromática (colorida), funcionam sob alta luminosidade, acuidade visual;
- Bastonetes: Detectam intensidades de luz (cinza), responsáveis pela visão periférica e noturna.
- mais numerosos, visão monocromática (noturna),funcionam sob baixa luminosidade;
- Cones: Detectam cores (vermelho, verde e azul).
Introdução
Características ópticas da luz
A luz é uma radiação eletromagnética que interage com as superfícies por:
reflexão - como a luz é refletida;
absorção - como a luz é absorvida;
transmissão - como a luz passa através de um objeto.
Espectro eletromagnético
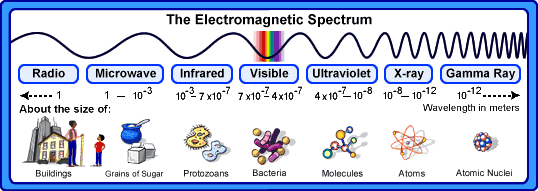
Introdução
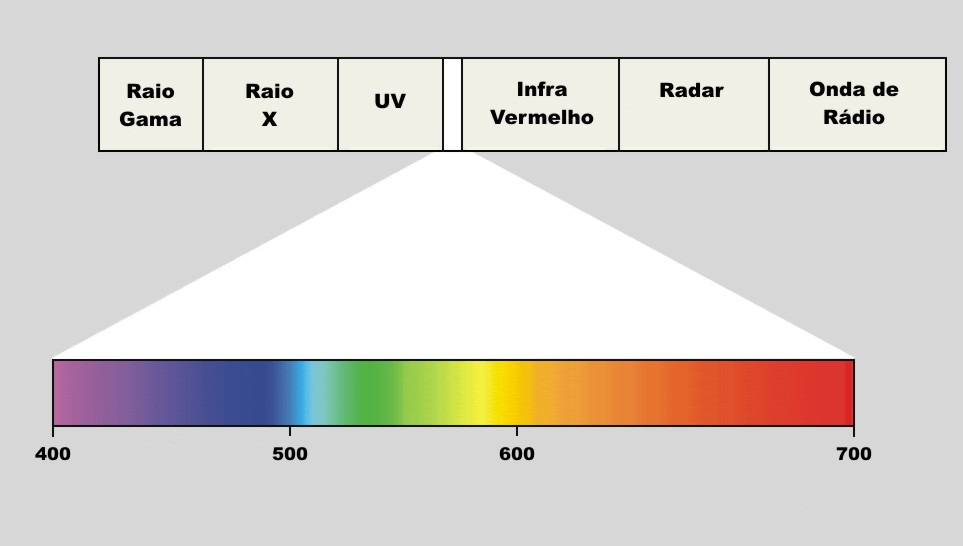
Espectro eletromagnético e comprimentos de onda da luz visível
- A luz visível é uma pequena parte do espectro eletromagnético, com comprimentos de onda entre 400 e 700 nm.
Introdução
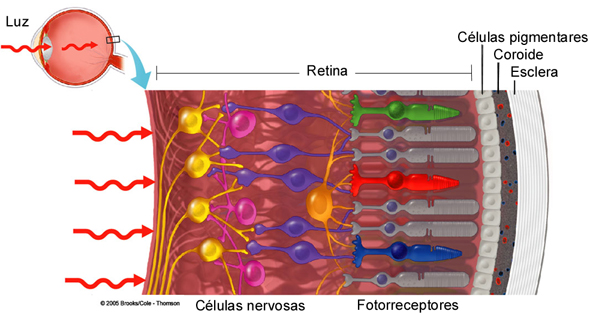
Retina. Fonte: https://www2.ibb.unesp.br/nadi/Museu2_qualidade/Museu2_corpo_humano/Museu2_como_funciona/Museu_homem_nervoso/Museu_homem_nervoso_visao/Museu2_homem_nervoso_visao_mecanismo.htm
Introdução
- Distribuição de cones na retina não é uniforme

Introdução
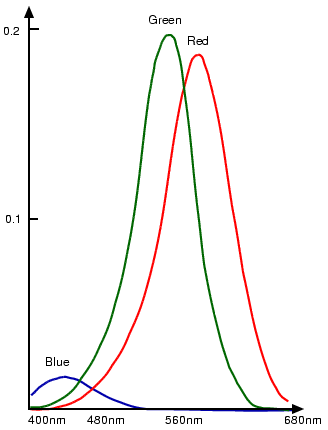
ABSORÇÃO DA LUZ PELOS PIGMENTOS VISUAIS.
Introdução
Proporção de Cones na Visão Humana
- Cones Vermelhos (L-Cones):
- Aproximadamente 64% dos cones.
- Sensíveis a comprimentos de onda longos (vermelho).
- Cones Verdes (M-Cones):
- Aproximadamente 32% dos cones.
- Sensíveis a comprimentos de onda médios (verde).
- Cones Azuis (S-Cones):
- Aproximadamente 2% dos cones.
- Sensíveis a comprimentos de onda curtos (azul).
Introdução
A visão humana é altamente adaptada para responder eficientemente às condições de luz natural e às necessidades evolutivas.
A proporção desigual de cones vermelhos, verdes e azuis permite um equilíbrio entre a acuidade visual, a percepção de cores e a minimização de distorções ópticas.
Como por exemplo, a luz azul:
A luz azul é menos prevalente na luz natural e ambiente em comparação com a luz vermelha e verde.
A menor quantidade de cones azuis ajuda a equilibrar a sensibilidade geral à luz.
Ter menos cones azuis ajuda a minimizar aberrações cromáticas, melhorando a nitidez da visão.
A refração mais forte da luz azul pode causar aberrações cromáticas, onde diferentes cores são focadas em diferentes pontos na retina, resultando em imagens borradas.
Introdução
Mas onde queremos chegar com tuddo isso?
Queremos quantificar as cores para conseguir reproduzir imagens em um ambiente digital!!!
Espaços de Cores
Para que a quantificação seja possível, é e necessário um domínio para se trabalhar com a cor, ou seja, um espaço de cores.
Este deve ter as seguintes propriedades: Capacidade de representar a maior quantidade de cores possíveis.
Possuir uma base (com o menor numero de cores possíveis) capaz de gerar todo o espaço.
Considerar ao máximo as características fisiológicas do sistema ótico e subjetivas do sistema perceptivo.
Introdução
Espaço RGB de Cores
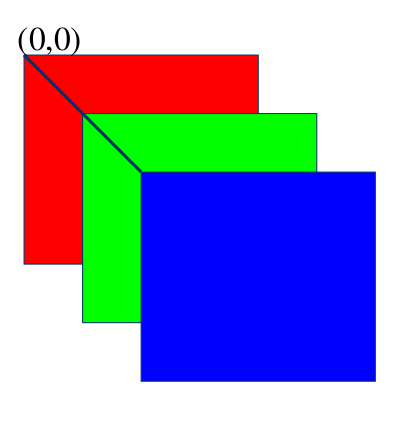
Um único pixel consiste de três componentes que variam entre [0,255].
Cada pixel e um vetor:
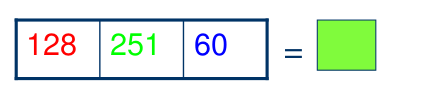
Vetor-pixel na memória do computador
Pixel na imagem
Introdução




Introdução
Representação como pontos de um espaço 3D de Cor
Cores criadas com o vetor cromático R,G,B
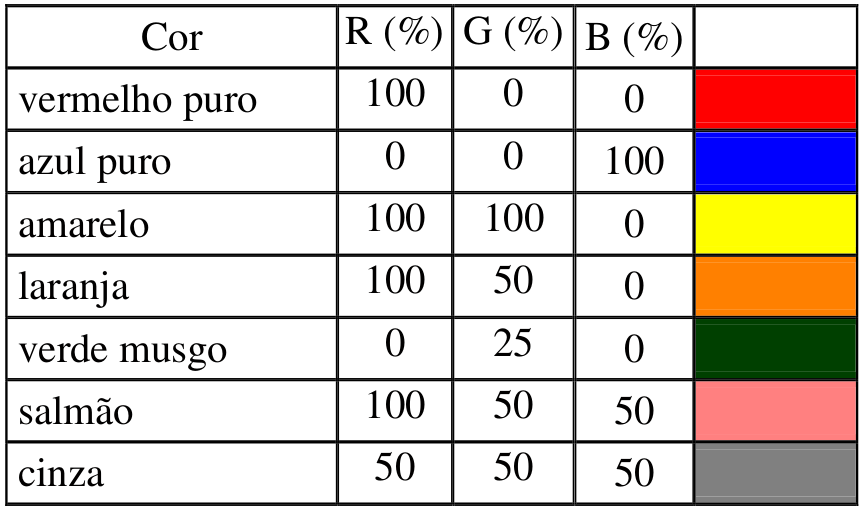
Introdução
\[ C=r\color{red}R+g\color{green}G+b\color{blue}B \]
onde \(\color{red}R\), \(\color{green}G\) e \(\color{blue}B\) são as cores primarias e \(r\), \(g\) e \(b\) os coeficientes da mistura.
Em geral define-se em três como o número de cores primarias em um espaço, devido ao fato do olho humano possuírem três tipos de fotorreceptores.
A partir destas cores primarias, é possível gerar todas as outras cores do espaço.
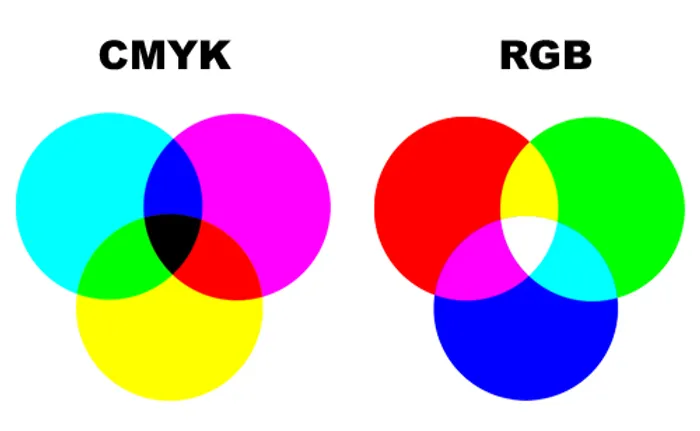
Entretanto, existem outras formas de representar cores, como o espaço CMYK.
O padrão RGB tem síntese aditiva, e é conhecido como cor luz, pois quando as três cores são sobrepostas formam o branco. Já o CMY tem síntese substrativa (também conhecido como pigmento), pois quando sobrepostas, as três cores formam a cor preto (K).
- Que são as cores que são utilizadas em impressoras.
Introdução
Entretanto, geralmente trabalha-se com a imagem em escala de cinza e normalizado, ou seja, com uma transformação da imagem colorida para uma imagem em tons de cinza.
Dessa forma, a imagem é representada por uma matriz de valores entre 0 e 1, onde 0 é o preto e 1 é o branco.
Converter cor RGB para tons de cinza

Introdução
Considere uma imagem colorida com três canais de cores (R, G, B) e um pixel \((R, G, B)\), onde \(R\), \(G\) e \(B\) são valores inteiros entre 0 e 255, com dimensão \(N \times M\), em que \(i\) e \(j\) são as coordenadas do pixel na imagem, sendo \(i \in [0, N-1]\) e \(j \in [0, M-1]\), em que \(n\) são as linhas e \(M\) as colunas da imagem e \(N \times M\) o número total de pixels na imagem.

Introdução
Fazemos a média dos valores de cada pixel para obter o valor do pixel na imagem em tons de cinza, e posterioemente normalizamos os valores para o intervalo \([0,1]\), dividindo pelo valor máximo que é \(255\).
Para cada pixel \((i,j)\), a intensidade média \(I^{(i,j)}_{\text{médio}}\) e a intensidade em tons de cinza \(I^{(i,j)}_{\text{cinza}}\) são dadas por:
\[ I^{(i,j)}_{\text{médio}} = \frac{R^{(i,j)}+G^{(i,j)}+B^{(i,j)}}{3}, \quad \text{onde} \quad I^{(i,j)}_{\text{médio}} \in [0,255], \]
\[ I^{(i,j)}_{\text{cinza}} = \frac{I^{(i,j)}_{\text{médio}}}{255}, \quad \text{onde} \quad I^{(i,j)}_{\text{cinza}} \in [0,1]. \]
Introdução
As vantagens de trabalhar com a imagem em tons de cinza são:
Redução da dimensionalidade da imagem.
Simplificação do processamento de imagens.
Redução do tempo de processamento.
Facilidade de visualização e interpretação.
Possibilita distinguir objetos, independente da luminosidade do ambiente.
Desacopla a informação de cor da informação de intensidade.
As Redes Neurais Convolucionais já foram desenvolvidas para trabalhar com as 3 camadas RGB
Redes Neurais Convolucionais
O que são Redes Neurais Convolucionais (CNNs)?
As CNNs são um tipo de rede neural artificial que é inspirada no córtex visual do cérebro humano.
são amplamente utilizadas para tarefas de visão computacional, como reconhecimento de imagens, detecção de objetos e segmentação de imagens.
els são capazes de aprender automaticamente características e padrões de imagens, sem a necessidade de extração manual de características.
As CNNs são compostas por camadas convolucionais, camadas de pooling e camadas totalmente conectadas.
Redes Neurais Convolucionais
O que são Redes Neurais Convolucionais (CNNs)?
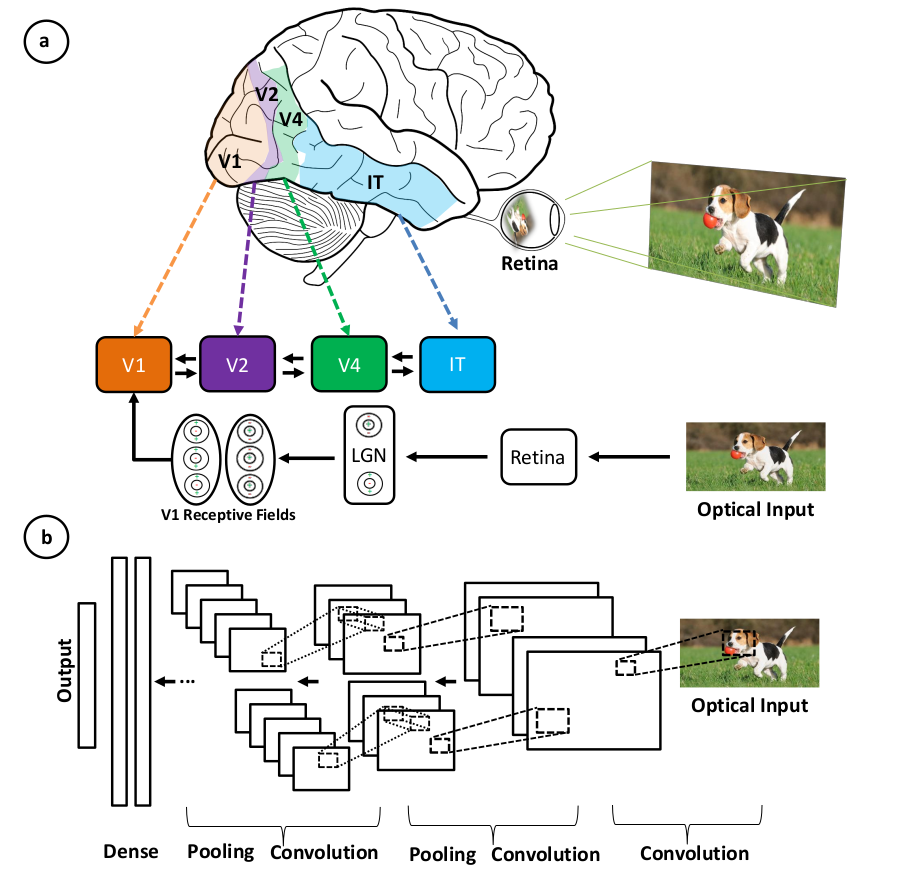
- Camadas Convolucionais: Similar à forma como o córtex visual processa informações visuais em camadas.
- Extração de Características: CNNs extraem características (bordas, texturas) como o cérebro detecta formas e padrões.
- Pooling: Redução da dimensionalidade e abstração de informações, semelhante ao processamento hierárquico do cérebro.
Redes Neurais Convolucionais
Uma Rede Neural Convolucional (CNN) não representa uma ideia nova.
Este modelo já havia se mostrado eficaz para o reconhecimento de dígitos manuscritos em 1998 (Yann, 1998).
No entanto, devido à incapacidade dessas redes de escalarem para imagens maiores, elas lentamente perderam o interesse da comunidade.
A principal razão estava relacionada às limitações de memória, hardware e à indisponibilidade de quantidades suficientemente grandes de dados de treinamento.
Com o aumento do poder computacional, graças à ampla disponibilidade de GPUs, e à introdução de conjuntos de dados em larga escala, foi possível treinar modelos maiores e mais complexos.
Isso estimulou amplamente o uso de redes profundas na área de imagens.
Redes Neurais Convolucionais
Um pouco de história
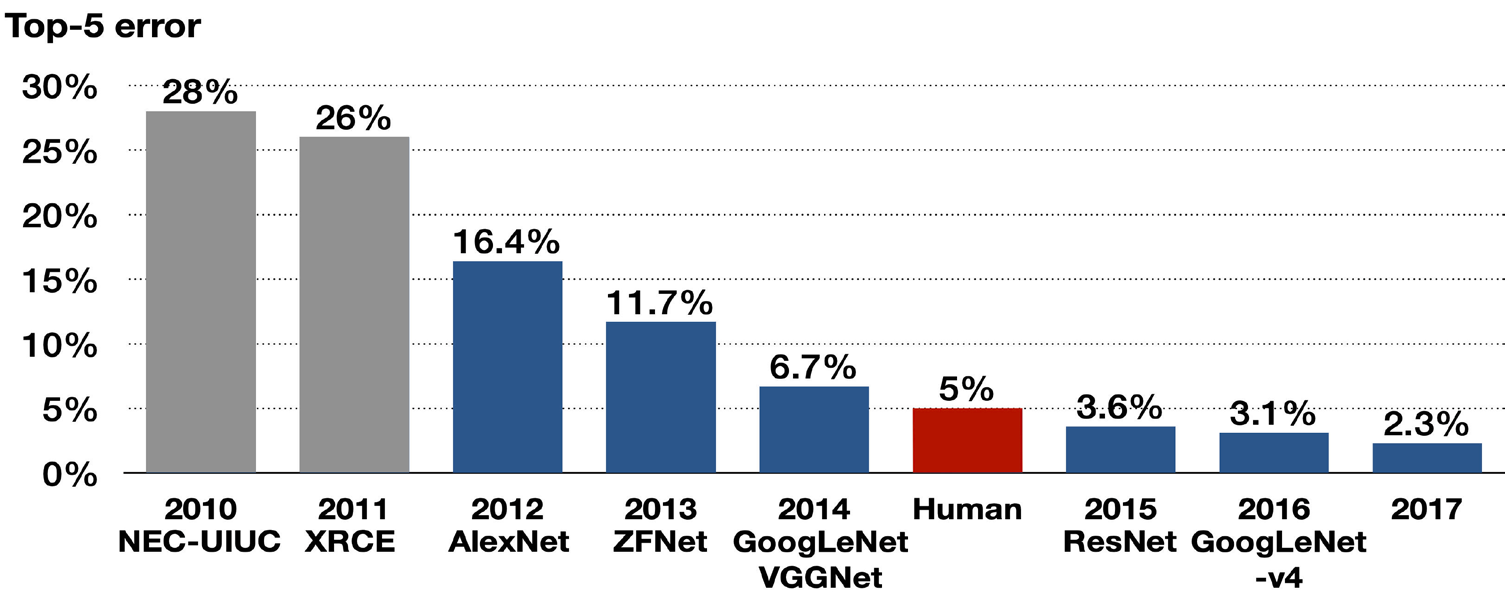
O ImageNet Large-Scale Visual Recognition Challenge (ILSVRC) era uma competição anual de reconhecimento visual em larga escala, que começou em 2010-2017. A competição era baseada no banco de dados ImageNet, que contém milhões de imagens anotadas em milhares de categorias.
Em 2012, a equipe da Universidade de Toronto, liderada por Alex Krizhevsky, Ilya Sutskever e Geoffrey Hinton, desenvolveu uma CNN chamada AlexNet (paper), que obteve uma precisão de erro de 16,4%, superando significativamente os métodos tradicionais e significativamente melhor que o segundo colocado do mesmo ano, que teve uma taxa de erro de 26,2%.
Redes Neurais Convolucionais
Redes Neurais Convolucionais
As Redes Neurais Convolucionais (CNNs) continuaram atraindo a atenção após vencerem o Desafio ImageNet até o ano de 2017.
Existiam 50.000 imagens coloridas de alta resolução em 1.000 categorias;
O treinamento com 1,2 milhão de imagens;
Em 2017, a SENet (https://arxiv.org/abs/1709.01507) alcançou uma taxa de erro de 2,3% em 2017.
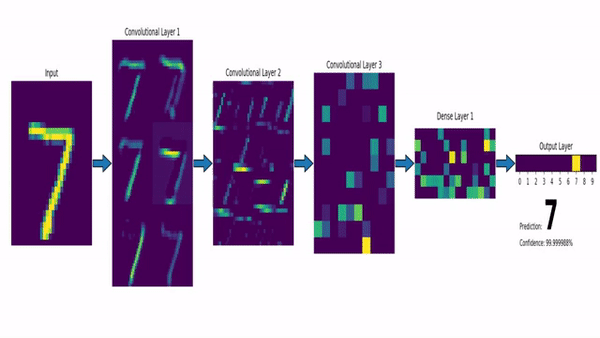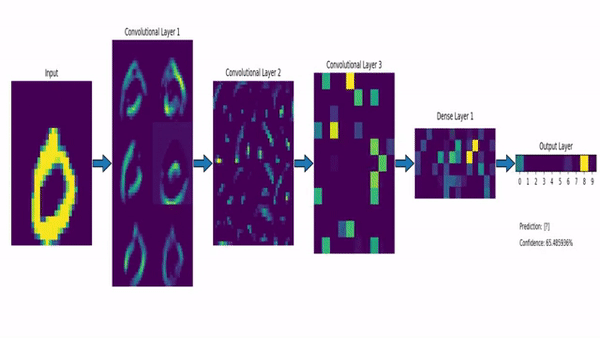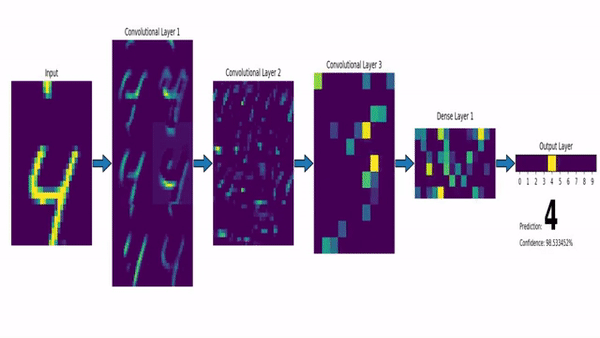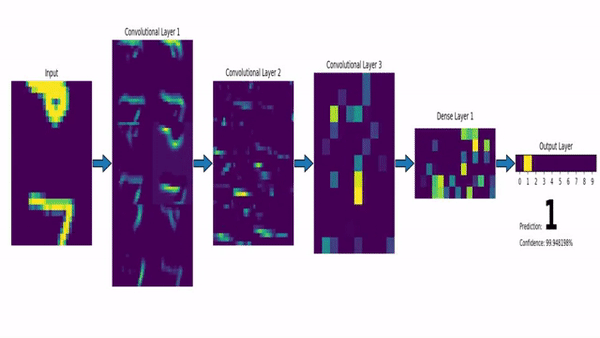
Redes Neurais Convolucionais
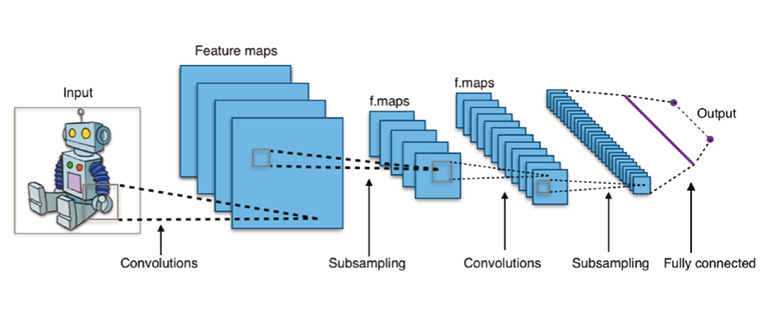
- A Figura acima mostra uma arquitetura típica de uma rede neural convolucional que contém uma camada de entrada, camadas convolucionais, camadas de pooling (subamostragem, ou down sampling), camadas de ativação, camadas totalmente conectadas e uma camada de saída.
Redes Neurais Convolucionais
Componentes de uma CNN
- Camada de Entrada:
- Recebe os dados brutos, geralmente uma imagem, que será processada pelas camadas subsequentes.
- Camadas Convolucionais:
- Responsáveis pela aplicação de filtros à imagem de entrada para extrair características importantes, como bordas, texturas e padrões. Esses filtros são ajustados durante o treinamento da rede.
- Camadas de Pooling:
- Também conhecidas como camadas de subamostragem ou down sampling, reduzem a dimensionalidade dos dados, preservando as características importantes. Isso ajuda a reduzir a complexidade computacional e a evitar o overfitting.
Redes Neurais Convolucionais
- Camadas de Ativação:
- Aplicam funções de ativação, como ReLU (Rectified Linear Unit), para introduzir não-linearidades no modelo, permitindo que a rede aprenda relações complexas entre os dados.
- Camadas Totalmente Conectadas:
- Conectam todas as unidades da camada anterior a todas as unidades da próxima camada, integrando as características extraídas pelas camadas convolucionais e realizando a classificação ou predição final.
- Camada de Saída:
- Produz a predição final da rede, que pode ser uma classificação de imagem, detecção de objeto ou outra tarefa específica.
Redes Neurais Convolucionais
Camadas Convolucionais
As camadas convolucionais são responsáveis por aplicar filtros à imagem de entrada para extrair características importantes, como bordas, texturas e padrões.
Cada filtro é uma matriz de pesos que é aplicada à imagem de entrada por meio de uma operação de convolução.
A operação de convolução é uma operação matemática que combina duas funções para produzir uma terceira função.
A operação de convolução é realizada deslizando o filtro sobre a imagem de entrada e multiplicando os valores do filtro pelos valores correspondentes da imagem de entrada.
A saída da operação de convolução é chamada de mapa de características ou feature map.
Redes Neurais Convolucionais
Temos que a convolução é dada por:
\[ (f * g)(t) \equiv \int_{-\infty}^{\infty} f(\tau)g(t-\tau)d\tau = \int_{-\infty}^{\infty} g(\tau)f(t-\tau)d\tau \]
onde \(f\) e \(g\) são funções contínuas e \(*\) é o operador de convolução, em que geralmente escrevemos \(f * g\) como \(f \otimes g\).
Para sinais discretos, a convolução é dada por:
\[ (f * g)(n) \equiv \sum_{m=-\infty}^{\infty} f(m)g(n-m) = \sum_{m=-\infty}^{\infty} g(m)f(n-m) \]
onde \(f\) e \(g\) são sinais discretos e \(*\) é o operador de convolução.
Redes Neurais Convolucionais
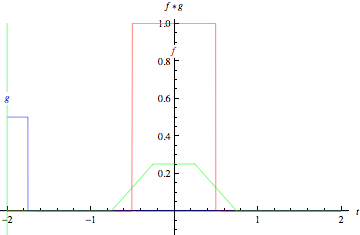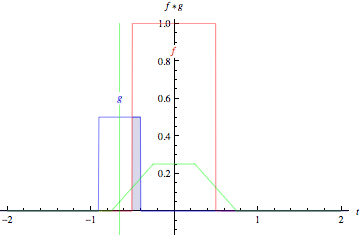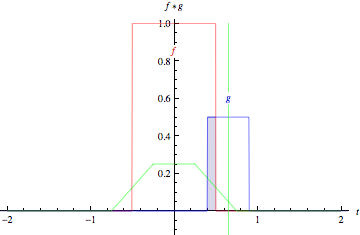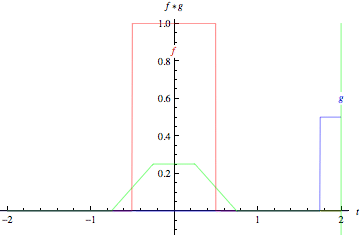
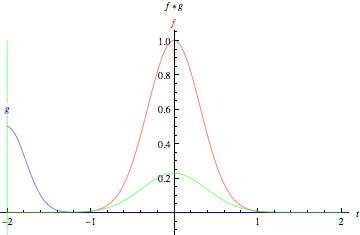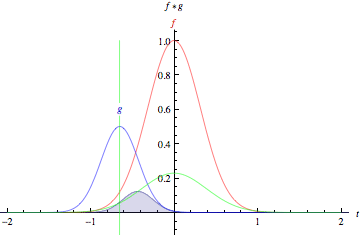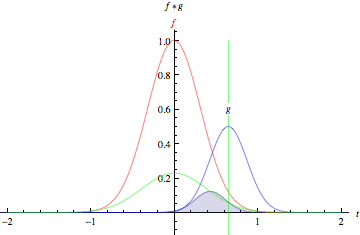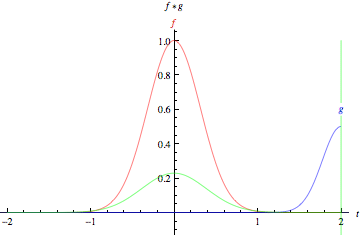
As animações acima ilustram graficamente a convolução de duas funções boxcar (à esquerda) e de duas funções Gaussianas (à direita).
Nos gráficos, a curva verde mostra a convolução das curvas azul e vermelha como uma função de \(t\), na posição indicada pela linha verde vertical.
A região cinza indica o produto \(g(\tau)f(t - \tau)\) como uma função de \(t\), então sua área como uma função de \(t\) é precisamente a convolução.
fonte: https://mathworld.wolfram.com/Convolution.html
Redes Neurais Convolucionais
Nesse caso das imagens, é utilizado a convolução discreta 2D (também conhecida como correlação cruzada 2D), onde a operação de convolução é realizada deslizando um filtro sobre a imagem de entrada e multiplicando os valores do filtro pelos valores correspondentes da imagem.
A convolução 2D, é definida como:
\[
S(i,j) = (f * g)(i,j) = \sum_{k=0}^{N-1} \sum_{l=0}^{M-1} g(k,l)f(i+k,j+l),
\]
em que \(f\) é a imagem de entrada, \(g\) é um filtro, \(S\) é a matriz resultante da convolução, \(*\) é o operador de convolução. Nesse caso, \(S\) e \(f\) são matrizes com \(N\) linhas e \(M\) colunas, e \(g\) é um filtro com \(n\) linhas e \(m\) colunas.
Redes Neurais Convolucionais
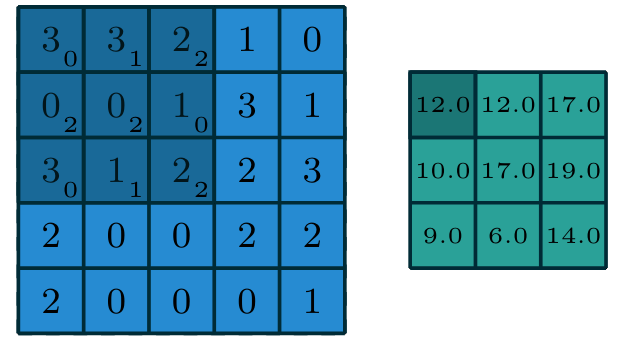
Exemplo 1 de convolução
- Imagem: \(im\) de dimensões \((5 \times 5)\)
- Filtro ou kernel: \(g\) de dimensões \((3 \times 3)\)
Redes Neurais Convolucionais
Exemplo 1 de convolução - cont.
\(S(0,0) = (0 \cdot 3) + (1\cdot3) + (2\cdot2) + (2\cdot0) + (2\cdot0) + (0\cdot1) + (0\cdot3) + (1\cdot1) + (2\cdot2) = 12\)
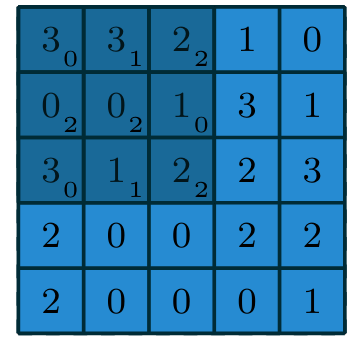
Encontrem para:
\(S(0,1) = ?\)
\(S(1,0) = ?\)
\(S(1,1) = ?\)
Redes Neurais Convolucionais
Exemplo 1 de convolução - cont.
\(S(0,0) = (0 \cdot 3) + (1\cdot3) + (2\cdot2) + (2\cdot0) + (2\cdot0) + (0\cdot1) + (0\cdot3) + (1\cdot1) + (2\cdot2) = 12\)

Encontrem para:
\(S(0,1) = 12\)
\(S(1,0) = 10\)
\(S(1,1) = 17\)
Redes Neurais Convolucionais
Dois conceitos importantes na camada de convolução são:
Stride: é o número de pixels que o filtro se move a cada passo. Um stride de 1 significa que o filtro se move um pixel por vez. Um stride de 2 significa que o filtro se move dois pixels por vez.
Padding: é a adição de pixels ao redor da imagem de entrada. O padding pode ser “valid” (sem padding) ou “same” (com padding). O padding “same” adiciona pixels à imagem de entrada para que a saída tenha o mesmo tamanho da entrada.
Vamos entender cada um deles e como isso afeta a matriz resultante da convolução, que em nosso caso estamos chamando de matriz \(S(i,j)\).
Vamos considerara que a imagem tem dimensões \(N \times M\) e o filtro \(g\) tem dimensões \(n \times m\), o Stride será denotado por \(s\) e o padding por \(p\).
Redes Neurais Convolucionais
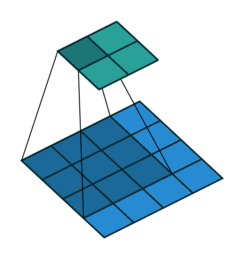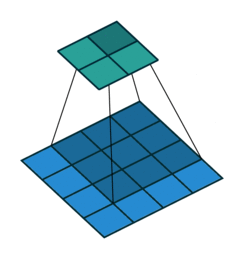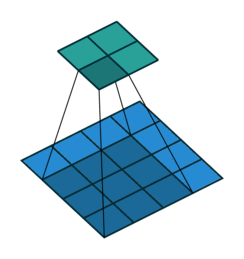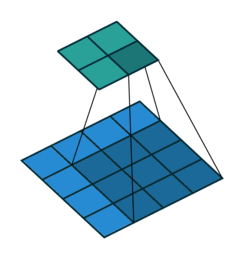
Relação 1: Zero padding, strides unitários
Neste caso, temos que a matriz resultante da convolução \(S\) irá possuir dimensões:
\[\begin{align} \begin{aligned} Nn = & (N - n) + 2p + s \\ Mm = & (M - m) + 2p + s \end{aligned} \end{align}\]
em que \(Nn\) e \(Mm\) são as dimensões da matriz resultante da convolução, \(N\) e \(M\) são as dimensões da imagem de entrada, \(n\) e \(m\) são as dimensões do filtro, \(p\) é o padding e \(s\) é o stride.
Logo, a matriz resultante da convolução \(S\) terá dimensões \((Nn \times Mm)\).
Redes Neurais Convolucionais
Relação 2: Half (same) padding, strides unitários
Neste caso, temos que a dimensão do filtro é determinada por:
\[\begin{align} \begin{aligned} n = & 2t +1, \forall t \in \mathbb{N} \\ m = & 2h +1, \forall h \in \mathbb{N} \end{aligned} \end{align}\]
com \(p_i = \lfloor i/2 \rfloor\)1, em que \(i \in \{n, m\}\). Assim, temos: \[\begin{align} \begin{aligned} Nn = & (N - n) + 2p_n + s = \left(N - (2t+1)\right) + 2\left\lfloor t + \frac{1}{2}\right\rfloor + 1 = N \\ Mm = & (M - m) + 2p_m + s = \left(M - (2h+1)\right) + 2\left\lfloor h + \frac{1}{2}\right\rfloor + 1 = M \end{aligned} \end{align}\]
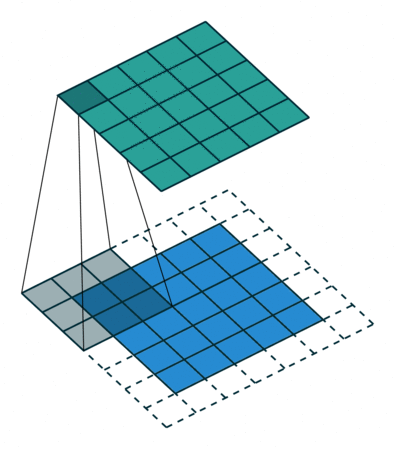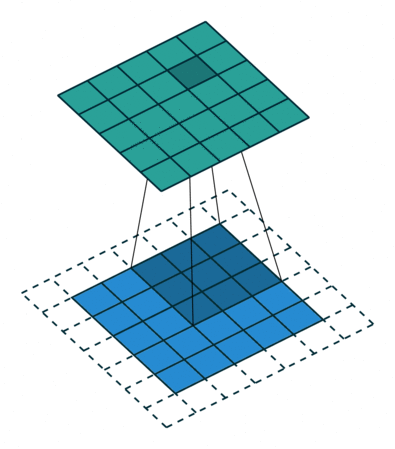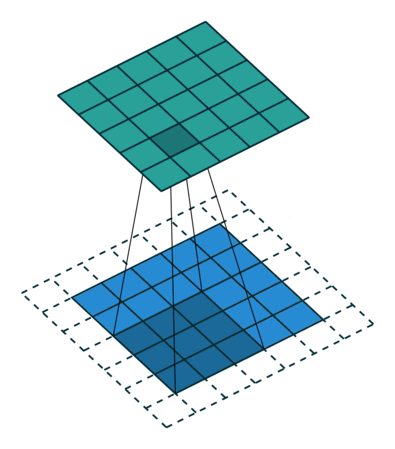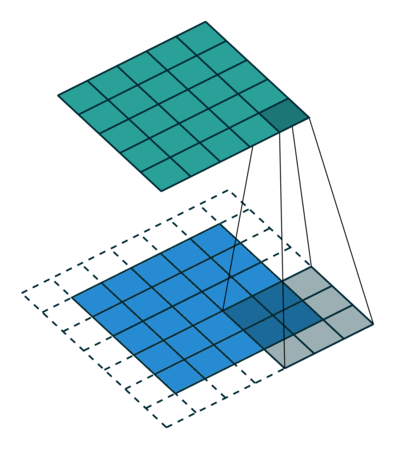
Logo, a matriz resultante da convolução \(S\) terá dimensões iguais a imagem de entrada, ou seja, \((N \times M)\).
Redes Neurais Convolucionais
Relação 3: Full padding, strides unitários
Neste caso, para uma determinada dimensão do filtro \(n\) e \(m\), temos que a dimensão da matriz resultante da convolução \(S\) é dada por:
\[\begin{align} \begin{aligned} Nn = & (N - n) + 2p_n + s \\ = & \left(N - n\right) + 2(n-1) + 1 = N + n - 1 \\ Mm = & (M - m) + 2p + s \\ = & \left(M - m\right) + 2(m - 1) + 1 = M + m - 1 \end{aligned} \end{align}\]
em que \(p_i = 2(i-1)\), em que \(i \in \{n, m\}\). Assim, temos que a matriz resultante da convolução \(S\) terá dimensões \((N + n - 1) \times (M + m - 1)\).
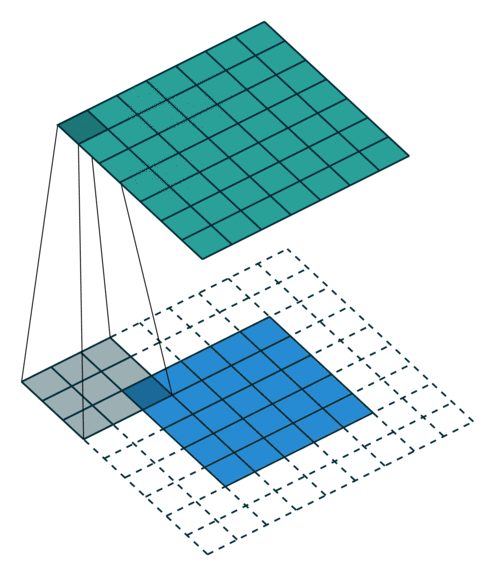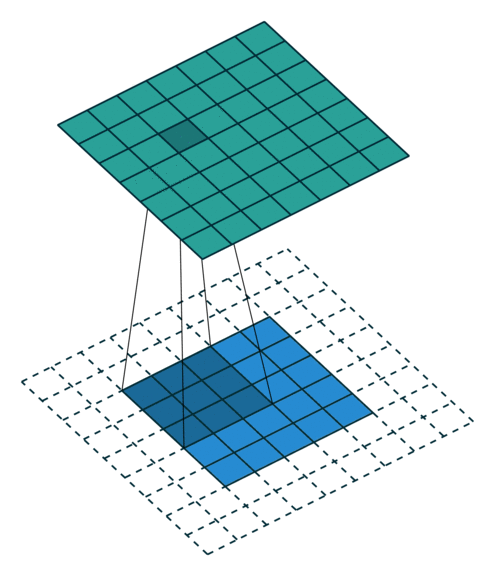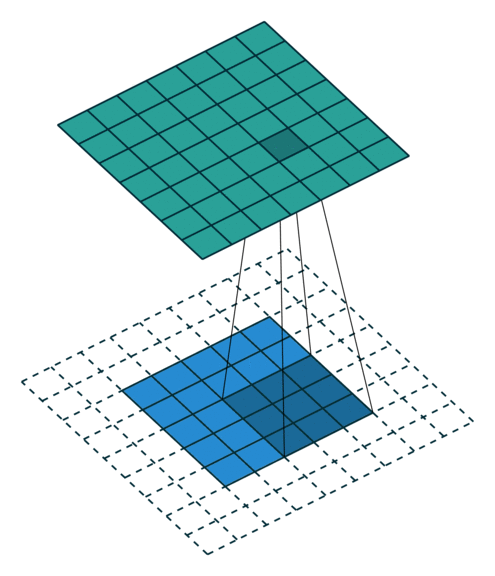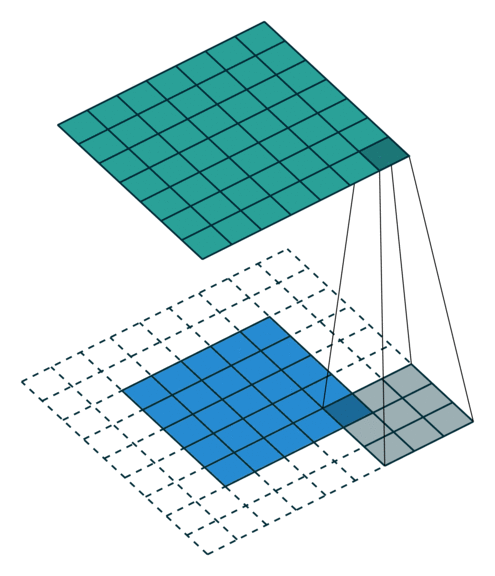
Redes Neurais Convolucionais
Relação 4: padding zerado, strides não unitários
Neste caso, para uma determinada dimensão do filtro \(n\) e \(m\), com \(s \geq 1\), e \(p = 0\), temos que a dimensão da matriz resultante da convolução \(S\) é dada por:
\[\begin{align} \begin{aligned} Nn = & \left\lfloor \dfrac{N - n + 2p}{s}\right\rfloor + 1 = \left\lfloor \dfrac{N - n}{s}\right\rfloor + 1 \\ Mm = & \left\lfloor \dfrac{M - m + 2p}{s}\right\rfloor + 1 = \left\lfloor \dfrac{M - m }{s}\right\rfloor + 1 \end{aligned} \end{align}\]
em que \(\lfloor \cdot \rfloor\) indica a função piso que retorna a parte inteira de \(\cdot\), descartando qualquer parte fracionária.
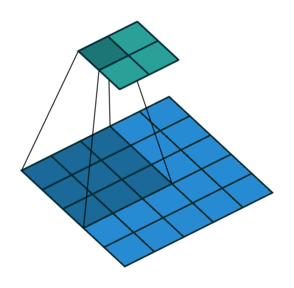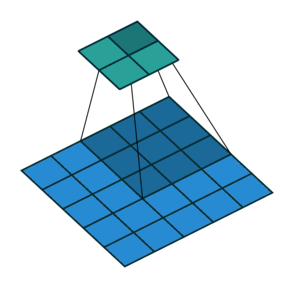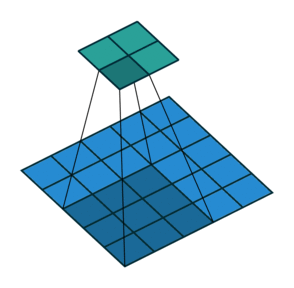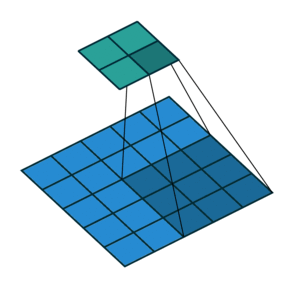
Assim, temos que \(Nn \times Mm\) representam as dimensões da matriz resultante da convolução \(S\).
Redes Neurais Convolucionais
Relação 5: padding não zerados, strides não unitários
Neste caso, para uma determinada dimensão do filtro \(n\) e \(m\), com \(s \geq 1\), e \(p > 0\) temos que a dimensão da matriz resultante da convolução \(S\) é dada por:
\[\begin{align} \begin{aligned} Nn = & \left\lfloor \dfrac{N - n + 2p}{s}\right\rfloor + 1 \\ Mm = & \left\lfloor \dfrac{M - m + 2p}{s}\right\rfloor + 1 \end{aligned} \end{align}\]
em que \(\lfloor \cdot \rfloor\) indica a função piso que retorna a parte inteira de \(\cdot\), descartando qualquer parte fracionária.
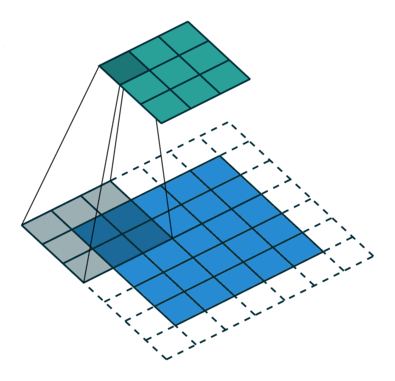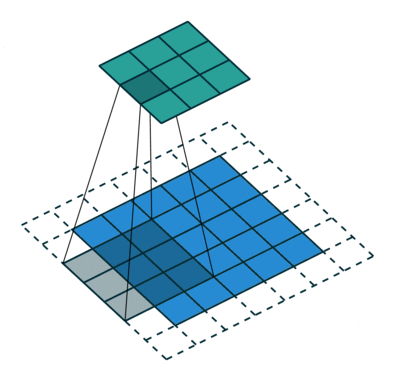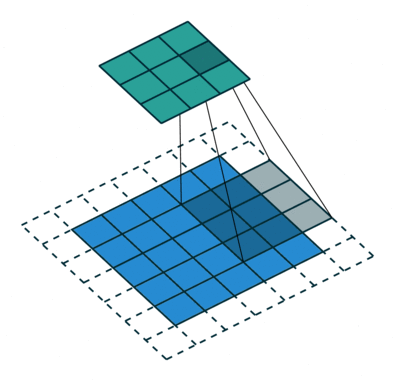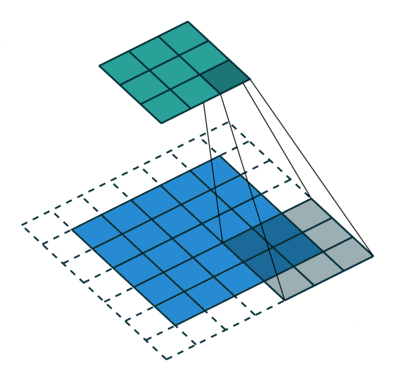
Assim, temos que \(Nn \times Mm\) representam as dimensões da matriz resultante da convolução \(S\).
Redes Neurais Convolucionais
Filtros e Mapas de Características
Os filtros são matrizes de pesos que são aplicadas à imagem de entrada para extrair características importantes, como bordas, texturas e padrões.
Vamos passar por alguns como os filtros Prewitt, Sobel, Laplaciano;
Vamos utilizar a seguinte imagem abaixo:

Redes Neurais Convolucionais
Filtros e Mapas de Características
Filtro Identidade:
O filtro identidade em Redes Neurais Convolucionais (CNN) é um kernel que, quando aplicado a uma imagem, retorna a própria imagem sem alterações, permitindo que todos os valores de pixel passem inalterados através da operação de convolução.
\[\begin{align} g = \begin{bmatrix} 0 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \\ \end{bmatrix} \end{align}\]

Redes Neurais Convolucionais
Filtros e Mapas de Características
Filtro da Média ou Passa Baixa:
O filtro passa-baixa, também conhecido como filtro de média, é utilizado em Redes Neurais Convolucionais para suavizar a imagem, reduzindo o ruído e as variações rápidas de intensidade, permitindo apenas a passagem das componentes de baixa frequência.
\[\begin{align} g = \begin{bmatrix} 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \\ \end{bmatrix} \end{align}\]

Redes Neurais Convolucionais
Filtros e Mapas de Características
Filtro de Sharpen ou Passa Alta:
O filtro passa-alta, também conhecido como filtro de “sharpen” (nitidez), é utilizado em Redes Neurais Convolucionais para realçar os detalhes e as bordas de uma imagem, aumentando o contraste entre os pixels vizinhos e tornando a imagem mais nítida.
\[\begin{align} g = \begin{bmatrix} 0 & -1 & 0 \\ -1 & 5 & -1 \\ 0 & -1 & 0 \\ \end{bmatrix} \end{align}\]

Redes Neurais Convolucionais
Filtros e Mapas de Características
Filtro de Prewitt:
O operador de Prewitt é composto por dois filtros que ajudam a detectar bordas verticais e horizontais. O filtro horizontal (direção x) ajuda a detectar bordas na imagem que cortam perpendicularmente o eixo horizontal, e vice-versa para o filtro vertical (direção y).
\[\begin{align} \text{Horizontal: }g = \begin{bmatrix} -1 & 0 & 1 \\ -1 & 0 & 1 \\ -1 & 0 & 1 \\ \end{bmatrix} \end{align}\]
\[\begin{align} \text{Vertical: }g = \begin{bmatrix} -1 & -1 & -1 \\ 0 & 0 & 0 \\ 1 & 1 & 1 \\ \end{bmatrix} \end{align}\]


Redes Neurais Convolucionais
Filtros e Mapas de Características
Filtro Laplaciano:
Ao contrário dos filtros Prewitt e Sobel, o filtro Laplaciano é um único filtro que detecta bordas em diferentes orientações. Do ponto de vista matemático, ele calcula derivadas de segunda ordem.
\[\begin{align} g = \begin{bmatrix} -1 & -1 & -1 \\ -1 & 8 & -1 \\ -1 & -1 & -1 \\ \end{bmatrix} \end{align}\]

Redes Neurais Convolucionais
Filtros e Mapas de Características
Filtros Robinson Compass:
As máscaras Robinson Compass são filtros de detecção de bordas compostos por 8 filtros diferentes, correspondentes às 8 direções geográficas da bússola. Esses filtros ajudam a detectar bordas orientadas nessas direções da bússola.
Oeste
\[\begin{align} \begin{bmatrix} -1 & 0 & 1 \\ -2 & 0 & 2 \\ -1 & 0 & 1 \\ \end{bmatrix} \end{align}\]
Sudoeste
\[\begin{align} \begin{bmatrix} 0 & 1 & 2 \\ -1 & 0 & 1 \\ -2 & -1 & 0 \\ \end{bmatrix} \end{align}\]
Sul
\[\begin{align} \begin{bmatrix} 1 & 2 & 1 \\ 0 & 0 & 0 \\ -1 & -2 & -1 \\ \end{bmatrix} \end{align}\]
Sudeste
\[\begin{align} \begin{bmatrix} 2 & 1 & 0 \\ 1 & 0 & -1 \\ 0 & -1 & -2 \\ \end{bmatrix} \end{align}\]
Leste
\[\begin{align} \begin{bmatrix} 1 & 0 & -1 \\ 2 & 0 & -2 \\ 1 & 0 & -1 \\ \end{bmatrix} \end{align}\]
Nordeste
\[\begin{align} \begin{bmatrix} 0 & -1 & -2 \\ 1 & 0 & -1 \\ 2 & 1 & 0 \\ \end{bmatrix} \end{align}\]
Norte
\[\begin{align} \begin{bmatrix} -1 & -2 & -1 \\ 0 & 0 & 0 \\ 1 & 2 & 1 \\ \end{bmatrix} \end{align}\]
Noroeste
\[\begin{align} \begin{bmatrix} -2 & -1 & 0 \\ -1 & 0 & 1 \\ 0 & 1 & 2 \\ \end{bmatrix} \end{align}\]
Redes Neurais Convolucionais
As convoluções geralmente são calculadas para cada canal e somadas:
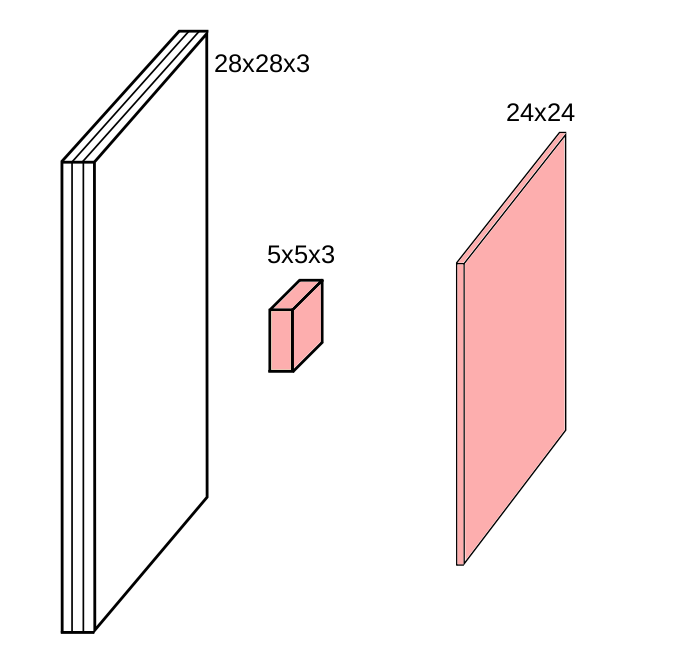
Redes Neurais Convolucionais
As convoluções geralmente são calculadas para cada canal e somadas:
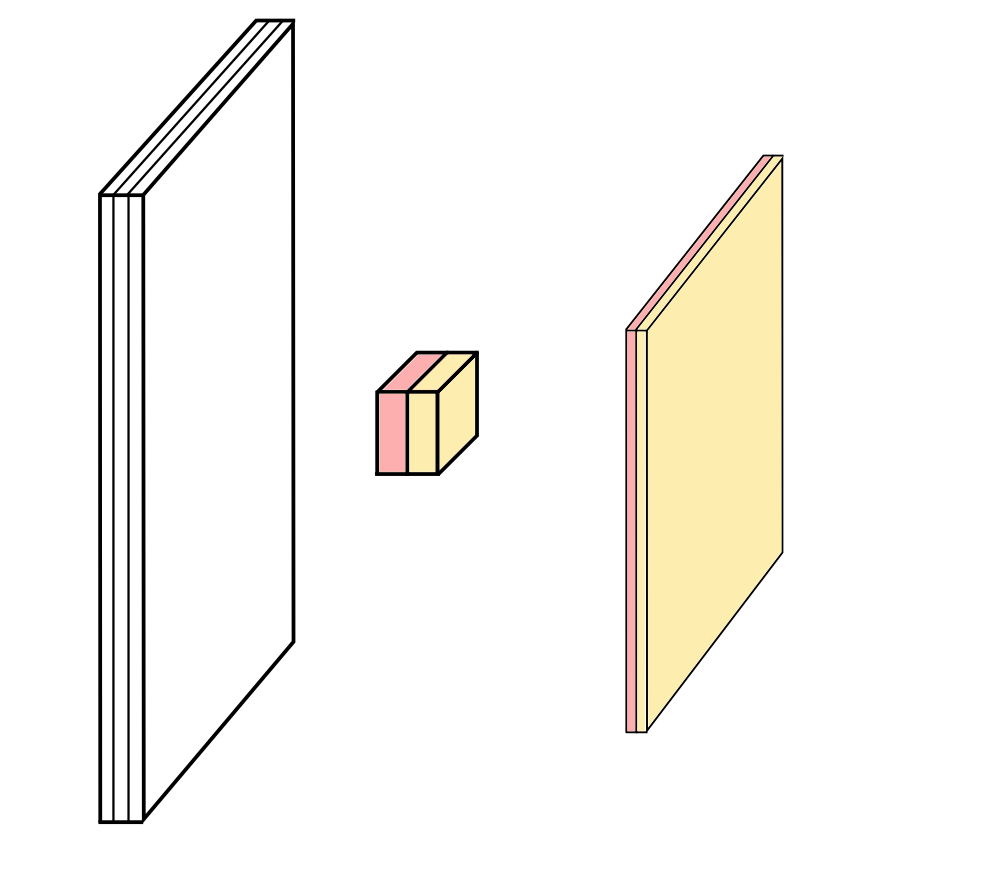
Redes Neurais Convolucionais
As convoluções geralmente são calculadas para cada canal e somadas:
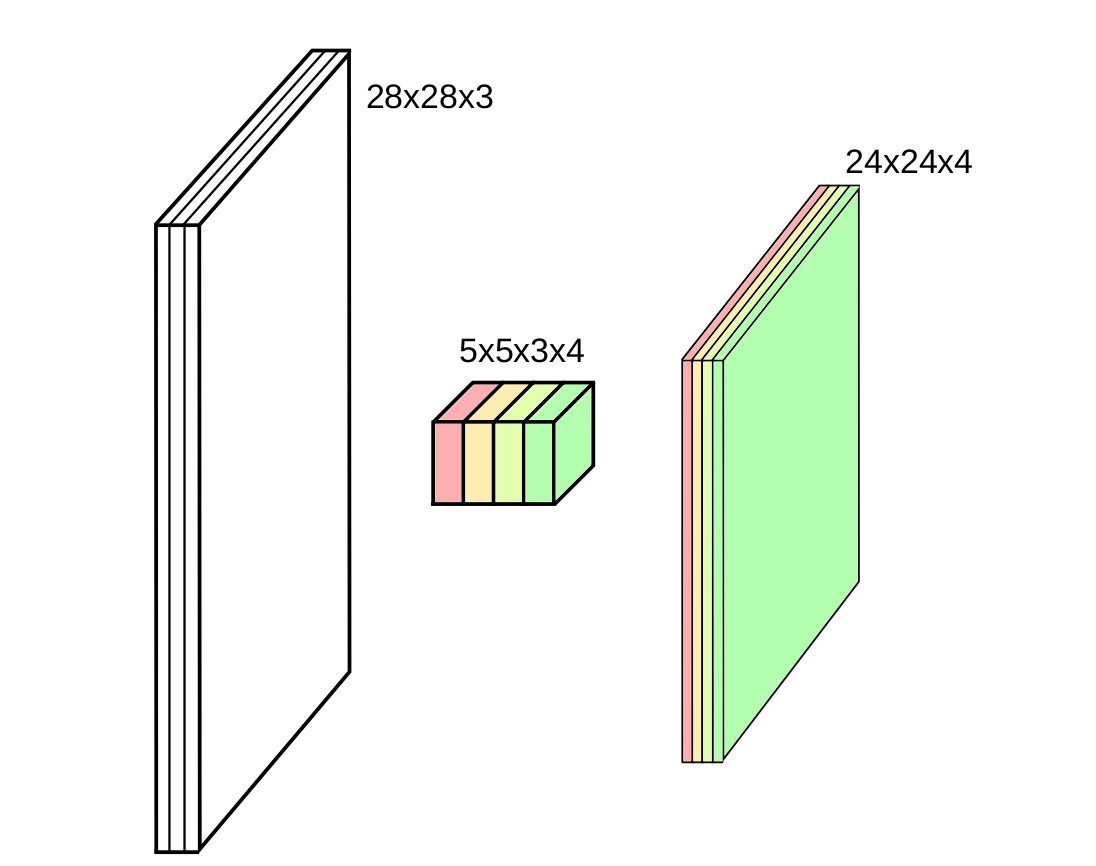
Redes Neurais Convolucionais
Em geral trabalha-se com tamanhos de dimensões de kernel: 1, 3, 5, 7, 11;
A dimensão do kernel é um número ímpar, pois isso garante que o kernel tenha um centro.
O número de filtros é um hiperparâmetro que deve ser ajustado.
O número de filtros determina a profundidade da camada convolucional.
Cada filtro aprende a detectar um padrão específico na imagem.
Quanto mais filtros, mais padrões diferentes a camada convolucional pode aprender.
Redes Neurais Convolucionais
Camada Pooling
A camada de pooling é usada para reduzir a dimensionalidade dos mapas de características, mantendo as características mais importantes.
O pooling é feito deslizando um filtro sobre o mapa de características e aplicando uma operação, como a média ou o máximo, para reduzir a dimensionalidade.
O pooling ajuda a reduzir o overfitting e o tempo de computação.
O pooling também ajuda a tornar a rede invariante a pequenas translações e distorções na imagem.
As camadas pooling ficam entre camadas convolucionais em uma arquitetura de CNN.
Redes Neurais Convolucionais
Camada Pooling
Sua função é reduzir progressivamente o tamanho espacial da representação para reduzir a quantidade de parâmetros e o cálculo na rede, e, portanto, também controlar o overfitting.
A Camada de Pooling opera independentemente em cada fatia de profundidade da entrada e redimensiona-a espacialmente, utilizando a operação de MÁXIMO.
A forma mais comum é uma camada de pooling com filtros de tamanho \(2 \times 2\) aplicados com um stride de 2, que reduz cada fatia de profundidade na entrada por 2 ao longo tanto da largura quanto da altura, descartando 75% das ativações.
Cada operação de MÁXIMO, nesse caso, estaria considerando o máximo entre 4 números (pequena região \(2 \times 2\) em alguma fatia de profundidade).
Redes Neurais Convolucionais
- A dimensão de profundidade permanece inalterada. De forma mais geral, a camada de pooling:
- Aceita um volume de tamanho \(W_1 \times H_1 \times D_1\);
- Requer dois hiperparâmetros:
- sua extensão espacial \(F\),
- o stride \(S\),
- Produz um volume de tamanho \(W_2 \times H_2 \times D_2\) onde:
- \(W_2 = (W_1 - F)/S + 1\),
- \(H_2 = (H_1 - F)/S + 1\),
- \(D_2 = D_1\).
- Introduz zero parâmetros, pois calcula uma função fixa da entrada.
- Para camadas de Pooling, não é comum preencher a entrada usando zero-padding.
Redes Neurais Convolucionais
- Vale notar que existem apenas duas variações comumente vistas da camada de max pooling na prática:
- uma camada de pooling com \(F = 3, S = 2\) (também chamada de overlapping pooling),
- e mais comumente \(F = 2, S = 2\).
- Tamanhos de pooling com campos receptivos maiores são muito destrutivos.
Pooling geral. Além do max pooling, as unidades de pooling também podem realizar outras funções, como average pooling ou até mesmo L2-norm pooling. O average pooling era frequentemente usado historicamente, mas recentemente caiu em desuso em comparação com a operação de max pooling, que demonstrou funcionar melhor na prática.
Redes Neurais Convolucionais
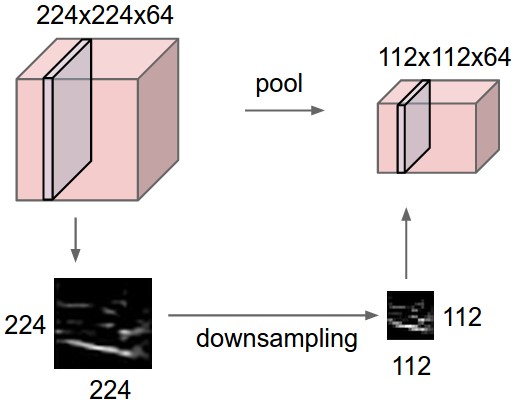
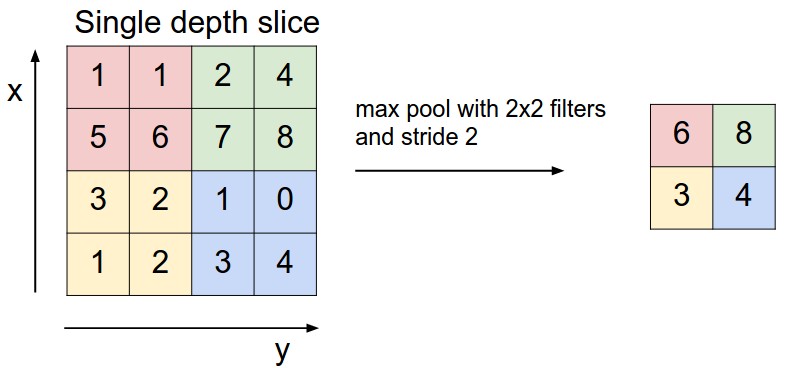
À esquerda: Neste exemplo, o volume de entrada de tamanho \([224 \times 224 \times 64]\) é reduzido com um filtro de tamanho 2 e stride 2 para um volume de saída de tamanho \([112 \times 112 \times 64]\). Observe que a profundidade do volume é preservada. À direita: A operação de downsampling mais comum é a de máximo, dando origem ao max pooling, aqui mostrado com um stride de 2. Ou seja, cada máximo é calculado sobre 4 números (pequeno quadrado \(2 \times 2\)).
Redes Neurais Convolucionais
Na primeira linha, imagem de referência através de 3 iterações progressivas de max pooling usando um kernel de (2, 2). Na segunda linha, a imagem de referência através de 3 iterações progressivas de average pooling usando um kernel de (3, 3).


Redes Neurais Convolucionais
- Até o momento, várias CNNs foram desenvolvidas, como LeNet, AlexNet, GoogLeNet (agora Inception), VGG, ResNet, DenseNet, MobileNet, EfficientNet, YOLO, entre outras.
Vamos entender a arquitetura da AlexNet
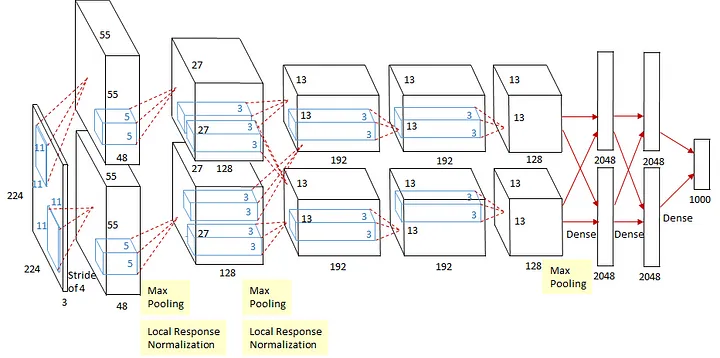
Redes Neurais Convolucionais
Vamos entender a arquitetura da AlexNet

AlexNet contém oito camadas:
Entrada: Imagens de entrada de \(224 \times 224 \times 3\)
1ª Camada convolucional: 2 grupos de 48 kernels, tamanhos \(11 \times 11 \times 3\) (stride: 4, pad: 0)
Redes Neurais Convolucionais
Vamos entender a arquitetura da AlexNet

- Saídas: \(55 \times 55 \times 48\) mapas de características em \(\times 2\) grupos. Então, Max Pooling sobreposto \(3 \times 3\) (stride: 2)
- Saídas: \(27 \times 27 \times 48\) mapas de características \(\times 2\) grupos. Então, Normalização de Resposta Local
- Saídas: \(27 \times 27 \times 48\) mapas de características \(\times 2\) grupos.
Redes Neurais Convolucionais
Vamos entender a arquitetura da AlexNet

- 2ª: Camada Convolucional: 2 grupos de 128 kernels de tamanho \(5 \times 5 \times 48\) (stride: 1, pad: 2)
- Saídas: \(27 \times 27 \times 128\) mapas de características em \(\times 2\) grupos. Então, Max Pooling sobreposto \(3 \times 3\) (stride: 2)
- Saídas: \(13 \times 13 \times 128\) mapas de características \(\times 2\) grupos Então, Normalização de Resposta Local
- Saídas: \(13 \times 13 \times 128\) mapas de características \(\times 2\) grupos
Redes Neurais Convolucionais
Vamos entender a arquitetura da AlexNet

3ª: Camada Convolucional: 2 grupos de 192 kernels de tamanho \(3 \times 3 \times 256\) (stride: 1, pad: 1)
Saídas: \(13 \times 13 \times 192\) mapas de características \(\times 2\) grupos.
4ª: Camada Convolucional: 2 grupos de 192 kernels de tamanho \(3 \times 3 \times 192\) (stride: 1, pad: 1)
Saídas: \(3 \times 13 \times 192\) mapas de características \(\times 2\) grupos
Redes Neurais Convolucionais
Vamos entender a arquitetura da AlexNet

- 5ª: Camada Convolucional: 256 kernels de tamanho \(3 \times 3 \times 192\) (stride: 1, pad: 1)
- Saídas: \(13 \times 13 \times 128\) mapas de características \(\times 2\) grupos. Então, Max Pooling sobreposto \(3 \times 3\) (stride: 2)
- Saídas: \(6 \times 6 \times 128\) mapas de características \(\times 2\) grupos.
Redes Neurais Convolucionais
Vamos entender a arquitetura da AlexNet

6ª: Camada Totalmente Conectada (Densa) de 4096 neurônios
7ª: Camada Totalmente Conectada (Densa) de 4096 neurônios
Redes Neurais Convolucionais
Vamos entender a arquitetura da AlexNet

8ª: Camada Totalmente Conectada (Densa) de 1000 neurônios (saída) Saídas: 1000 neurônios (já que existem 1000 classes)
Softmax é usado para calcular a perda.
No total, há 60 milhões de parâmetros que precisam ser treinados!!!
OBRIGADO!
Slide produzido com quarto

Referências CNN
Hubel, D. H., & Wiesel, T. N. (1962). Receptive fields, binocular interaction and functional architecture in the cat’s visual cortex. Journal of Physiology.
Goodfellow, I., Bengio, Y., & Courville, A. (2016). Deep Learning. MIT Press.
https://www.datacamp.com/tutorial/introduction-to-convolutional-neural-networks-cnns
Yann Lecun, Lon Bottou, Yoshua Bengio, and Patrick Haffner. Gradient-based learning applied to document recognition. In Proceedings of the IEEE, pages 2278–2324, 1998.
https://towardsdatascience.com/review-senet-squeeze-and-excitation-network-winner-of-ilsvrc-2017-image-classification-a887b98b2883
https://arxiv.org/pdf/1603.07285
Referências para serem utilizadas
BRAGA, A. P.; CARVALHO, A.; LUDEMIR, T. Redes Neurais Artificiais: Teoria e Aplicações. .: [s.n.], 2000.
HOPFWELD, J. J. Neural networks and physical systems with emergent collective computational abilities. Proc. NatL Acad. Sci., v. 79, p. 2554–2558, 1982.
LUDWIG, O.; MONTGOMERY, E. Redes Neurais - Fundamentos e Aplicações com Programas em C. .: Ciência Moderna, 2007.
MINSKY, M.; PAPERT, S. Perceptrons: an introduction to computationational geometry. [S.l.]: MIT Press, 1969.
PINHEIRO, C. A. R. Inteligência Analítica: Mineração de Dados e Descoberta de Conhecimento. .: [s.n.], 2008.
RICH, E.; KNIGHT, K. Inteligência Artificial. .: [s.n.], 1993.
ROSENBLATT, F. Principles of Neurodynamics: Perceptrons and Theory of Brain Mechanisms. .: Washigton, DC, 1962.
OBRIGADO!
Slide produzido com quarto
Tópicos Especiais em Estatística Comp. - Prof. Jodavid Ferreira