Tópicos Especiais em Estatística Comp.

Dropout

Prof. Jodavid Ferreira

UFPE

Dropout

Foi introduzida por Geoffrey Hinton em 2012 e é amplamente utilizada para melhorar a capacidade de generalização dos modelos.

O Dropout é uma técnica de regularização usada em redes neurais para prevenir o overfitting.

Overfitting é um problema comum em redes neurais, onde o modelo se ajusta excessivamente aos dados de treinamento e perde a capacidade de generalizar para novos dados.

Isso acontece porque a rede pode se tornar muito complexa e memorizar os padrões do conjunto de treinamento. O Dropout ajuda a mitigar esse problema introduzindo uma forma de “ruído” durante o treinamento.

Dropout

Quando se trata de combater o overfitting, o dropout definitivamente não é a única opção. Existem outras técnicas, como por exemplo:

Parada antecipada: interromper o treinamento automaticamente quando uma medida específica de desempenho (por exemplo, perda de validação, acurácia) parar de melhorar.
Decaimento de peso: incentivar a rede a usar pesos menores adicionando uma penalidade à função de perda (isso garante que as normas dos pesos sejam distribuídas de forma relativamente uniforme entre todos os pesos na rede, o que impede que apenas alguns pesos influenciem fortemente a saída da rede).

Dropout

Ruído: permitir algumas flutuações aleatórias nos dados através da augmentação (o que torna a rede robusta a uma maior distribuição de entradas e, portanto, melhora a generalização).
Combinação de modelos: fazer a média das saídas de redes neurais treinadas separadamente (requer muito poder computacional, dados e tempo).

Apesar da abundância de alternativas, o dropout continua sendo uma medida protetora extremamente popular contra o overfitting por causa de sua eficiência e eficácia.

Dropout

A ideia básica do Dropout é desligar (ou “drop”) aleatoriamente uma fração dos neurônios durante o treinamento, o que força a rede a não depender de neurônios específicos, mas sim a aprender representações mais robustas dos dados.

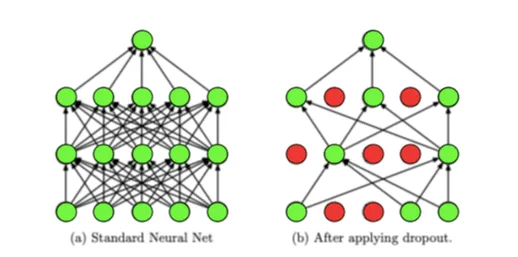
Isso previne que as unidades se adaptem excessivamente umas às outras.

Dropout

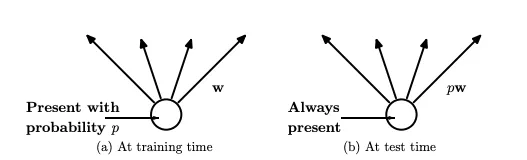
Durante o treinamento, em cada iteração, cada neurônio tem uma probabilidade \(p\) de ser “desligado”.

Isso significa que as ativações desses neurônios são temporariamente removidas da rede, juntamente com suas conexões.

Essa técnica é aplicada apenas durante o treinamento; na fase de inferência (teste), todos os neurônios estão ativos, mas suas saídas são escaladas por \(p\) para manter a consistência das ativações.

Dropout

Como o dropout remove algumas das unidades de uma camada, uma rede com dropout ponderará as unidades restantes mais fortemente durante cada execução de treinamento para compensar as entradas ausentes.
No entanto, no momento do teste, não é viável usar os pesos do modelo treinado em seus estados exagerados e, portanto, cada peso é reduzido multiplicando-se pelo hiperparâmetro \(p\).

Esse fenômeno pode ser observado no exemplo abaixo.

Vamos observar uma rede com quatro unidades em uma camada (imagem abaixo). O peso em cada unidade será inicialmente \(\dfrac{1}{4} = 0.25\).

Dropout

Se aplicarmos dropout com \(p = 0.5\) a essa camada, ela poderia acabar se parecendo com a seguinte imagem:

Como podemos ver, duas unidades foram “desligadas” aleatoriamente.
Isso significa que as conexões dessas unidades foram removidas temporariamente da rede.
Como apenas duas unidades são consideradas, cada uma terá um peso inicial de \(\dfrac{1}{2} = 0.5\).

Dropout

No entanto, o dropout é usado apenas no treinamento, então não queremos que esses pesos fiquem fixos nesse valor alto durante o teste.
Para resolver esse problema, quando passamos para a fase de teste, multiplicamos os pesos por \(p\) (como visto na imagem abaixo), terminando com \(0.5*0.5 = 0.25\), que nesse caso, coincidentemente foi igual ao peso inicial correto.

Dropout

Configurações de hiperparâmetros que têm se mostrado eficazes com a regularização por dropout incluem uma alta taxa de aprendizado decrescente e um alto momento. Isso se deve a alguns fatores específicos:

Alta Taxa de Aprendizado Decrescente: A taxa de aprendizado determina o tamanho dos passos que o algoritmo de otimização dá na direção dos gradientes. Uma alta taxa de aprendizado permite que o modelo faça ajustes significativos nos pesos em cada iteração, acelerando o processo de treinamento. No entanto, taxas de aprendizado muito altas podem causar oscilações nos pesos ou mesmo impedir a convergência. Quando usamos dropout, a regularização ajuda a evitar que os pesos “explodam” (aumentem descontroladamente), permitindo assim que possamos usar uma alta taxa de aprendizado sem esses riscos. À medida que o treinamento progride, a taxa de aprendizado pode ser reduzida gradualmente (decrescente), o que ajuda o modelo a se estabilizar e ajustar finamente os pesos.

Dropout

Alto Momento: O momento é um hiperparâmetro que ajuda a acelerar o gradiente descendente em direção ao mínimo ótimo, suavizando o processo de otimização. Ele faz isso acumulando uma fração das atualizações passadas para determinar a direção da atualização atual. Um alto momento significa que as atualizações são mais influenciadas pelas direções anteriores, ajudando a atravessar platôs e evitando que o algoritmo fique preso em mínimos locais. Com o dropout, o uso de um alto momento é benéfico porque o ruído introduzido pelo dropout pode ser compensado pelo efeito estabilizador do momento.

Dropout

Exploração de Diferentes Regiões da Função de Perda: O dropout introduz ruído durante o treinamento ao desligar aleatoriamente unidades na rede. Esse ruído, em conjunto com uma alta taxa de aprendizado, permite que o modelo explore diferentes regiões da função de perda. Isso pode ajudar o modelo a escapar de mínimos locais e encontrar um ponto de convergência melhor, potencialmente levando a um desempenho superior.

Portanto, a combinação de uma alta taxa de aprendizado decrescente e um alto momento, junto com a regularização por dropout, pode melhorar significativamente a eficácia do treinamento de redes neurais, resultando em modelos mais robustos e com melhor capacidade de generalização.

Dropout

Desvantagem do Dropout

O dropout pode aumentar o tempo de treinamento, pois a rede precisa ser treinada várias vezes com diferentes subconjuntos de neurônios desligados.

No entanto, o aumento do tempo de treinamento é geralmente compensado pela melhoria na capacidade de generalização do modelo.

Complexidade adicional em determinar a taxa de Dropout ideal pode requerer experimentação adicional.

O Dropout pode não ser tão eficaz em redes neurais profundas, onde o overfitting é mais comum, pois a remoção aleatória de neurônios pode não ser suficiente para regularizar a rede adequadamente.

Referências para serem utilizadas

BRAGA, A. P.; CARVALHO, A.; LUDEMIR, T. Redes Neurais Artificiais: Teoria e Aplicações. .: [s.n.], 2000.

HOPFWELD, J. J. Neural networks and physical systems with emergent collective computational abilities. Proc. NatL Acad. Sci., v. 79, p. 2554–2558, 1982.

LUDWIG, O.; MONTGOMERY, E. Redes Neurais - Fundamentos e Aplicações com Programas em C. .: Ciência Moderna, 2007.

MINSKY, M.; PAPERT, S. Perceptrons: an introduction to computationational geometry. [S.l.]: MIT Press, 1969.

PINHEIRO, C. A. R. Inteligência Analítica: Mineração de Dados e Descoberta de Conhecimento. .: [s.n.], 2008.

RICH, E.; KNIGHT, K. Inteligência Artificial. .: [s.n.], 1993.

ROSENBLATT, F. Principles of Neurodynamics: Perceptrons and Theory of Brain Mechanisms. .: Washigton, DC, 1962.

OBRIGADO!

Slide produzido com quarto