Tópicos Especiais em Estatística Comp.
Redes Neurais Artificiais e MLP
UFPE
Introdução
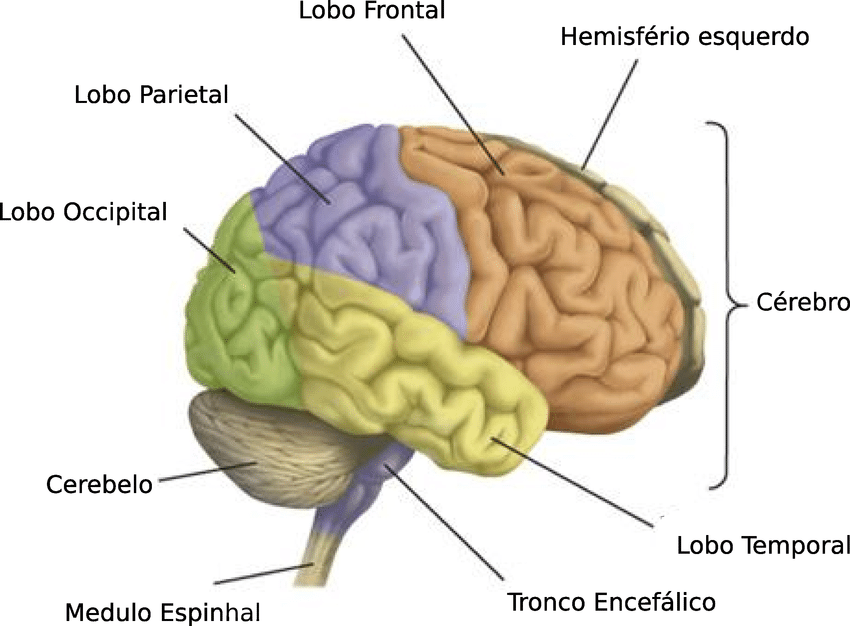
O cérebro é o mais requintado dos instrumentos, capaz de refletir as complexidades e os emaranhamentos do mundo ao nosso redor.
Centro da inteligência, memória, consciência e linguagem, o cérebro controla, em colaboração com outras partes do encéfalo, as sensações e os órgãos efetores, ele é o ponto mais alto da evolução, o único órgão consciente da sua existência.
Introdução
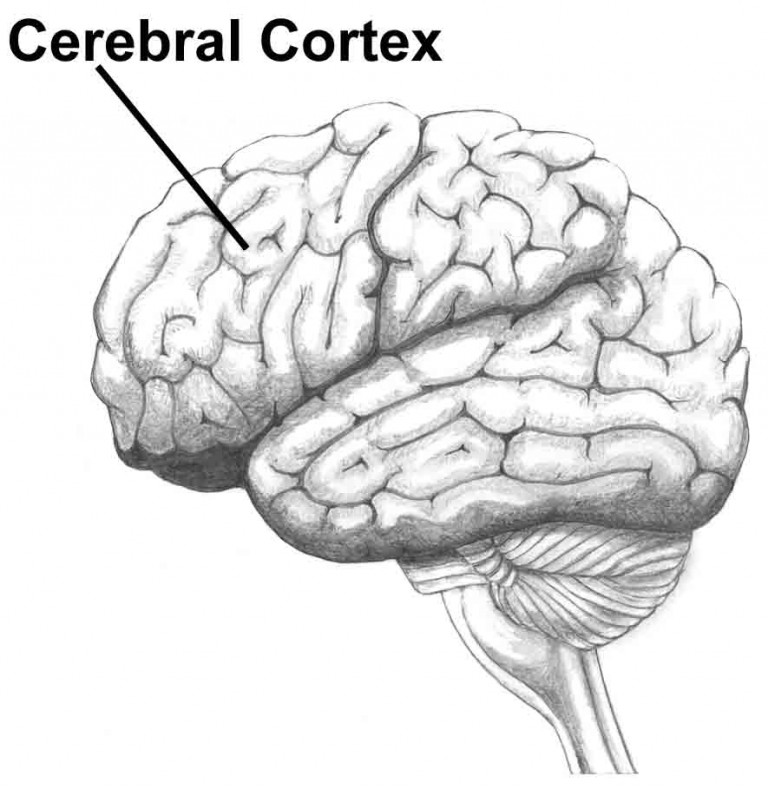
O córtex cerebral é a fina camada de substância cinzenta que reveste o centro branco medular de todo encéfalo e possui uma espessura que varia de 1 a 4 mm.
Trata-se de uma das partes mais importantes do sistema nervoso e a maior parte é composta por células nervosas (neurônios) que recebem impulsos dos pontos mais distantes do corpo e os retransmitem ao destino certo.
Introdução
No córtex cerebral chegam impulsos provenientes de todas as vias da sensibilidade que aí se tornam conscientes e são interpretadas.
Do córtex saem os impulsos nervosos que iniciam e comandam os movimentos voluntários e involutários. Com ele estão relacionados os fenômenos psíquicos como a memória, a inteligência, a linguagem e a consciência.
- Memória: capacidade de armazenar e recuperar informações.
- Inteligência: capacidade de raciocinar, planejar, resolver problemas, pensar de forma abstrata, compreender ideias complexas, aprender rapidamente e aprender com a experiência.
- Linguagem: capacidade de se comunicar por meio de sinais orais, escritos ou gestuais.
- Consciência: capacidade de perceber a si mesmo e ao ambiente.
Introdução
Sabendo que o Córtex Cerebral é formado em sua maior parte por Neurônios, vamos entender um pouco mais sobre eles!
Introdução
Neurônio:
- O neurônio é a unidade fundamental do cérebro e tem como função básica receber, processar e enviar informações. Ou seja, transmitir os impulsos nervosos
- O número de neurônios é fixo e não se multiplicam.
- Durante o desenvolvimento intra-uterino, o cérebro humano produzirá todas as células nervosas que o acompanharão durante a vida.
- Estima-se que o cérebro humano possui aproximadamente 86 bilhões de neurônios.
- Cada neurônio pode ter de 1.000 até 10.000 conexões sinápticas.
Introdução - Neurônio
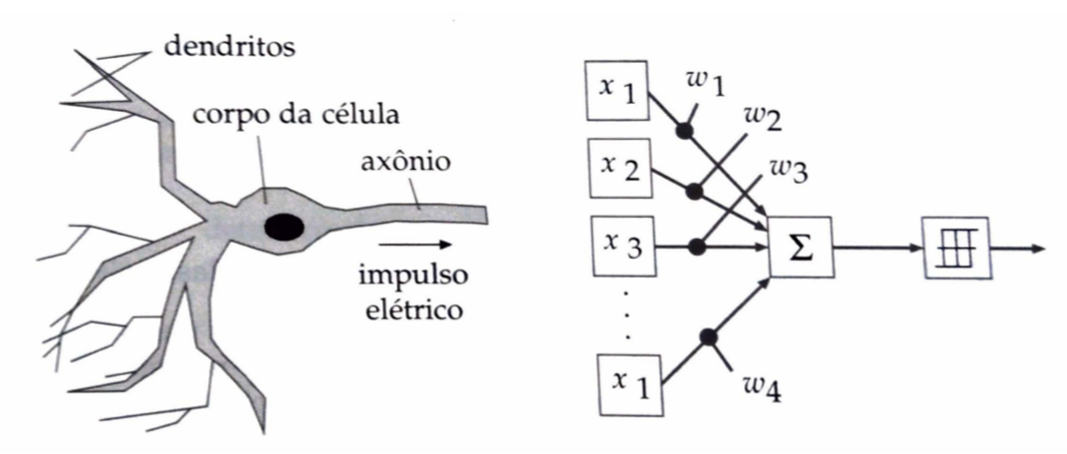
Em geral os neurônios constituem-se dos mesmos compontes básicos:
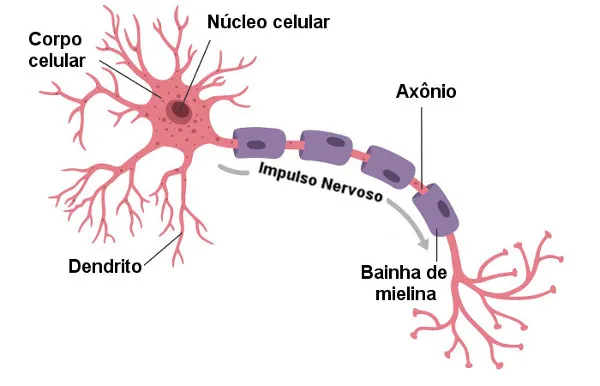
Corpo celular: contém o núcleo e a maioria dos organelos celulares.
Dendritos: prolongamentos que recebem sinais de outros neurônios e levam o impulso nervoso até o corpo celular, sendo, na maioria das vezes, responsáveis pela comunicação entre os neurônios através das sinapses.
Axônio: prolongamento que transmite sinais para outros neurônios. É responsável pela condução do impulso nervoso para o próximo neurônio
Bainha de Mielina: protege o axônio e acelera a transmissão de sinais.
Introdução - Neurônio
A região de contato entre o fim do axônio de um neurônio e os dendritos de outro neurônio é chamado de Sinapse;
A sinapse é composta por:
Botão sináptico: extremidade do axônio que libera neurotransmissores;
Fenda sináptica: espaço entre o botão sináptico e os dendritos;
Receptor: proteína localizada na membrana do dendrito que recebe os neurotransmissores.
O axônio leva os impulsos para fora do corpo celular, as extremidades de cada axônio chegam até bem próximo dos dendritos do próximo neurônio, mas não chega a tocá-lo, ou seja, os neurônios não tem uma ligação física entre eles, mas os mediadores químicos são passados de um neurônio a outro.
Introdução - Neurônio
Redes Neurais Artificiais
Redes Neurais Artificiais são estruturas computacionais inspiradas no sistema nervoso de seres vivos, mais especificamente neurônios. Porém aqui devem ser guardadas as proporções:
enquanto as redes neurais biológicas estão entre as estruturas mais complexas já conhecidas e seu funcionamento ainda não é totalmente compreendido,
as Redes Neurais Artificiais buscam simular o comportamento dos neurônios para executar apenas tarefas bem específicas, como as de classificar um objeto.
- As redes neurais artificiais são sistemas paralelos distribuídos compostos por unidades de processamento simples (nodos) que calculam determinadas funções matemáticas (normalmente não-lineares).
Redes Neurais Artificiais
As redes neurais são semelhantes ao funcionamento do cérebro humano em dois aspectos fundamentais:
o conhecimento é adquirido pela rede neural por meio de um processo de aprendizado
e os pesos das conexões entre neurônios, conhecidas como sinapses, são utilizados para armazenar o conhecimento.
O procedimento utilizado para representar o processo de aprendizado, normalmente conhecido como algoritmo de aprendizado, é uma função para modificar os pesos das conexões da rede com o objetivo de alcançar um valor previamente estabelecido.
Redes Neurais Artificiais
- As redes neurais aprendem a identificar os padrões de uma determinada base de dados por meio da análise dos seus respectivos casos, construindo um mapeamento de entrada e saída analogamente aos ,modelos estatísticos não paramétricos.
- Dessa forma, os modelos de redes neurais podem identificar padrões que são evidentes ou característicos para um problema em particular e armazenar esse conhecimento com uma base de inferência para classificação ou predição.
- O conhecimento é representado em uma rede neural pela sua própria estrutura e pelo estado de ativação e pode se adaptar às menores mudanças nas situações utilizadas como base de aprendizado.
Redes Neurais Artificiais
Conceitualmente, uma rede neural artificial consiste de um conjunto de componentes de processamento interconectados entre si, formando uma rede.

Redes Neurais Artificiais
Conceitualmente, uma rede neural artificial consiste de um conjunto de componentes de processamento interconectados entre si, formando uma rede.
Redes Neurais Artificiais
Uma unidade da rede é chamada de neurônio, assim como no sistema nervoso humano, e as conexões entre essas unidades são chamadas de sinapses, seguindo a mesma analogia.
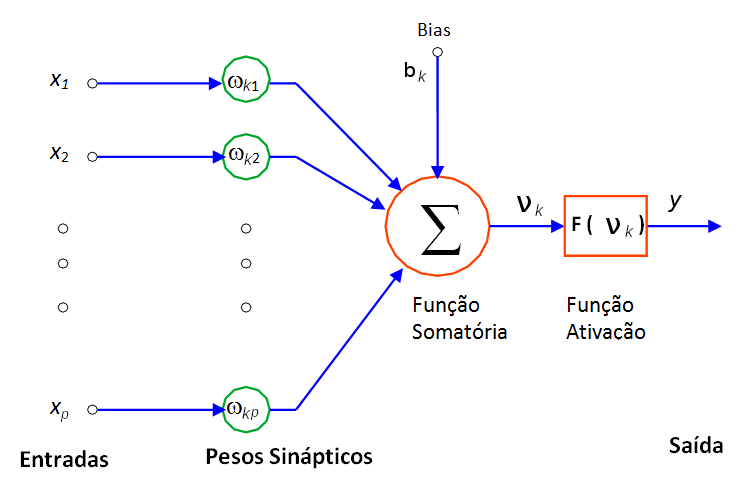
Redes Neurais Artificiais

O componente central de uma rede neural é o neurônio, ou nó. O neurônio recebe um conjunto de informações de entrada \(x_j\) a partir de outros nós, e multiplica cada entrada por um peso \(w_{kj}\), que está associado a cada uma das conexões.
O produto resultante dessa multiplicação é somado dentro do neurônio para gerar uma ativação \(\nu_k = \sum_{j=1}^p x_j w_{kj}\).
A ativação é transformada utilizando-se uma função de transferência \(F(\nu_k)\) para produzir a saída do nó.
Usualmente, uma função de transferência sigmoidal do tipo \(F(\nu_k) = 1 / (1 + e^{-\nu_k})\) é utilizada, onde \(\nu_k\) é a ativação.
Redes Neurais Artificiais
Redes Neurais Artificiais
Conforme visto anteriormente, a saída do neurônio é calculada a partir das entradas ponderadas por um peso associado a conexão.
\[\varphi_k=F(\nu_k) = F\left(\sum_{j=1}^p x_j w_{kj}\right)\]
\(x_j\) é a entrada do neurônio da \(j\)-ésima variável, ou valor de observação, \(w_{kj}\) é o peso da conexão na \(k\)-ésima camada da \(j\)-esima variável, \(\nu_k\) é o valor da ativação e \(F(\cdot)\) é a função de ativação.
Diversas funções de ativação podem ser utilizadas na implementação de uma rede neural em multicamadas.
Redes Neurais Artificiais
As funções de ativação mais básicas são a função linear:
\[\varphi_k=F(\nu_k) = \nu_k = \sum_{j=1}^p x_j w_{kj},\] 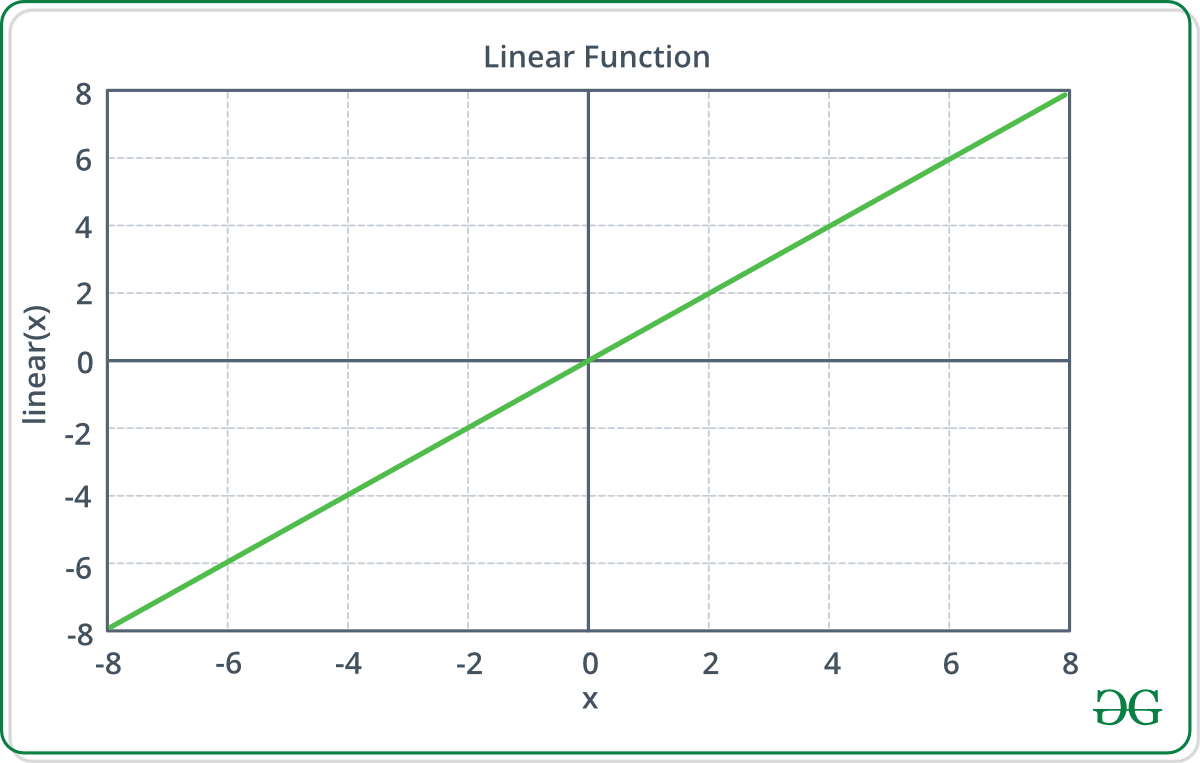
a função lógica, ou de ativação por limiar (também conhecida como função degrau):
\[\begin{align} %\begin{eqnarray} \varphi_k = F(\nu_k) =\left\{ \begin{array}{c l} 0, & \nu_k < \beta\\ 1, & \nu_k > \beta \end{array}\right. %\end{eqnarray} \end{align}\]
\(\beta\) é o ponto de transição do neurônio. Nesse caso, o ponto de transição pode ser incorporado ao neurônio, o que resulta em uma função da seguinte forma:
\[\varphi_k=F(\nu_k) = F \left( \sum_{j=1}^p x_j w_{kj} + \beta \right)\]
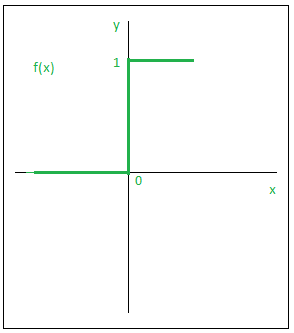
Redes Neurais Artificiais
Entretanto, a função de ativação degrau possui algumas limitações como mapeia valores de entrada para 0 ou 1, tem uma derivada zero quase em todos os lugares, exceto no ponto de mudança (o limiar). Isso faz com que o gradiente seja zero para quase todas as entradas, resultando no “vanishing gradient problem” (problema do gradiente desaparecendo), onde os pesos não são ajustados adequadamente durante o treinamento.
Redes Neurais Artificiais
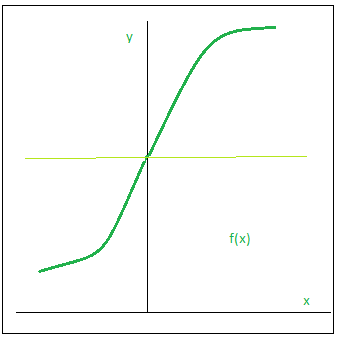
Uma função contínua, que permite a implementação de algoritmos mais complexos para o treinamento da rede, é a função sigmoide:
\[\varphi_k=F(\nu_k) = \dfrac{1}{1+e^{-\alpha \nu_k}}\] onde \(\alpha\) é um parâmetro de ajuste da função, geralmente é utilizado \(\alpha = 1\). A função de ativação sigmoide possui como saída o intervalo [0, 1].
Redes Neurais Artificiais
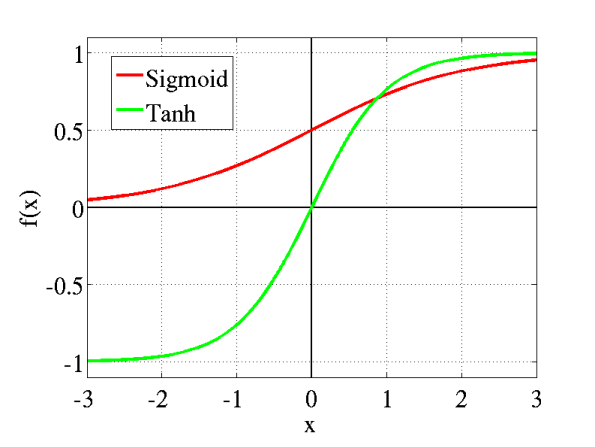
Temos também a função tangente hiperbólica:
\[\varphi_k =F(\nu_k ) = tanh(\nu_k)\]
A função tangente hiperbólica possui como saída o intervalo [-1,1].
Existem outras funções de ativação que podem ser utilizadas, dependendo do problema a ser resolvido e da arquitetura da rede.
Redes Neurais Artificiais
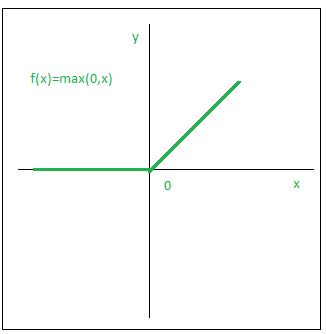
Uma função que está sendo muito utilizada ultimamente é a função de ativação ReLU (Rectified Linear Unit), dada por:
\[\varphi_k =F(\nu_k) = max(0,\nu_k)\]
essa função é muito utilizada em redes neurais profundas, pois acelera o treinamento da rede, devido ao fato da derivada ser constante para valores positivos de \(\nu_k\).
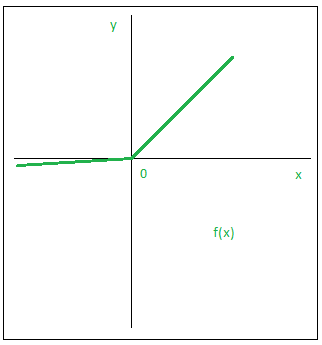
Outra que vem em crescente uso, é a função de ativação Leaky ReLU, dada por:
\[\varphi_k = F(\nu_k) = max(0.01\nu_k,\nu_k)\]
Essa função é uma variação da ReLU, que permite que valores negativos de \(\nu\) sejam passados adiante, o que pode ajudar no treinamento da rede.
Redes Neurais Artificiais
Em geral quando temos um problema de multiclasse utilizamos a função de ativação softmax, que é uma generalização da função sigmoide para múltiplas classes, dada por:
\[\varphi_{kc} = F(\nu_{kc}) = \dfrac{e^{\nu_{c}}}{\sum_{g=1}^{C}e^{\nu_g}}\]
onde \(c\) é o número de classes do problema.
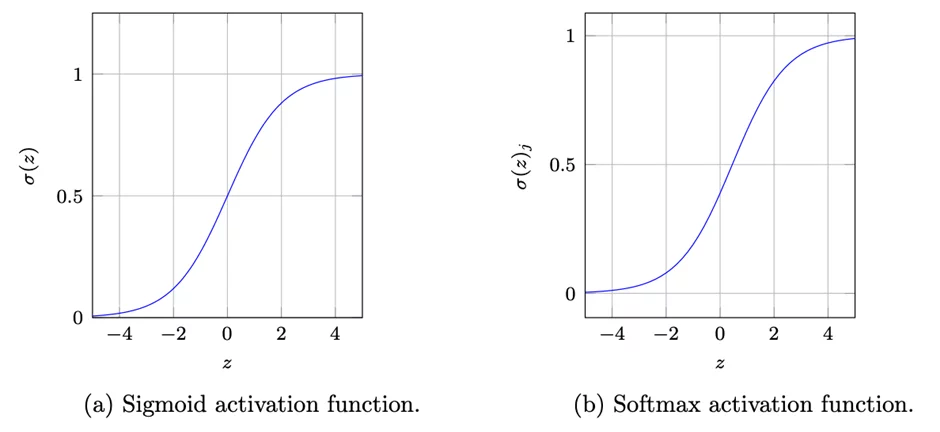
Na Figura (a), acima, \(\sigma (z) = F(\nu_{k})\) e na Figura (b) \(\sigma (z)_j = F(\nu_{kc})\), e \(z = \nu_k\) ou \(z = \nu_{kc}\).
Redes Neurais Artificiais
- O modelo neuronal matemático também pode incluir um viés de entrada, representado pela letra \(b\).
- Esta variável é incluída ao somatório da função de ativação, com o intuito de aumentar a capacidade de aproximação da rede.
- O viés possibilita que um neurônio apresente saída não nula ainda que todas as suas entradas sejam nulas.
Redes Neurais Artificiais
- Por exemplo, caso não houvesse o viés e todas as entradas de um neurônio fossem nulas, então o valor da função de ativação seria nulo.
- Desta forma não poderíamos por exemplo, fazer com que o neurônio aprendesse a relação \(x=[0\, \,0]^\top\) e \(y=1\), pertinente ao problema “ou exclusivo” da lógica.
- O valor do viés é ajustado da mesma forma que os pesos sinápticos.
Redes Neurais Artificiais
Perceptron
O perceptron, invenção de Rosenblatt, é considerado o primeiro modelo de redes neurais.
Dentre os tipos de redes neurais existentes, o perceptron é a arquitetura mais simples, apresentando apenas um neurônio, ou seja, uma única camada.
Redes Neurais Artificiais
Perceptron

Este tipo de rede neural, embora simples, apresenta problemas específicos, não podendo ser utilizada em aplicações mais avançada, apenas em estruturas de decisão simples.
O perceptron modela um neurônio pegando uma soma ponderada de suas entradas e enviando o resultado 1 se a soma for maior que algum valor inicial ajustável ( caso contrário, ele envia o resultado 0).
Redes Neurais Artificiais - Perceptron
- Em um perceptron as conexões são unidirecionais
- As entradas (\(x_1, x_2, \ldots, x_p\)) e os pesos das conexões (\(w_1, w_2, \ldots, w_p\)) na figura são tipicamente valores reais, tanto positivos quanto negativos.
- Se a presença de alguma característica \(x_j\) tender a disparar o perceptron, o peso \(w_j\) será positivo; se a característica \(x_j\) inibir o perceptron, o peso \(w_j\) será negativo.
- E temos que neste caso, a o processo de “aprendizagem” é o processo de modificar os valores dos pesos e do limite.
Redes Neurais Artificiais - Perceptron

Redes Neurais Artificiais - Perceptron
- Apesar de ter causado grande euforia na comunidade científica da época, o perceptron não teve vida muito longa, já que as duras críticas de Minsky e Papert (1969) à sua capacidade computacional causaram grande impacto sobre as pesquisas em RNAs, levando a um grande desinteresse pela área durante os anos 70 e início dos anos 80.
- Essas críticas são relacionadas a um problema denominado de problema da linearidade, que é a incapacidade do perceptron de resolver problemas não-lineares. Um exemplo clássico é o problema do XOR, que vamos apresentar a seguir.
Redes Neurais Artificiais - Perceptron
Problema do XOR
- A disjunção exclusiva ou XOR (escrito como \(\oplus\), \(+\), ou ainda \(\neq\)) é uma operação sobre dois ou mais valores lógicos, tipicamente os valores de duas proposições, que produz um valor verdadeiro apenas se a quantidade de operadores verdadeiros for ímpar.
Tabela da Verdade
A tabela de verdade para p XOR q de duas entradas é a seguinte:
| p | q | p \(\oplus\) q |
|---|---|---|
| F | F | F |
| F | V | V |
| V | F | V |
| V | V | F |
Redes Neurais Artificiais - Perceptron
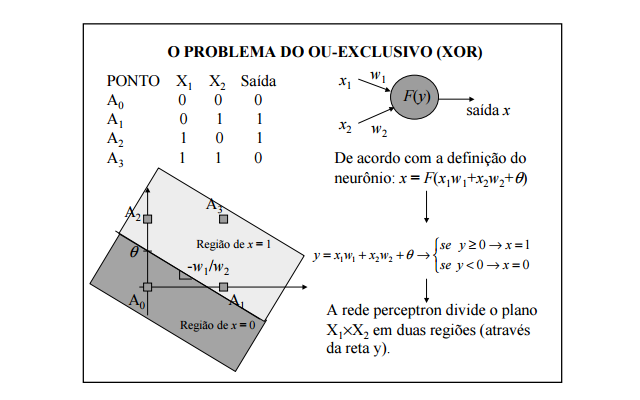
mudando-se os valores de \(w_1\) e \(w_2\) e \(\theta\), muda-se a inclinação e a posição da reta;
entretanto é impossível achar uma reta que divide o plano de forma a separar os pontos \(A_1\) e \(A_2\) de um lado e \(A_0\) e \(A_3\) do outro.
redes de uma única camada só representam funções linearmente separáveis.
Redes Neurais Artificiais - Perceptron
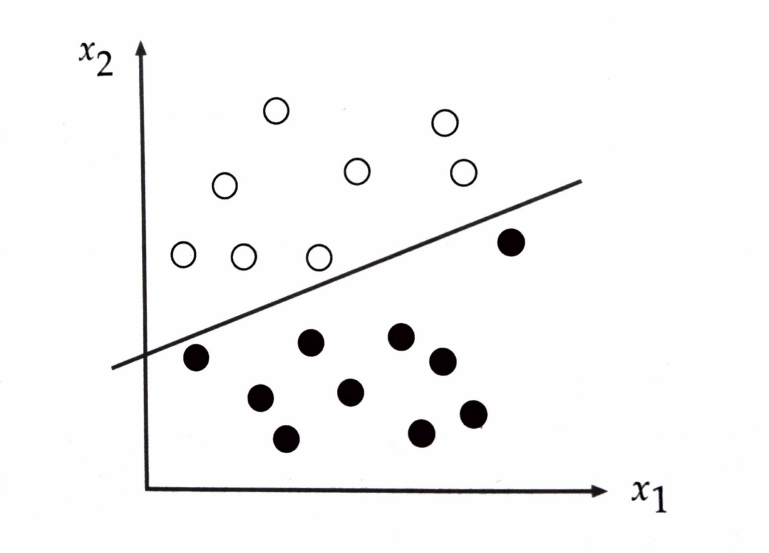
Exemplo de problema linearmente separável
- Considere o problema da classificação de padrões mostrado na Figura a seguir. Este problema é separável linearmente, porque podemos desenhar uma linha que separa uma classe da outra.
Redes Neurais Artificiais - Perceptron
- Esta visão pessimista da capacidade do perceptron e das Redes Neurais Artificiais de uma maneira geral mudou com as descrições da rede de e Hopfweld (1982) e e do algoritmo backpropagation em 1986.
- Foi em consequência destes trabalhos que a área de Redes Neurais Artificiais ganhou novo impulso, ocorrendo, a partir do final dos anos 80, uma forte expansão no número de trabalhos de aplicação e teóricos envolvendo Redes Neurais Artificiais e técnicas correlatas.
Redes Neurais Artificiais
Perceptrons de Múltiplas Camadas (MLP)
Redes Neurais Artificiais
Perceptrons de Múltiplas Camadas (MLP)
- As redes de uma só camada resolvem apenas problemas linearmente separáveis.
- A solução de problemas não linearmente separáveis passa pelo uso de redes com uma ou mais camadas intermediárias ou escondidas.
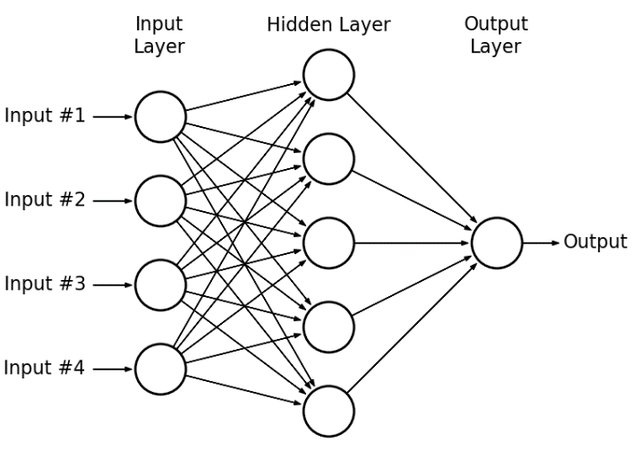
Redes Neurais Artificiais - MLP
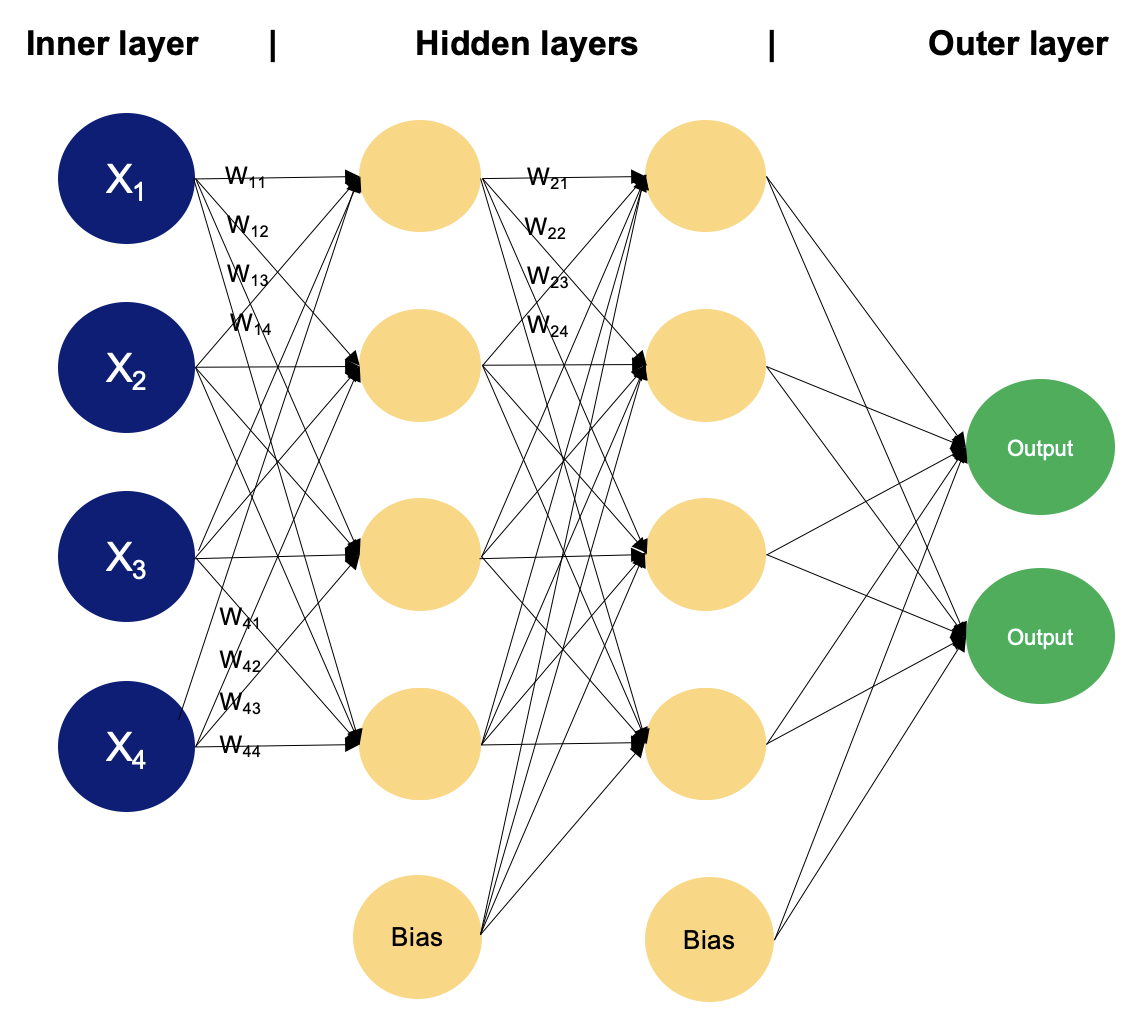
O perceptron de múltiplas camadas ou multilayer perceptron (MLP) é uma rede com uma camada de entrada, que possui a quantidade de nós de entrada iguais a quantidade de features (variáveis) dos dados, uma ou mais camadas ocultas de neurônios e uma camada de saída com um número igual a quantidade desejada dado o problema.
No MLP, o sinal de entrada se propaga para frente (esquerda para direita) através das camadas até a camada de saída, ou seja, é uma rede alimentada para frente, conhecida como feedfoward.
Redes Neurais Artificiais - MLP
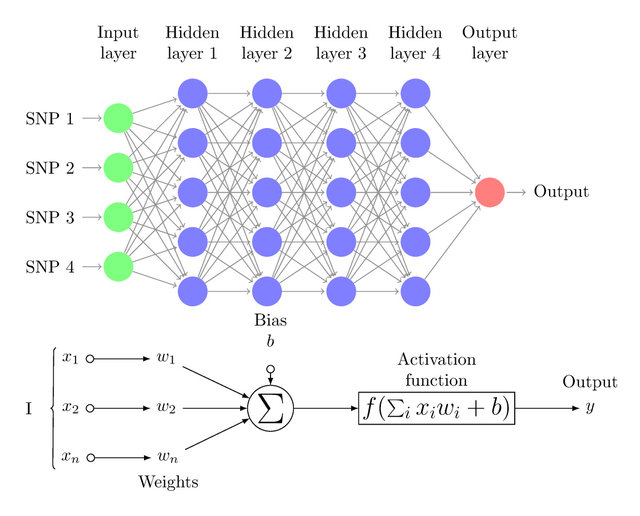
O MLP é uma generalização do perceptron e é treinada de forma supervisionada.
O mecanismo utilizado para a aprendizagem do MLP, é conhecido como algoritmo de retropropagação de erro (backpropagation).
De maneira similar ao perceptron, o MLP necessita da definição da funçã de erro e da taxa de aprendizagem.
Redes Neurais Artificiais - MLP
- Algumas especificidades são atribuídas ao erro.
Todo o procedimento do treinamento do MLP é baseado no erro.
No MLP, o erro do neurônio de saída \(1_{saida}\), na iteração \(t\), é definido por:
\[e_{1_{saida}}(t) = y - \hat{y}(t),\]
em que, \(1_{saida}\) representa o neurônio na camada \({saida}\), camada de saída, \(\hat{y}(t)\) é o valor predito e \(y\) é a resposta real.
Redes Neurais Artificiais - MLP
Considerando uma única observação, o de “erro global” e ou “erro global instantâneo” da rede, é dado por:
\[E(t) = L(\mathbf{y}, \hat{\mathbf{y}}(t)),\]
em que:
- \(L(\mathbf{y}, \hat{\mathbf{y}}(t)) = \dfrac{1}{2} \left( y_{1_{saida}} - \hat{y}_{1_{saida}}(t) \right)^2\), perda quadrática, no contexto de regressão com uma única variável de saída;
- \(L(\mathbf{y}, \hat{\mathbf{y}}(t)) = - \left[ y_{1_{saida}} \log(\hat{y}_{1_{saida}}(t)) + (1 - y_{1_{saida}}) \log(1 - \hat{y}_{1_{saida}}(t)) \right]\), entropia cruzada, no contexto de classificação binária.
Redes Neurais Artificiais - MLP
Se a camada de saída contém \(K_{saida}\) neurônios na iteração \(t\), então:
\[E(t) =\dfrac{1}{2} \sum\limits_{k_{saida}=1}^{K_{saida}} e_{k_{saida}}^2(t).\]
em que: \[e_{k_{saida}}^2(t) = \left( y_{k_{saida}} - \hat{y}_{k_{saida}}(t) \right)^2.\]
E para classificação multiclasse, temos:
\[E(t) = - \sum\limits_{k_{saida}=1}^{K_{saida}} \left[ y_{k_{saida}} \log(\hat{y}_{k_{saida}}(t)) + (1 - y_{k_{saida}}) \log(1 - \hat{y}_{k_{saida}}(t)) \right]\]
Redes Neurais Artificiais - MLP
Quando analisado no contexto de uma amostra de tamanho \(n\), temos que o erro global total é dado por:
\[E_{total}(t) = \dfrac{1}{n}\sum\limits_{i=1}^{n} E_i(t).\]
O erro global total, assim como, o erro global instantâneo \(E_i(t)\) são funções de todos os parâmetros livres (pesos sinápticos e viés) da rede.
Dessa forma, a questão passa a ser em como atribuir uma parcela de culpa, pelo erro global instantâneo, a cada um dos parâmetros, com finalidade de possibilitar o ajuste destes parâmetros em direção a um erro global mínimo.
Vamos seguir os próximos passos com apenas uma observação, ou seja, \(n=1\).
Redes Neurais Artificiais - MLP
- Para compreendermos, imagine uma rede perceptron de múltiplas camadas com função de ativação sigmoide, na qual são atribuídos valores arbitrários para os pesos e para os vieses inicialmente.

Redes Neurais Artificiais - MLP
- Em seguida, é utilizado o o conjunto de entrada\((\mathbf{x}_{1 \times p})\), os quais resultariam num na saída (\(y\)) que, comparada ao valor predito (\(\hat{y}(t)\)), resultariam no erro global instantâneo \(E(t)\), sendo \(t=0\).

Redes Neurais Artificiais - MLP
- Supondo que desejamos ajustar o peso hipotético \(w(k_{l},k_{g}) = w_{k_l k_g}\), ou seja, um peso \(w\) entre um neurônio \(k_{l}\) (alguma camada oculta \(l\)) e o neurônio \(k_{g}\) (alguma camada oculta \(g\)), em que a camada \(g\) é subsequente a \(l\). Podemos, escrever a equação do erro global instantâneo \(E(t)\) em função de \(w_{k_{l}k_{g}}\) mantendo os outros pesos constantes. Assim, ter-se-ia uma equação com a forma geral vista na equação a seguir:
\[E(t) = \dfrac{1}{2} \left(y - \varphi \left( \sum\limits_{k_{saida} = 1}^{K_{saida}} w_{k_{saida}k_d}\varphi \left( \ldots \varphi \left( \sum\limits_{k_l = 1}^{K_l} w_{k_l k_g} \varphi \left(\ldots \varphi \left( \sum\limits_{k_1 = 1}^{K_1} w_{k_{1}k_{2}} x_j \right) \right) \right) \right) \right) \right)^2 \]

Redes Neurais Artificiais - MLP
Esta equação é composta de somatórios de funções sigmoides aninhados, onde \(y\) representa a saída observada, \(x_j\) representa a observação na \(j\)-ésima variável e \(\varphi\) a função de ativação sigmoide. A representação gráfica teria a forma similar a figura apresentada a seguir:
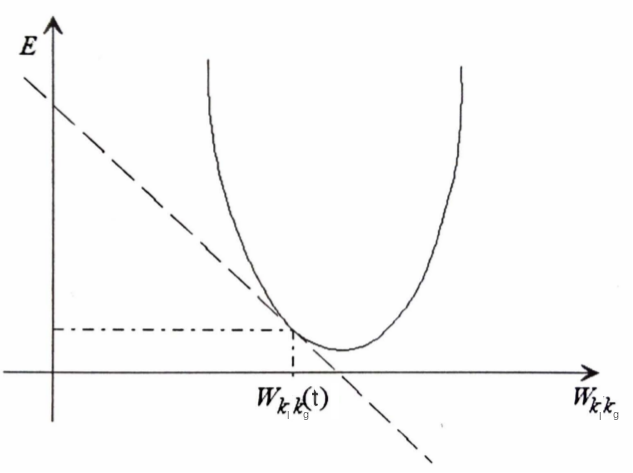
Representação gráfica para o processo de minimização do erro entre \(E \, \times\, w_{k_l k_g}(t)\).
Redes Neurais Artificiais - MLP
- Pelo gráfico temos que uma reta tangente que pode ser obtida por:
\[\dfrac{\partial E(t)}{\partial w_{k_l k_g}(t)}.\]
Essa derivada parcial traz informações sobre o peso \(w_{k_l k_g}(t)\):
se o valor da derivada parcial for positivo, significa que: se for aplicada uma correção positiva ao peso sináptico \(w_{k_l k_g}(t)\), ter-se-ia um acréscimo no erro global \(E(t)\), devendo, neste caso, deve ser aplicada uma correção negativa e vice-versa.
Se o valor da derivada parcial for pequeno, estamos próximos a um \(E(t)\) mínimo para \(w_{k_l k_g}\), devendo assim ser aplicada uma correção a \(w_{k_l k_g}\) pequena.
Redes Neurais Artificiais - MLP
se o valor desta derivada for grande, o valor de \(w_{k_l k_g}\) está distante do valor que resultaria em \(E(t)\) mínimo, portanto seria necessário aplicar uma correção maior para \(w_{k_l k_g}(t)\).
Para corrigir o peso sináptico \(w_{kj}(t)\), utilizamos a regra delta, conforme a equação a seguir:
\[\Delta w_{k_l k_g}(t) = -\eta\dfrac{\partial E(t)}{\partial w_{k_l k_g}(t)},\]
em que \(\eta\) é a taxa de aprendizado.
O processo é repetido até caminhar por todos os pesos e vieses da rede. Em que, após a finalização de uma iteração é dito que foi executado 1 época (epoch).
Redes Neurais Artificiais - MLP
Entretanto, o cálculo da derivada parcial \(\partial E(t)/\partial w_{k_l k_g}(t)\) para cada um dos pesos não é simples, pois, como já foi visto, \(E(t)\) é uma equação composta de somatórios de funções de ativação (\(\varphi\)) aninhados.
\[E(t) = \dfrac{1}{2} \left(y - \varphi \left( \sum\limits_{k_{saida} = 1}^{K_{saida}} w_{k_{saida}k_d}\varphi \left( \ldots \varphi \left( \sum\limits_{k_l = 1}^{K_l} w_{k_l k_g} \varphi \left(\ldots \varphi \left( \sum\limits_{k_1 = 1}^{K_1} w_{k_{1}k_{2}} x_j \right) \right) \right) \right) \right) \right)^2 \]
Como podemos resolver isso?
Redes Neurais Artificiais - MLP
Para nosso entendimento, vamos utilizar como base a estrutura abaixo:
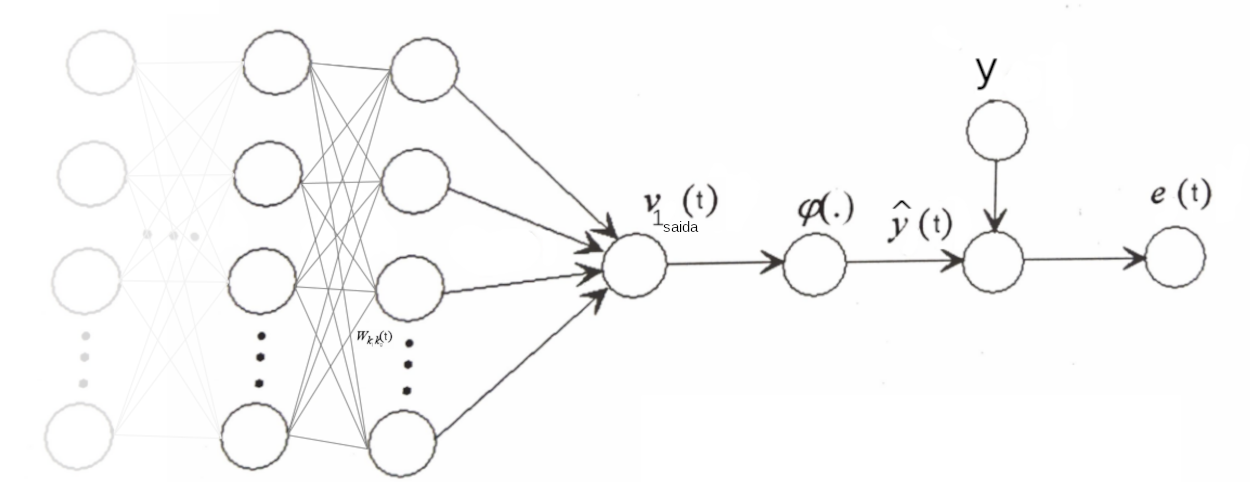
Legenda:
- \(w_{k_l k_g}(t)\): peso sináptico entre o neurônio \(k\) da camada \(l\) e o neurônio \(k\) da camada \(g\) na iteração \(t\);
- \(\nu_{1_{saida}}(t)\): valor de ativação do neurônio \(1\) na camada de \(saida\) na iteração \(t\);
- \(\varphi_{k_g}(\nu_{k_g}(t))\): função de ativação do neurônio \({k_g}\) na camada \(g\) calculado com os neurôrios e da camada \(l\) na iteração \(t\);
- \(\hat{y}_j(t)\): valor predito na iteração \(t\);
- \(y(t)\): valor verdadeiro;
- \(e(t)\): erro obtido na iteração \(t\);
Redes Neurais Artificiais - MLP
Vamos utilizar o Backpropagation
O processo é iniciado pela pela última camada em direção à primeira
são calculados gradientes locais em uma camada, e estes serão utilizados no cálculo dos gradientes de erro da camada imediatamente anterior.
O objetivo será sempre determinar a derivada parcial \(\partial E(t)/\partial w_{k_l k_g}(t)\), para aplicar a correção \(\Delta w_{k_l k_g}(t)\) ao peso sináptico \(w_{k_l k_g}(t)\) ou \(\Delta b_{k_g}(t)\) ao viés \(b_{k_g}(t)\).
Como mencionado anteriormente, o processo é iniciado da camada de saída para as demais camadas anteriores, então, aqui vamos considerar a camada \(d\) como sendo a última camada oculta antes da camada de saída, ou seja, \(k_d\) é o neurônio \(k\) da camada \(d\).
Redes Neurais Artificiais - MLP
De acordo com a regra da cadeia, é possível expressar a derivada parcial como sendo a equação a seguir
\[\begin{equation} \dfrac{\partial E(t)}{\partial w_{k_d k_{saida}}(t)} = \dfrac{\partial E(t)}{\partial e(t)} \dfrac{\partial e(t)}{\partial \hat{y}(t)} \dfrac{\partial \hat{y}(t)}{\partial \nu_{k_{saida}}(t)} \dfrac{\partial \nu_{k_{saida}}(t)}{\partial w_{k_d k_{saida}}(t)}, \label{equacao56} \end{equation}\]
Lembrem-se que \(\hat{y}(t) = \varphi_{k_{saida}}(\nu_{k_{saida}})(t)\).
É importante também definir o gradiente local do neurônio \(k_{saida}\), que é definido por \(\delta_{k_{saida}}(t)\), que é dado pela derivada \(\partial E(t) / \partial \nu_{saida}(t)\), que pode ser escrita como
\[\begin{equation} \delta_{k_{saida}}(t) = \dfrac{\partial E(t)}{\partial \nu_{k_{saida}}(t)} = \dfrac{\partial E(t)}{\partial e(t)} \dfrac{\partial e(t)}{\partial \hat{y}(t)} \dfrac{\partial \hat{y}(t)}{\partial \nu_{k_{saida}}(t)}, \label{equacao57} \end{equation}\]
ou seja, o gradiente é formado pela multiplicação dos três primeiros fatores da função \(\partial E(t) / \partial w_{k_d k_{saida}}(t)\).
Redes Neurais Artificiais - MLP
Vamos desenvolver cada fator da equação:
\[ \dfrac{\partial E(t)}{\partial w_{k_d k_{saida}}(t)} = \color{red}{\dfrac{\partial E(t)}{\partial e(t)}} \dfrac{\partial e(t)}{\partial \hat{y}(t)} \dfrac{\partial \hat{y}(t)}{\partial \nu_{k_{saida}}(t)} \dfrac{\partial \nu_{k_{saida}}(t)}{\partial w_{k_d k_{saida}}(t)}, \]
Temos
\[E(t)=\dfrac{1}{2} e^2(t),\]
logo,
\[ \color{red}{\dfrac{\partial E(t)}{\partial e(t)} = e(t) = y - \hat{y}(t).} \]
Redes Neurais Artificiais - MLP
Desenvolvendo o segundo fator
\[ \dfrac{\partial E(t)}{\partial w_{k_d k_{saida}}(t)} = \dfrac{\partial E(t)}{\partial e(t)} \color{blue}{\dfrac{\partial e(t)}{\partial \hat{y}(t)}} \dfrac{\partial \hat{y}(t)}{\partial \nu_{k_{saida}}(t)} \dfrac{\partial \nu_{k_{saida}}(t)}{\partial w_{k_d k_{saida}}(t)}, \]
em que \(\color{red}{e(t) = y - \hat{y}(t)}\), tem-se:
\[\color{blue}{\dfrac{\partial e(t)}{\partial \hat{y}(t)} = -1,}\]
Redes Neurais Artificiais - MLP
Desenvolvendo o terceiro fator
\[ \dfrac{\partial E(t)}{\partial w_{k_d k_{saida}}(t)} = \dfrac{\partial E(t)}{\partial e(t)} \dfrac{\partial e(t)}{\partial \hat{y}(t)} \color{green}{\dfrac{\partial \hat{y}(t)}{\partial \nu_{k_{saida}}(t)}} \dfrac{\partial \nu_{k_{saida}}(t)}{\partial w_{k_d k_{saida}}(t)}, \]
sendo \(y(t) = \varphi_{k_{saida}}(\nu_{k_{saida}})(t),\) encontra-se
\[\color{green}{\dfrac{\partial \hat{y}(t)}{\partial \nu_{k_{saida}}(t)} = \varphi^\prime_{k_{saida}} (\nu_{k_{saida}})(t).}\]
Se por exemplo, a função de ativação \(\varphi\) for sigmoide \(\left( \varphi_{k_{saida}}(\nu_{k_{saida}}) = \dfrac{1}{1+e^{- \nu_{k_{saida}}}} \right)\), a derivada parcial acima tem a seguinte forma:
\[ \varphi^\prime_{k_{saida}} (\nu_{k_{saida}}) = \dfrac{e^{-\nu_{k_{saida}}}}{(1+e^{-\nu_{k_{saida}}})^2} \]
Redes Neurais Artificiais - MLP
Dado os resultados anteriores, podemos escrever a equação do gradiente local do neurônio \(k_{saida}\), da seguinte forma:
\[\delta_{k_{saida}}(t) = \dfrac{\partial E(t)}{\partial \nu_{k_{saida}}(t)} = \color{red}{\dfrac{\partial E(t)}{\partial e(t)}} \color{blue}{\dfrac{\partial e(t)}{\partial \hat{y}(t)}} \color{green}{\dfrac{\partial \hat{y}(t)}{\partial \nu_{k_{saida}}(t)}} = \color{blue}{-}\color{red}{e(t)}\color{green}{\varphi^\prime_{k_{saida}}(\nu_{k_{saida}})(t)}.\]
E desenvolvendo o quarto fator
\[ \dfrac{\partial E(t)}{\partial w_{k_d k_{saida}}(t)} = \dfrac{\partial E(t)}{\partial e(t)} \dfrac{\partial e(t)}{\partial \hat{y}(t)} \dfrac{\partial \hat{y}(t)}{\partial \nu_{k_{saida}}(t)} \color{orange}{\dfrac{\partial \nu_{k_{saida}}(t)}{\partial w_{k_d k_{saida}}(t)}}, \]
temos que, para o neurônio \(k_{saida}\) com
\[\nu_{k_{saida}}(t) = \sum\limits_{m = 1}^{K_d} w_{m_d k_{saida}} \varphi_{m_d}(\nu_{m_d})(t) \quad \quad \Longrightarrow \quad \quad \color{orange}{\dfrac{\partial \nu_{k_{saida}}(t)}{\partial w_{k_d k_{saida}}} = \varphi_{k_d}(\nu_{k_d})(t).} \]
Redes Neurais Artificiais - MLP
Substituindo os fatores desenvolvidos, temos
\[\begin{align} \dfrac{\partial E(t)}{\partial w_{k_d k_{saida}}(t)} & = \color{red}{\dfrac{\partial E(t)}{\partial e(t)}} \color{blue}{\dfrac{\partial e(t)}{\partial \hat{y}(t)}} \color{green}{\dfrac{\partial \hat{y}(t)}{\partial \nu_{k_{saida}}(t)}} \color{orange}{\dfrac{\partial \nu_{k_{saida}}(t)}{\partial w_{k_d k_{saida}}(t)}} \\ & = \color{blue}{-}\color{red}{e(t)}\color{green}{\varphi^\prime_{k_{saida}}(\nu_{k_{saida}}(t))}\color{orange}{\varphi_{k_d}(\nu_{k_d})(t)} = \delta_{k_{saida}}(t)\color{orange}{\varphi_{k_d}(\nu_{k_d})(t)}. \end{align}\]
Com os resultados anteriores, é possível aplicar a correção a todos os pesos sinápticos e viés dos neurônios.
A correção se dará pela aplicação da regra delta dada por
\[ \Delta w_{k_d k_{saida}}(t) = -\eta \dfrac{\partial E(t)}{\partial w_{k_d k_{saida}}(t)} = -\eta \delta_{k_{saida}}(t)\varphi_{k_d}(\nu_{k_d})(t) \]
em que \(\eta\) é um hiperparâmetro que define a taxa de aprendizado e geralmente é previamente definido pelo usuário.
Redes Neurais Artificiais - MLP
Assim, temos que
\[w_{k_d k_{saida}}(t) = w_{k_d k_{saida}}(t-1) + \Delta w_{k_d k_{saida}}(t)\]
A taxa de aprendizagem \(\eta\) é responsável pela velocidade com que se dá a busca no espaço de pesos, em direção aos valores que resultam em um erro global mínimo.
Quanto menor for a taxa de aprendizagem, mais suave e precisa será a trajetória através do espaços de pesos, entretanto o aprendizado será lento.
Redes Neurais Artificiais - MLP
Vamos agora considerar que temos uma camada \(g\) antecedendo a camada \(d\). Então a derivada parcial para um peso \(w_{k_g k_d}(t)\) pode ser obtido como:
\[\begin{equation} \dfrac{\partial E(t)}{\partial w_{k_g k_d}(t)} = \dfrac{\partial E(t)}{\partial e(t)} \dfrac{\partial e(t)}{\partial \hat{y}(t)} \dfrac{\partial \hat{y}(t)}{\partial \nu_{k_{saida}}(t)} \dfrac{\partial \nu_{k_{saida}}(t)}{\partial \varphi_{k_d}(\nu_{k_d})(t)} \dfrac{\partial \varphi_{k_d}(\nu_{k_d})(t)}{\partial \nu_{k_d}(t)} \dfrac{\partial \nu_{k_d}(t)}{\partial w_{k_g k_d}(t)}, \label{equacao59} \end{equation}\]
entretanto, os três primeiros fatores já foram desenvolvidos anteriormente e correspondem ao gradiente local do neurônio \(k_{saida}\), ou seja, \[\begin{equation} \delta_{k_{saida}}(t) = \dfrac{\partial E(t)}{\partial e(t)} \dfrac{\partial e(t)}{\partial \hat{y}(t)} \dfrac{\partial \hat{y}(t)}{\partial \nu_{k_{saida}}(t)}, \label{equacao60} \end{equation}\]
sendo \(\dfrac{\partial \nu_{k_{saida}}(t)}{\partial \varphi_{k_d}(\nu_{k_d})(t)} = w_{k_d k_{saida}}\), e considerando que a camada de saída pode ser composta por mais de um neurônio, temos que:
Redes Neurais Artificiais - MLP
\[\begin{equation} \delta_{k_{d}}(t) = \varphi^\prime _{k_d}(\nu_{k_d})(t) \sum\limits_{m=1}^{K_{saida}} \delta_{m_{saida}}(t) w_{k_d m_{saida}}(t). \label{equacao62} \end{equation}\]
em que \(\varphi^\prime _{k_d}(\nu_{k_d})(t) = \dfrac{\partial \varphi_{k_d}(\nu_{k_d})(t)}{\partial \nu_{k_d}(t)}\). Sendo assim, podemos reescrever a equação anterior como:
\[\begin{equation} \dfrac{\partial E(t)}{\partial w_{k_g k_d}(t)} = \delta_{k_{d}}(t) \varphi_{k_g}(\nu_{k_g})(t), \label{equacao61} \end{equation}\]
com \(\varphi_{k_g}(\nu_{k_g})(t) = \dfrac{\partial \nu_{k_d}(t)}{\partial w_{k_g k_d}(t)}\). Novamente, a correção neste caso é dado por
\[ \Delta w_{k_g k_{d}} = -\eta \dfrac{\partial E(t)}{\partial w_{k_g k_{d}}(t)} = -\eta \delta_{k_{d}}(t) \varphi_{k_g}(\nu_{k_g})(t) \]
Resumo do processo de treinamento
Perceptrons de Múltiplas Camadas (MLP)
Redes Neurais Artificiais - MLP
Resumo do Processo
Em resumo, o processo backpropagation pode ser descrito em cinco etapas, conforme apresentadas a seguir:
Inicialização: valores são inicializados aleatoriamente aos pesos sinápticos e viés*, geralmente com uma distribuição uniforme, cuja média deverá ser zero.
Propagação dos sinais: aplica-se a camada da rede os dados de entrada \(\mathbf{X}_{n \times p}\) e calcula os valores preditos \(\hat{\mathbf{y}}_{n \times 1}(t)\).
Redes Neurais Artificiais - MLP
Resumo do Processo
Considerando 1 observação de entrada, com \(p\) variáveis.
Em seguida, calcula-se o erro \(e(t)\) pela comparação de \(\hat{y}(t)\) com valor real \(y\).
backpropagation: calculam-se os gradientes locais: \[\delta_{k_{saida}}(t) = -e(t)\varphi'_{k_{saida}}(\nu_{k_{saida}}(t))\]
Redes Neurais Artificiais - MLP
Resumo do Processo
Em seguida, calculam-se os ajustes para os pesos daquela camada, bem como dos viés, os quais devem ser somados aos valores atuais: \[ \Delta w_{k_d k_{saida}} = \eta e(t)\varphi'_{k_{saida}}(\nu_{k_{saida}}(t))\varphi_{k_d}(\nu_{k_d})(t) = \eta \delta_{k_{saida}}(t)\varphi_{k_d}(\nu_{k_d})(t)\] \[ \Delta b_{k_{saida}} = -\eta e(t)\varphi'_{k_{saida}}(\nu_{k_{saida}}(t)) = -\eta \delta_{k_{saida}}(t)\]
O próximo passo é o cálculo do gradiente local para os neurônios da penúltima camada \(g\) antecedente a \(d\) (camada oculta): \[\delta_{k_d}(t) = \varphi'_{k_d}(\nu_{k_d}(t))\sum\limits_{m=1}^{K_{saida}}(\delta_{m_{saida}}(t)w_{k_d m_{saida}}(t)).\]
Redes Neurais Artificiais - MLP
Resumo do Processo
Então, calcula-se o ajuste para todos os pesos que chegam nessa camada de uma camada anterior \(g\) desta camada \(d\), bem como dos viés. \[\Delta w_{k_g k_d} = -\eta \varphi'_{k_d}(\nu_{k_d}(t)) \varphi_{k_g}(\nu_{k_g}(t)) \sum\limits_{m=1}^{K_{saida}}(\delta_{m_{saida}}(t)w_{k_d m_{saida}}(t)) = -\eta \delta_{k_d}(t) \varphi_{k_g}(\nu_{k_g}(t))\] \[\Delta b_{k_g} = -\eta \varphi'_{k_d}(\nu_{k_d}(t)) \sum\limits_{m=1}^{K_{saida}}(\delta_{m_{saida}}(t)w_{k_d m_{saida}}(t)) = -\eta \delta_{k_g}(t)\]
O processo prossegue de forma idêntica para as demais camadas ocultas, assim como para a camada de entrada, em que os valores dos ajustes na primeira camada oculta (após a entrada da rede) deve ter o valor \(\varphi_{k_g}(\nu_{k_g}(t))\) substituído pelo valor de \(x_p\).
Redes Neurais Artificiais - MLP
Resumo do Processo
- Iteração: iteram-se novas épocas para a rede até que seja satisfeito o critério de parada, que pode ser o número máximo de iterações ou um valor limite para o erro global médio da rede.
Tomando como base estes passos, é possível obter uma rede MLP.
Vamos fazer um exemplo.
Redes Neurais Artificiais - MLP
Exemplo
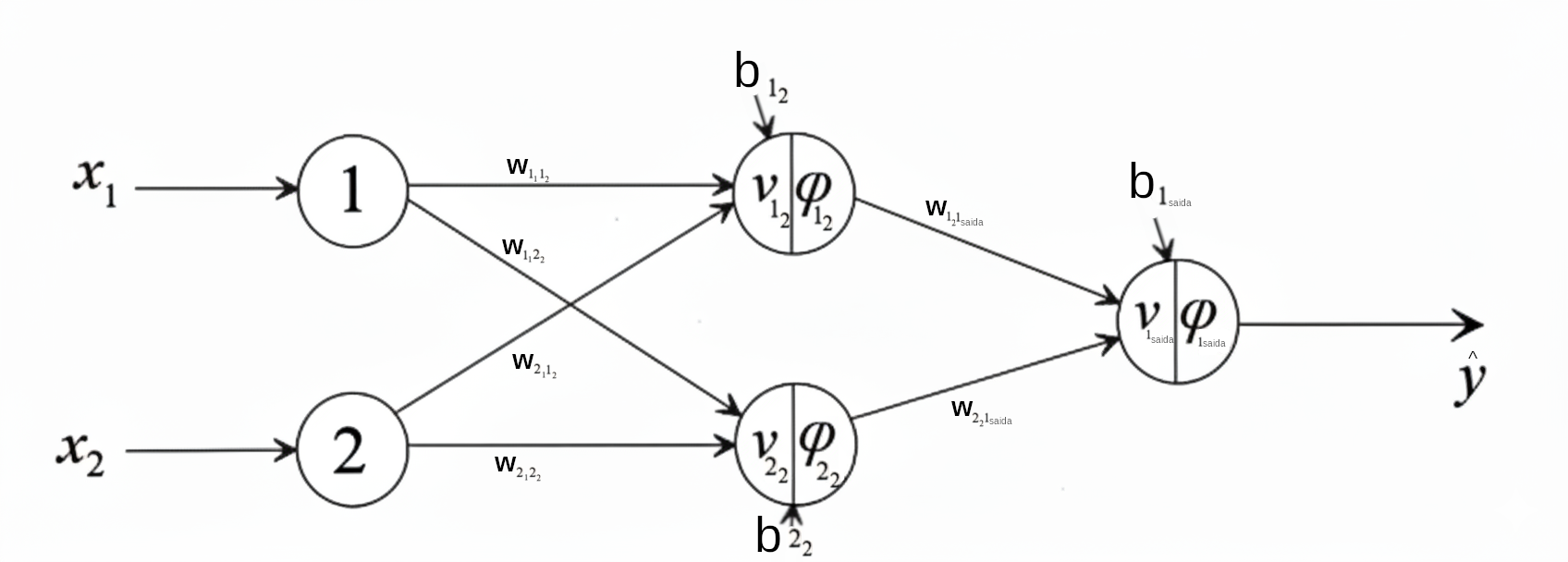
Vamos usar como função de ativação a função sigmoide: \(\varphi(\nu) = \dfrac{1}{1 + e^{-\nu}}\) e os seguintes valores iniciais.
Redes Neurais Artificiais - MLP
Exemplo

Valores de \(\mathbf{x} = [1 \quad 1]\), \(y = 0\), \(\eta = 0.8\), os seguintes pesos e vieses iniciais:
- \(w_{{1_1}{1_2}} = 0.8\)
- \(w_{{1_1}{2_2}} = -0.6\)
- \(w_{{2_1}{1_2}} = 0.3\)
- \(w_{{2_1}{2_2}} = -0.4\)
- \(w_{{1_2}{1_{saida}}} = 0.7\)
- \(w_{{2_2}{1_{saida}}} = -0.8\)
- \(b_{1_2} = 0.7\)
- \(b_{2_2} = -0.4\)
- \(b_{1_{saida}} = -0.3\)
Redes Neurais Artificiais - MLP
Exemplo
Essa primeira iteração é a \(t=0\), vamos ocultar o índice \(t\) para facilitar a notação.
Primeiramente, vamos calcular a primeira iteração da rede, ou seja, o valor predito \(\hat{y}\). As ativações dos neurônios da camada oculta 2:
- \(\nu_{1_2} = w_{{1_1}{1_2}} x_1 + w_{{2_1}{1_2}} x_2 + b_{1_2} = 0.8*1 + 0.3*1 + 0.7 = 1.8\)
- \(\nu_{2_2} = w_{{1_1}{2_2}} x_1 + w_{{2_1}{2_2}} x_2 + b_{2_2} = -0.6*1 + -0.4*1 - 0.4 = -1.4\)
os resultados das funções de ativação são dadas por:
- \(\varphi_{1_2}(\nu_{1_2}) = \dfrac{1}{1 + e^{-1.8}} \approx 0.86\)
- \(\varphi_{2_2}(\nu_{2_2}) = \dfrac{1}{1 + e^{1.4}} \approx 0.20\)
Redes Neurais Artificiais - MLP
Exemplo
Assim, para a próxima camada, temos:
- \(\nu_{1_{saida}} = w_{{1_2}{1_{saida}}} \varphi_{1_2}(\nu_{1_2}) + w_{{2_2}{1_{saida}}} \varphi_{2_2}(\nu_{2_2}) + b_{1_{saida}} \\ \quad\quad\, = 0.7*0.86 + (-0.8)*0.20 - 0.3 \approx 0.14\)
Então,
- \(\hat{y} = \varphi_{1_{saida}}(\nu_{1_{saida}}) = \dfrac{1}{1 + e^{-0.14}} \approx 0.53\)
Lembrando que nosso valor real é \(y = 0\), então o erro nessa iteração \(t=0\) é dado por:
\[e = y - \hat{y} = 0 - 0.53 = -0.53\]
Redes Neurais Artificiais - MLP
Exemplo
Vamos iniciar o processo de backpropagation.
Vamos ajustar o peso \(w_{{1_2}{1_{saida}}}\).
Primeiramente, calculamos o gradiente local do neurônio da camada de saída:
\[\dfrac{\partial E}{\partial w_{{1_2}{1_{saida}}}} = \dfrac{\partial E}{\partial e} \dfrac{\partial e}{\partial \varphi(\nu_{1_{saida}})} \dfrac{\partial \varphi(\nu_{1_{saida}})}{\partial \nu_{1_{saida}}} \dfrac{\partial \nu_{1_{saida}}}{\partial w_{1_2 1_{saida}}},\]
que pode ser escrito como:
\[\dfrac{\partial E}{\partial w_{{1_2}{1_{saida}}}} = \delta_{1_{saida}} \varphi (\nu_{1_2}) = -e\varphi^\prime (\nu_{1_{saida}})\varphi (\nu_{1_{2}}),\]
temos que \(e= 0-0.53 = -0.53\) e \(\varphi (\nu_{1_2}) \approx 0.86\), então
Redes Neurais Artificiais - MLP
Exemplo
\[\varphi^\prime (\nu_{1_{saida}}) = \dfrac{exp(-\nu_{1_{saida}})}{(1 + exp(-\nu_{1_{saida}}))^2} = \dfrac{exp(-0.14)}{(1+exp(-0.14))^2} \approx 0.25\]
Assim, temos um valor de \(\delta_{1_{saida}}\):
\[\delta_{1_{saida}} = -(-0.53)*0.25 \approx 0.13\]
e, portanto,
\[\dfrac{\partial E}{\partial w_{{1_2}{1_{saida}}}} = 0.13*0.86 \approx 0.11,\]
e assim
\[w_{{1_2}{1_{saida}}}(1) = w_{{1_2}{1_{saida}}}(0) + \Delta w_{{1_2}{1_{saida}}} = 0.7 - 0.8*(0.11) \approx 0.61.\]
Redes Neurais Artificiais - MLP
Exemplo
Vamos ajustar agora o peso \(w_{{2_2}{1_{saida}}}\). Utilizando o mesmo procedimento, temos:
\[\dfrac{\partial E}{\partial w_{{2_2}{1_{saida}}}} = \delta_{1_{saida}} \varphi (\nu_{2_2})\]
logo, com \(\varphi (\nu_{2_2}) \approx 0.20\) e \(\delta_{1_{saida}} \approx 0.13\), temos:
\[\dfrac{\partial E}{\partial w_{{2_2}{1_{saida}}}} = 0.13*0.20 \approx 0.03,\]
e assim
\[w_{{2_2}{1_{saida}}}(1) = w_{{2_2}{1_{saida}}}(0) + \Delta w_{{2_2}{1_{saida}}} = -0.8 - 0.8*(0.03) \approx -0.82.\]
Redes Neurais Artificiais - MLP
Exemplo
Ajustando o viés \(b_{1_{saida}}\):
\[\dfrac{\partial E}{\partial b_{1_{saida}}} = \delta_{1_{saida}},\]
pois \(\dfrac{\partial \nu_{1_{saida}}}{\partial b_{1_{saida}}} = 1,\) então
\[\dfrac{\partial E}{\partial b_{1_{saida}}} = 0.13,\]
e
\[b_{1_{saida}}(1) = b_{1_{saida}}(0) + \Delta b_{1_{saida}} = -0.3 - 0.8*(0.13) \approx -0.40.\]
Redes Neurais Artificiais - MLP
Exemplo
Com os valores dos pesos e vieses que estão atualizados, vamos atualizar os pesos da camada anterior. Primeiramente, vamos atualizar o peso \(w_{{1_1}{1_2}}\), que neste caso é
\[\dfrac{\partial E}{\partial w_{{1_1}{1_2}}} = \delta_{1_2} x_1,\]
temos o valor de \(x_1 = 1\), então precisamos calcular o valor de \(\delta_{1_2}\). Então,
\[\delta_{1_2} = \varphi'(\nu_{1_2}) \sum\limits_{m=1}^{K_{saida}}(\delta_{m_{saida}} w_{1_2 m_{saida}}),\]
como em nosso exercício, \(K_{saida} = 1\), temos:
\[\delta_{1_2} = \varphi'(\nu_{1_2}) (\delta_{1_{saida}} w_{1_2 1_{saida}}).\]
Redes Neurais Artificiais - MLP
Exemplo
Logo,
\[\varphi'(\nu_{1_2}) = \dfrac{exp(-\nu_{1_2})}{(1 + exp(-\nu_{1_2}))^2} = \dfrac{exp(-1.8)}{(1 + exp(-1.8))^2} \approx 0.12,\]
assim,
\[\delta_{1_2} = 0.12*(0.13*0.61) \approx 0.01,\]
e portanto,
\[\dfrac{\partial E}{\partial w_{{1_1}{1_2}}} = 0.01*1 = 0.01,\]
assim,
\[w_{{1_1}{1_2}}(1) = w_{{1_1}{1_2}}(0) + \Delta w_{{1_1}{1_2}} = 0.8 - 0.8*(0.01) \approx 0.79.\]
Redes Neurais Artificiais - MLP
Exemplo
Agora, vamos ajustar o peso \(w_{{2_1}{1_2}}\), assim
\[\dfrac{\partial E}{\partial w_{{2_1}{1_2}}} = \delta_{1_2} x_2,\]
dos resultados anteriores, temos que \(x_2 = 1\) e \(\delta_{1_2} \approx 0.01\), logo
\[\dfrac{\partial E}{\partial w_{{2_1}{1_2}}} = 0.01*1 = 0.01,\]
porque o valor de \(x_2 = 1\). Assim,
\[w_{{2_1}{1_2}}(1) = w_{{2_1}{1_2}}(0) + \Delta w_{{2_1}{1_2}} = 0.3 - 0.8*(0.01) \approx 0.29.\]
Redes Neurais Artificiais - MLP
Exemplo
Agora vamos ajustar o peso \(w_{{1_1}{2_2}}\), que é dado por
\[\dfrac{\partial E}{\partial w_{{1_1}{2_2}}} = \delta_{2_2} x_1,\]
precisamos encontrar o valor de \(\delta_{2_2}\), que é dado por
\[\delta_{2_2} = \varphi'(\nu_{2_2}) (\delta_{1_{saida}} w_{2_2 1_{saida}})\]
então,
\[\delta_{2_2}= \dfrac{exp(-(-1.4))}{(1 + exp(-(-1.4)))^2} \left( 0.13*(-0.82) \right) \approx -0.02,\]
Redes Neurais Artificiais - MLP
Exemplo
Assim, temos que
\[\dfrac{\partial E}{\partial w_{{1_1}{2_2}}} = -0.02*1 = -0.02,\]
então, o valor do peso atualizado é
\[w_{{1_1}{2_2}}(1) = w_{{1_1}{2_2}}(0) + \Delta w_{{1_1}{2_2}} = -0.6 + 0.8*(0.02) \approx -0.58.\]
Redes Neurais Artificiais - MLP
Exemplo
Para atualizar o peso \(w_{{2_1}{2_2}}\), temos:
\[\dfrac{\partial E}{\partial w_{{2_1}{2_2}}} = \delta_{2_2} x_2,\]
assim,
\[\dfrac{\partial E}{\partial w_{{2_1}{2_2}}} = -0.02*1 = -0.02,\]
logo,
\[w_{{2_1}{2_2}}(1) = w_{{2_1}{2_2}}(0) + \Delta w_{{2_1}{2_2}} = -0.4 + 0.8*(0.02) \approx -0.38.\]
Redes Neurais Artificiais - MLP
Exemplo
Vamos agora atualizar os vieses \(b_{1_2}\) e \(b_{2_2}\). Para atualizar o viés \(b_{1_2}\), temos:
\[\dfrac{\partial E}{\partial b_{1_2}} = \delta_{1_2},\]
logo,
\[\dfrac{\partial E}{\partial b_{1_2}} = 0.01,\]
e assim,
\[b_{1_2}(1) = b_{1_2}(0) + \Delta b_{1_2} = 0.7 - 0.8*(0.01) \approx 0.69.\]
Redes Neurais Artificiais - MLP
Exemplo
Para atualizar o viés \(b_{2_2}\), temos:
\[\dfrac{\partial E}{\partial b_{2_2}} = \delta_{2_2},\]
logo,
\[\dfrac{\partial E}{\partial b_{2_2}} = -0.02,\]
e assim,
\[b_{2_2}(1) = b_{2_2}(0) + \Delta b_{2_2} = -0.4 + 0.8*(0.02) \approx -0.38.\]
Redes Neurais Artificiais - MLP
Exemplo
Com todos os valores atualizados, podemos fazer uma nova iteração \(t=1\) da rede.
Primeiramente, calculamos as ativações dos neurônios da camada oculta 2:
\(\nu_{1_2} = w_{{1_1}{1_2}}(1) x_1 + w_{{2_1}{1_2}}(1) x_2 + b_{1_2}(1) \approx 0.79*1 + 0.29*1 + 0.69 \approx 1.77\)
\(\nu_{2_2} = w_{{1_1}{2_2}}(1) x_1 + w_{{2_1}{2_2}}(1) x_2 + b_{2_2}(1) \approx -0.58*1 + -0.38*1 - 0.38 \approx -1.34\)
os resultados das funções de ativação são dadas por:
\(\varphi_{1_2}(\nu_{1_2}) = \dfrac{1}{1 + e^{-1.77}} \approx 0.85\)
\(\varphi_{2_2}(\nu_{2_2}) = \dfrac{1}{1 + e^{1.34}} \approx 0.21\)
Redes Neurais Artificiais - MLP
Exemplo
E assim,
\[\nu_{1_{saida}} = w_{{1_2}{1_{saida}}}(1) \varphi_{1_2}(\nu_{1_2}) + w_{{2_2}{1_{saida}}}(1) \varphi_{2_2}(\nu_{2_2}) + b_{1_{saida}}(1) \\ \quad\quad\, \approx 0.61*0.85 + (-0.82)*0.21 - 0.40 \approx -0.05\]
e
\[\hat{y} = \varphi_{1_{saida}}(\nu_{1_{saida}}) = \dfrac{1}{1 + e^{-(-0.05)}} \approx 0.49\]
Assim, temos que o erro nessa iteração foi \[e = y - \hat{y} = 0 - 0.49 = -0.49\]
Que foi menor que o erro da iteração anterior, que era \(-0.53\).
Referências para serem utilizadas
BRAGA, A. P.; CARVALHO, A.; LUDEMIR, T. Redes Neurais Artificiais: Teoria e Aplicações. .: [s.n.], 2000.
HOPFWELD, J. J. Neural networks and physical systems with emergent collective computational abilities. Proc. NatL Acad. Sci., v. 79, p. 2554–2558, 1982.
LUDWIG, O.; MONTGOMERY, E. Redes Neurais - Fundamentos e Aplicações com Programas em C. .: Ciência Moderna, 2007.
MINSKY, M.; PAPERT, S. Perceptrons: an introduction to computationational geometry. [S.l.]: MIT Press, 1969.
PINHEIRO, C. A. R. Inteligência Analítica: Mineração de Dados e Descoberta de Conhecimento. .: [s.n.], 2008.
RICH, E.; KNIGHT, K. Inteligência Artificial. .: [s.n.], 1993.
ROSENBLATT, F. Principles of Neurodynamics: Perceptrons and Theory of Brain Mechanisms. .: Washigton, DC, 1962.
https://acervolima.com/funcoes-de-ativacao/
OBRIGADO!
Slide produzido com quarto
Tópicos Especiais em Estatística Comp. - Prof. Jodavid Ferreira