Tópicos Especiais em Estatística Comp.
Avaliando a Acurácia do Modelo
UFPE
Avaliando a Acurácia do Modelo
Uma tarefa importante é entender como nossos métodos estatísticos estão performando em um conjunto de dados.
Selecionar a melhor abordagem pode ser uma das partes mais desafiadoras da aplicação do aprendizado estatístico na prática.
Discutiremos alguns dos conceitos mais importantes que surgem ao selecionar um procedimento de aprendizado estatístico para um conjunto de dados específico.
Abordaremos:
Medindo a Qualidade do Ajuste: Como avaliar o desempenho do modelo.
O Trade-Off Viés-Variância: Um conceito fundamental na seleção de modelos.
Medindo a Qualidade do Ajuste
Para avaliar o desempenho de um método de aprendizado estatístico em um determinado conjunto de dados, precisamos de alguma forma de medir quão bem suas predições correspondem aos dados observados.
Precisamos quantificar até que ponto o valor de resposta predito para uma determinada observação está próximo do valor de resposta verdadeiro para essa observação.
Erro Quadrático Médio (MSE)
No cenário de regressão, a medida mais comumente usada é o erro quadrático médio (MSE):
\[ \text{MSE} = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{f}(x_i))^2 \]
onde:
- \(y_i\) é o valor de resposta verdadeiro para a \(i\)-ésima observação.
- \(\hat{f}(x_i)\) é a previsão que nosso modelo \(\hat{f}\) fornece para a \(i\)-ésima observação. \(\hat{f}\) representa nossa função estimada.
- \(n\) é o número total de observações.
O MSE é a média das diferenças quadráticas entre os valores previstos e os reais.
Interpretando o MSE
- MSE Baixo: As respostas preditas estão, em média, muito próximas das respostas verdadeiras (bom ajuste). Quanto menor o MSE, menor o desvio típico das previsões em relação aos valores verdadeiros.
- MSE Alto: Para algumas observações, as respostas predistas e as verdadeiras diferem substancialmente (ajuste ruim). Um MSE maior indica discrepâncias médias maiores entre as previsões e os valores verdadeiros.
A Função de Risco:
Medindo o Desempenho
Como medimos o quão bem uma função de predição \(\hat{f}: \mathbb{R}^p \to \mathbb{R}\) se desempenha?
Precisamos de um critério. Em regressão, frequentemente usamos uma Função de Perda \(\mathcal{L}(predito, real)\) para quantificar o erro de uma única predição.
Exemplos:
- Perda Quadrática: \(\mathcal{L}(\hat{f}(X), Y) = (Y - \hat{f}(X))^2\)
- Perda Absoluta: \(\mathcal{L}(\hat{f}(X), Y) = |Y - \hat{f}(X)|\)
O Risco de uma função \(\hat{f}\) é sua perda esperada sobre os dados \((X, Y)\).
\[R(\hat{f}) = E[\mathcal{L}(\hat{f}(X), Y)]\]
A Função de Risco: (Perda Quadrática)
Usando a perda quadrática, a predição neste caso é chamada de Erro Quadrático Médio (MSE):
\[R(\hat{f}) = E[(Y - \hat{f}(X))^2]\]
- Aqui, \((X, Y)\) representa uma observação não conhecida.
- A esperança é calculada sobre a distribuição conjunta de \((X, Y)\).
Risco de Predição
e Estimação de Regressão
Seja \((X_{novo}, Y_{novo})\) uma nova observação não usada para estimar ou treinar \(\hat{f}\)
Usando a perda quadrática, o risco de predição neste caso é chamado de MSE de predição:
\[R_{pred}(\hat{f}) = E[(Y_{novo} - \hat{f}(X_{novo}))^2]\]
- Quanto menor o risco \(R_{pred}(\hat{f})\), melhor a função de predição \(\hat{f}\).
Risco de Predição
e Estimação de Regressão
Minimizar o risco de predição (com perda quadrática) \(R_{pred}(\hat{f})\) está intimamente relacionado à estimação da função de regressão \(f(x) = E[Y|X=x]\).
Vamos definir o risco de regressão como o MSE para estimar \(f(X)\):
\[R_{reg}(\hat{f}) = E \left[ \left(f(X) - \hat{f}(X) \right)^2\right]\]
O teorema a seguir formaliza essa conexão.
Risco de Predição
e Estimação de Regressão
Teorema 1: Suponha que definimos o risco de predição de \(\hat{f}: \mathbb{R}^p \to \mathbb{R}\) via perda quadrática: \(R_{pred}(\hat{f}) = E \left[ \left(Y - \hat{f}(X) \right)^2\right]\), onde \((X, Y)\) é uma nova observação. Seja o risco de regressão \(R_{reg}(\hat{f}) = E \left[ \left(f(X) - \hat{f}(X) \right)^2\right]\), onde \(f(X) = E[Y|X]\). Então:
\[R_{pred}(\hat{f}) = R_{reg}(\hat{f}) + E[Var[Y|X]]\]
1
Risco de Predição
e Estimação de Regressão
Prova.: \[ \begin{aligned} R_{pred}(\hat{f}) &= E\left[\left(Y - \hat{f}(X)\right)^2\right] \\ &= E\left[\left(Y - f(X) + f(X) - \hat{f}(X)\right)^2\right] \\ &= E\left[ \left(f(X) - \hat{f}(X)\right)^2 + \left(Y - f(X)\right)^2 + 2 \left(f(X) - \hat{f}(X) \right) \left(Y - f(X) \right) \right] \\ &= E\left[\left(f(X) - \hat{f}(X) \right)^2 \right] + E\left[\left(Y - f(X) \right)^2 \right] + 2 E\left[\left(f(X) - \hat{f}(X) \right) \left( Y - f(X) \right) \right] \end{aligned} \]
Risco de Predição
e Estimação de Regressão
Agora considere o termo cruzado, usando a Lei da Esperança Total1: \[E[A] = E[E[A|X]]\]
\[ \begin{aligned} E \left[ \left(f(X) - \hat{f}(X) \right) \left(Y - f(X) \right) \right] &= E\Big[ E \left[ \left( f(X) - \hat{f}(X) \right) \left( Y - f(X) \right) | X \right] \Big] \\ &= E\Big[ \left( f(X) - \hat{f}(X) \right) \underbrace{E \left[ \left( Y - f(X) \right) | X \right]}_{= E[Y|X] - f(X) = 0} \Big] \\ &= E \left[ \left( f(X) - \hat{f}(X) \right) \cdot 0 \right] = 0 \end{aligned} \]
Risco de Predição
e Estimação de Regressão
Então, o termo cruzado é zero. Ficamos com:
\[R_{pred}(\hat{f}) = E[(f(X) - \hat{f}(X))^2] + E[(Y - f(X))^2]\]
O primeiro termo é a definição do risco de regressão: \[E[(f(X) - \hat{f}(X))^2] = R_{reg}(\hat{f})\]
O segundo termo é a variância condicional esperada: \[E[(Y - f(X))^2] = E[ E[ (Y - f(X))^2 | X ] ] = E[Var[Y|X]]\]
Portanto: \[R_{pred}(\hat{f}) = R_{reg}(\hat{f}) + E[Var[Y|X]]\]
\(\square\)
Implicação do Teorema 1
\[R_{pred}(\hat{f}) = \underbrace{E \left[ \left( f(X) - \hat{f}(X) \right)^2 \right]}_{R_{reg}(\hat{f}) \text{ (Erro Redutível)}} + \underbrace{E \left[ Var[Y|X] \right]}_{\text{Erro Irredutível}}\]
- O termo \(E \left[Var[Y|X] \right]\) representa a variabilidade inerente de \(Y\) em torno de sua média \(f(X)\). Ele não depende da nossa escolha da função de predição \(\hat{f}\). Este é o menor erro de predição possível de se atingir, mesmo que conhecêssemos o verdadeiro \(f(x)\).
- Minimizar o risco de predição \(R_{pred}(\hat{f})\) é equivalente a minimizar o risco de regressão \(R_{reg}(\hat{f})\).
- A melhor função de predição possível sob perda quadrática é a verdadeira função de regressão \(\hat{f}(x) = f(x)\), pois isso torna \(R_{reg}(\hat{f}) = 0\).
\[\underset{\hat{f}}{\operatorname{arg min}} R_{pred}(\hat{f}) = \underset{\hat{f}}{\operatorname{arg min}} R_{reg}(\hat{f}) = f(x)\]
Interpretação Frequentista
Risco Condicional
Por que um baixo risco condicional \(R(\hat{f}) = E \left[\mathcal{L}(\hat{f}(X), Y) \right]\) é desejável?
Imagine que observamos um grande e novo conjunto de dados (de validação) \((X_{n+1}, Y_{n+1}), \dots, (X_{n+m}, Y_{n+m})\), amostrado i.i.d da mesma distribuição que \((X, Y)\).
Pela Lei dos Grandes Números, se \(m\) for grande, a perda média nestes novos dados se aproximará do risco:
\[ \frac{1}{m} \sum_{i=1}^{m} \mathcal{L}(\hat{f}(X_{n+i}), Y_{n+i}) \approx R(\hat{f}) \]
Portanto, se \(R(\hat{f})\) é pequeno, esperamos que \(\hat{f}(X_{novo}) \approx Y_{novo}\) em média para observações futuras. Isso é válido para qualquer função de perda \(\mathcal{L}\).
O Objetivo da Modelagem Preditiva
O objetivo dos métodos de um ponto de vista preditivo é, portanto:
Fornecer métodos que gerem bons estimadores \(\hat{f}\) da função verdadeira \(f(x)\), ou seja, estimadores com baixo risco \(R(\hat{f})\).
Na prática, não conhecemos \(f(x)\) e não podemos calcular \(R(\hat{f})\) exatamente, então precisamos de maneiras para estimar o risco ou escolher modelos que provavelmente terão baixo risco em dados não vistos1.
Overfitting, Underfitting e Bom Ajuste
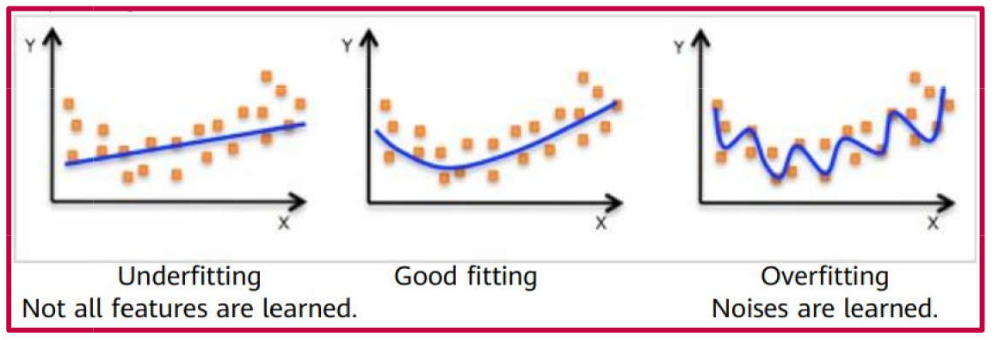
Overfitting
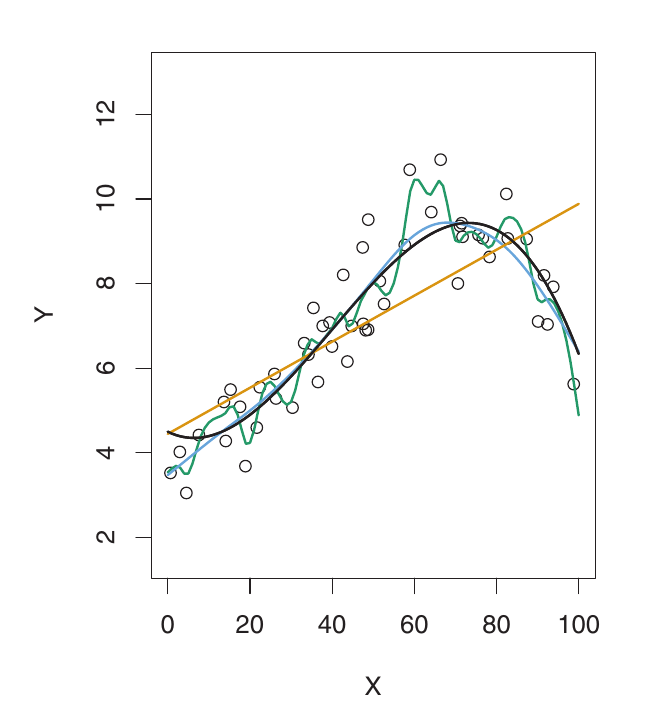
Esquerda: Dados simulados. A curva Preta é o f verdadeiro. Laranja: regressão linear. Azul & Verde: splines de suavização com diferentes flexibilidades.
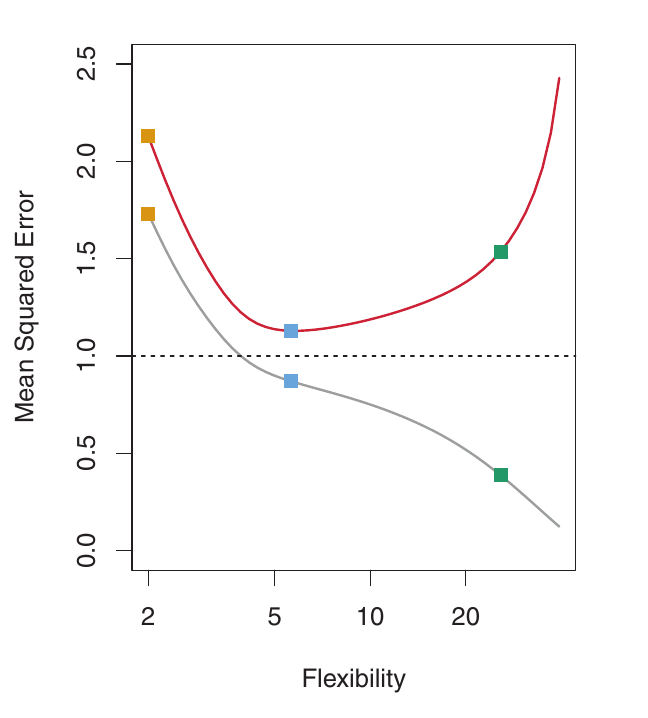
Direita: Cinza: MSE de Treino. Vermelho: MSE de Validação. Tracejado: Mínimo MSE de validação possível. Os quadrados mostram o MSE de treino/validação para os ajustes à esquerda.
Overfitting - Entendimento
- À medida que a flexibilidade aumenta, as curvas se ajustam mais de perto aos dados observados. O modelo é capaz de capturar relações mais complexas.
- A curva verde é a mais flexível – ela se ajusta muito bem aos dados de treino, mas é muito sinuosa e estima mal o verdadeiro f (curva preta). Isso é overfitting. O modelo está capturando ruído, não apenas o sinal subjacente.
- O MSE de treino (curva cinza) diminui monotonicamente à medida que a flexibilidade aumenta. Isso é sempre o caso – um modelo mais flexível sempre pode se ajustar melhor aos dados de treino. Isso é enganoso!
- O MSE de validação (curva vermelha) inicialmente diminui, e depois aumenta em forma de U. Este é o comportamento chave que queremos entender.
- A curva azul minimiza o MSE de validação – ela representa o melhor equilíbrio entre ajustar os dados de treino e generalizar para dados não vistos.
Overfitting - Um Problema Fundamental
- Quando um método produz um MSE de treino pequeno, mas um MSE de validação grande, estamos fazendo overfitting dos dados.
- O modelo está se esforçando demais para encontrar padrões nos dados de treino e pode estar captando padrões devido ao acaso (ruído) em vez de propriedades verdadeiras da função desconhecida f. Ele está memorizando os dados de treino em vez de aprender a relação geral.
- Overfitting significa que os padrões encontrados nos dados de treino não existem nos dados de validação, levando a um alto MSE de validação. O modelo generaliza mal.
- O MSE de treino é quase sempre menor que o MSE de validação, porque a maioria dos métodos minimiza direta ou indiretamente o MSE de treino.
- Overfitting se refere ao caso em que um modelo menos flexível produziria um MSE de Validação menor.
Underfitting
- O oposto de overfitting é underfitting.
- Um modelo sofre de underfitting quando não é flexível o suficiente para capturar a tendência subjacente nos dados.
- Isso resulta em alto viés. O modelo é muito simplista e perde padrões importantes. O modelo comete erros sistemáticos.
Underfitting
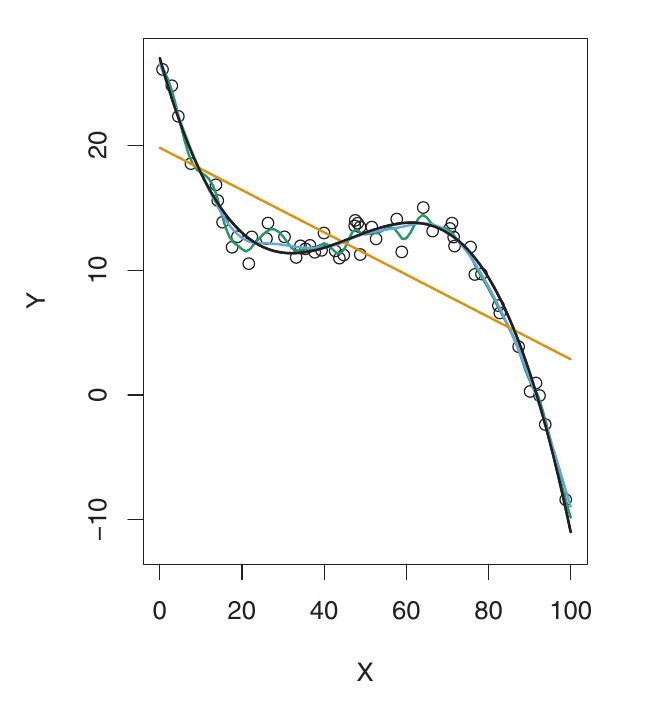
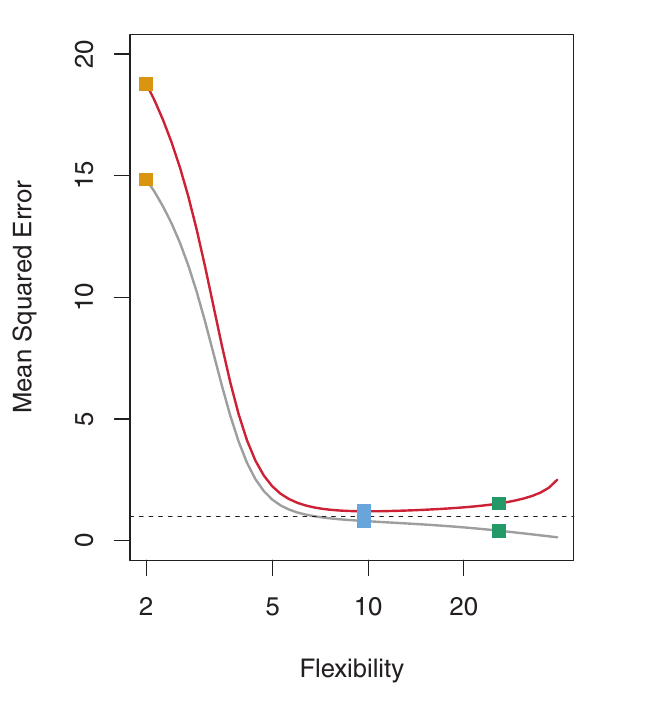
Aqui, f é altamente não linear. Tanto o MSE de treino quanto o de validação diminuem rapidamente antes que o MSE de validação comece a aumentar lentamente. É necessária mais flexibilidade do que no exemplo anterior. O modelo linear está sofrendo de underfitting.
Bom Ajuste
Exemplo: Dados Quase Lineares
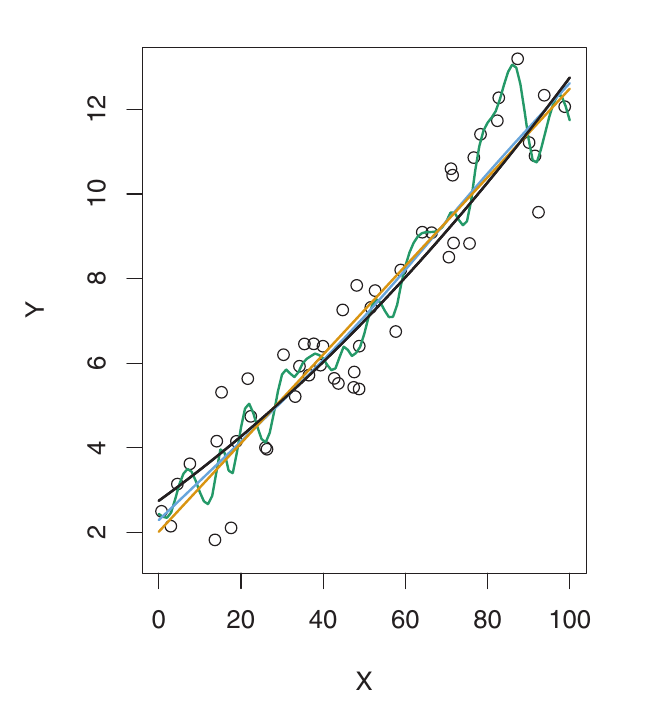
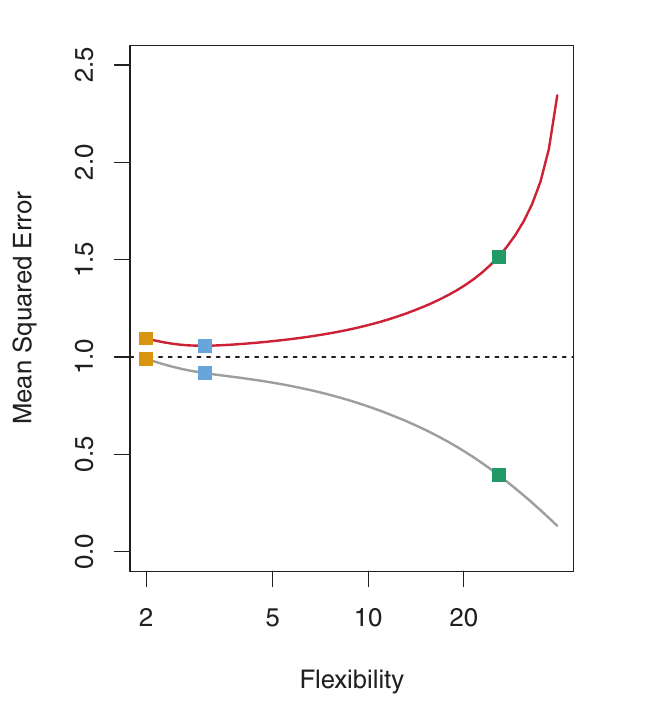
Aqui, o f verdadeiro é muito mais próximo do linear. A regressão linear fornece um bom ajuste. O MSE de validação diminui apenas ligeiramente antes de aumentar. O modelo linear simples tem o melhor desempenho. Os modelos mais flexíveis estão fazendo overfitting ao ruído.
Estimando o MSE de Validação na Prática
- Na prática, geralmente não temos um grande conjunto de validação designado prontamente disponível.
- O nível de flexibilidade correspondente ao MSE de validação mínimo varia consideravelmente entre os conjuntos de dados.
- Precisamos de métodos para estimar o MSE de validação usando os dados de treino disponíveis.
Duas abordagens comuns:
- Divisão de Dados (e Conjuntos de Validação)
- Validação Cruzada (Cross-Validation)
Estimando o MSE de Validação na Prática
- Na prática, geralmente não temos um grande conjunto de validação designado prontamente disponível.
- O nível de flexibilidade correspondente ao MSE de validação mínimo varia consideravelmente entre os conjuntos de dados.
- Precisamos de métodos para estimar o MSE de validação usando os dados de treino disponíveis.
Duas abordagens comuns:
Divisão de Dados (e Conjuntos de Validação)
- Validação Cruzada (Cross-Validation)
Divisão de Dados
Uma estratégia simples para estimar o erro de validação é a divisão de dados:
- Dividir aleatoriamente os dados disponíveis em duas partes:
- Conjunto de treino: Usado para ajustar (treinar) o modelo.
- Conjunto de validação: Usado para estimar o erro de validação. Não é usado para ajustar o modelo.
Ajustar o modelo usando o conjunto de treino. Isso significa estimar quaisquer parâmetros do modelo (por exemplo, coeficientes na regressão linear).
Prever as respostas para as observações no conjunto de validação usando o modelo ajustado.
Calcular o MSE (ou outra métrica de erro) no conjunto de validação. Isso fornece uma estimativa do MSE de validação.
Divisão de Dados
Suponha que tenhamos \(n\) observações: \((x_1, y_1), (x_2, y_2), ..., (x_n, y_n)\).
Podemos dividir os dados em:
- Conjunto de treino (ex: 70%): \((x_1, y_1), ..., (x_s, y_s)\)
- Conjunto de validação (ex: 30%): \((x_{s+1}, y_{s+1}), ..., (x_n, y_n)\)
Estimamos o risco, \(\hat{R}(f)\), que é uma aproximação do risco verdadeiro \(R(f)=E[\mathcal{L}(f(X);Y)]\), usando o conjunto de validação:
\[ \hat{R}(f) = \frac{1}{n-s} \sum_{i=s+1}^{n} (y_i - \hat{f}(x_i))^2 \]
onde \(\hat{f}\) é o modelo ajustado usando apenas os dados de treino, e a soma é sobre o conjunto de validação.
Divisão de Dados: Considerações
- Aleatorização: É crucial dividir os dados aleatoriamente. Uma divisão não aleatória pode levar a uma estimativa enviesada do erro de validação.
- Divisão Treino/Validação: A proporção de dados alocada para treino e validação pode variar (ex: 70/30, 80/20). Existe um trade-off:
- Mais dados no conjunto de treino geralmente levam a um melhor ajuste do modelo (menor viés).
- Mais dados no conjunto de validação geralmente levam a uma melhor estimativa do erro de validação (menor variância na estimativa).
O Trade-Off Viés-Variância
A forma de U observada nas curvas de MSE de validação (Figuras abaixo) é resultado de duas propriedades concorrentes dos métodos de aprendizado estatístico: viés e variância.



Impacto da Variância
Variância se refere à quantidade pela qual \(\hat{f}\) mudaria se a estimássemos usando um conjunto de dados de treino diferente.
Idealmente, a estimativa para f não deveria variar muito entre os conjuntos de treino. O modelo deve ser relativamente estável.
Alta variância: Pequenas mudanças nos dados de treino podem resultar em grandes mudanças em \(\hat{f}\). O modelo é muito sensível aos dados de treino específicos que vê.
Métodos estatísticos mais flexíveis geralmente têm maior variância. Eles podem se ajustar muito de perto aos dados de treino, mas isso pode levar a overfitting e alta variabilidade.
Impacto do Viés
Viés se refere ao erro introduzido ao aproximar um problema da vida real (que pode ser muito complexo) com um modelo mais simples.
- Exemplo: A regressão linear assume uma relação linear. Se a relação verdadeira estiver longe de ser linear, haverá viés. O modelo linear está sistematicamente errado.
- Métodos mais flexíveis geralmente resultam em menos viés. Eles podem capturar relações mais complexas nos dados.
O Trade-Off
- Regra geral: À medida que usamos métodos mais flexíveis, a variância aumenta e o viés diminui.
- A taxa relativa de mudança dessas duas quantidades determina se o MSE de validação aumenta ou diminui.
- Inicialmente, à medida que a flexibilidade aumenta, o viés diminui mais rápido do que a variância aumenta. Isso leva a uma diminuição no MSE de validação esperado.
- Em algum ponto, aumentar a flexibilidade tem pouco impacto no viés, mas aumenta significativamente a variância. É aqui que o overfitting começa. O MSE de validação esperado começa a aumentar.
Visualizando o Trade-Off
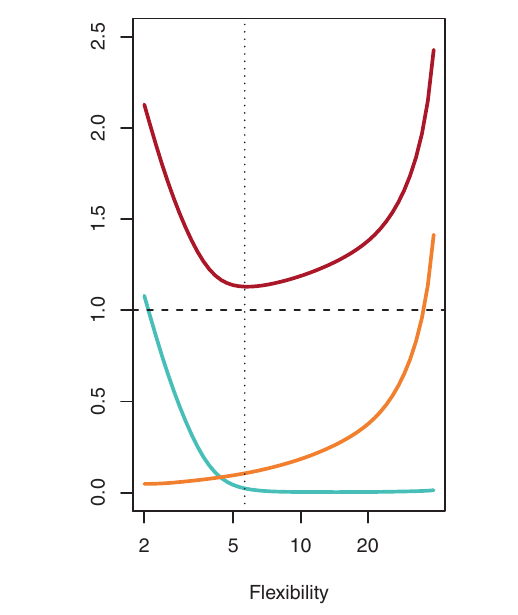
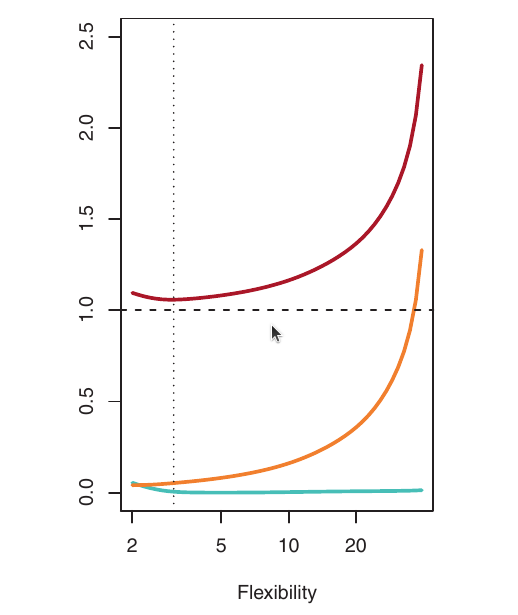
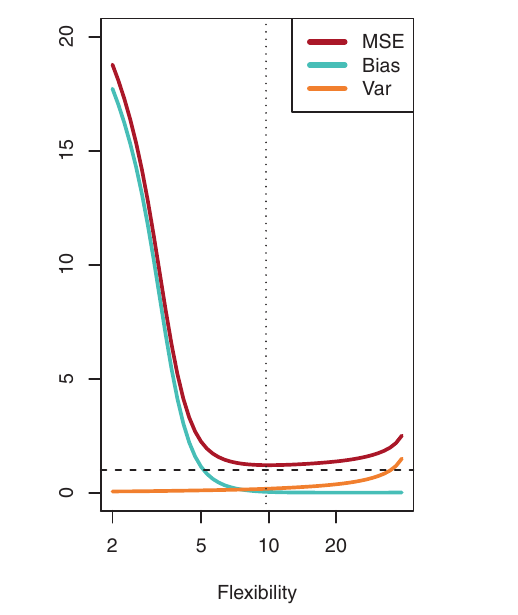
- Azul: Viés ao Quadrado
- Laranja: Variância
- Tracejado: Var(\(\epsilon\)) (erro irredutível)
- Vermelho: MSE de validação (soma dos anteriores)
O nível de flexibilidade ótimo (onde o MSE de validação é minimizado) difere entre os conjuntos de dados, dependendo do f verdadeiro e do nível de ruído.
Trade-Off Viés-Variância: Resumo
- Encontrar um bom modelo requer baixa variância e baixo viés.
- Isso é um trade-off porque é fácil obter:
- Baixo viés com alta variância: (ex: uma curva que interpola cada ponto de treino – altamente flexível, overfitting).
- Baixa variância com alto viés: (ex: uma linha horizontal – muito inflexível, underfitting).
- O desafio é encontrar um método com ambos, baixa variância e baixo viés. Isso requer a escolha do nível certo de complexidade do modelo.
Classificação
Taxa de Erro de Treino
Até agora, focamos em regressão (onde a variável resposta \(Y\) é quantitativa). Os conceitos de trade-off viés-variância também se aplicam à classificação (onde \(Y\) é qualitativa), com algumas modificações.
Em classificação, a medida mais comum de acurácia é a taxa de erro de treino:
\[ \frac{1}{n} \sum_{i=1}^{n} I(y_i \neq \hat{y}_i) \]
- \(\hat{y}_i\) é o rótulo de classe previsto para a \(i\)-ésima observação (usando nosso classificador ajustado).
- \(I(y_i \neq \hat{y}_i)\) é uma variável indicadora:
- \(I(y_i \neq \hat{y}_i) = 1\) se \(y_i \neq \hat{y}_i\) (classificação incorreta).
- \(I(y_i \neq \hat{y}_i) = 0\) se \(y_i = \hat{y}_i\) (classificação correta).
- Esta é a fração de classificações incorretas nos dados de treino.
Taxa de Erro de Validação
Como na regressão, estamos mais interessados na taxa de erro em observações de validação:
\[ \text{Ave}(I(\mathbf{y} \neq \mathbf{\hat{y}})) = \frac{1}{n_{\text{val}}} \sum_{i \in \mathcal{T}} I(y_i \neq \hat{y}_i) \]
\(\mathbf{\hat{y}}\) é o rótulo de classe previsto para uma observação de validação com o preditor \(\dot{\mathbf{x}}\).
Um bom classificador tem uma baixa taxa de erro de validação.
\(\mathcal{T}\) é o conjunto de índices das observações de validação.
Ave: abreviação de “Average” (Média)
Métricas de Desempenho
A Matriz de Confusão
- Uma tabela que resume o desempenho de um modelo de classificação.
- Compara os rótulos previstos com os rótulos reais (verdadeiros). Essencial para entender onde o modelo comete erros.
Estrutura (para um problema de classificação binária):
| Previsto: Positivo | Previsto: Negativo | Total Real | |
|---|---|---|---|
| Real: Positivo | TP | FN | TP + FN |
| Real: Negativo | FP | TN | FP + TN |
| Total Previsto | TP + FP | FN + TN | n |
A Matriz de Confusão
| Previsto: Positivo | Previsto: Negativo | Total Real | |
|---|---|---|---|
| Real: Positivo | TP | FN | TP + FN |
| Real: Negativo | FP | TN | FP + TN |
| Total Previsto | TP + FP | FN + TN | n |
- TP (True Positive / Verdadeiro Positivo): Instâncias positivas corretamente previstas (ex: fraude corretamente identificada).
- TN (True Negative / Verdadeiro Negativo): Instâncias negativas corretamente previstas (ex: não-fraude corretamente identificada).
- FP (False Positive / Falso Positivo / Erro Tipo I): Positivo incorretamente previsto (ex: não-fraude sinalizada como fraude).
- FN (False Negative / Falso Negativo / Erro Tipo II): Negativo incorretamente previsto (ex: fraude não detectada).
Matriz de Confusão
Exemplo de Cálculo
Cenário: Conjunto de validação (\(n=100\)), 10 Reais Positivos (Minoria), 90 Reais Negativos (Maioria).
Previsões do Modelo:
- Identifica corretamente 7 casos Positivos (TP = 7).
- Não detecta 3 casos Positivos (prevê como Negativos) (FN = 3).
- Sinaliza incorretamente 2 casos Negativos como Positivos (FP = 2).
- Identifica corretamente 88 casos Negativos (TN = 88).
Matriz de Confusão
Exemplo de Cálculo
Matriz de Confusão:
| Previsto: Positivo | Previsto: Negativo | Total Real | |
|---|---|---|---|
| Real: Positivo | 7 | 3 | 10 |
| Real: Negativo | 2 | 88 | 90 |
| Total Previsto | 9 | 91 | 100 |
- Verificação:
- TP+FN = 7+3=10 (Reais Pos);
- FP+TN = 2+88=90 (Reais Neg);
- Total = 100.
Matriz de Confusão
Exemplo de Cálculo
Matriz de Confusão:
| Previsto: Positivo | Previsto: Negativo | Total Real | |
|---|---|---|---|
| Real: Positivo | 7 | 3 | 10 |
| Real: Negativo | 2 | 88 | 90 |
| Total Previsto | 9 | 91 | 100 |
Qual é a acurácia e qual o seu valor?
- Acurácia: \(\frac{TP + TN}{n} = \frac{7 + 88}{100} = 95\%\)
Alta, certo?! Mas vamos olhar mais a fundo.
Precisão (Precision)
- Pergunta: De todas as instâncias que o modelo previu como Positivas, quantas eram realmente Positivas?
Fórmula: \[Precisão = \frac{TP}{TP + FP}\]
Foco: Minimizar Falsos Positivos (FP). Alta precisão significa que o modelo é confiável quando prevê a classe positiva.
Relevância: Importante quando o custo de um Falso Positivo é alto (ex: sinalizar uma transação legítima como fraude, enviar alertas desnecessários).
Precisão (Precision)
\[Precisão = \frac{TP}{TP + FP}\]
Usando o Exemplo:
TP = 7
FP = 2
Positivos Previstos = TP + FP = 7 + 2 = 9
Precisão: \(\frac{7}{7 + 2} = \frac{7}{9} \approx 0.778\) ou 77.8%
Interpretação: Quando este modelo prevê “Positivo”, ele está correto em cerca de 77.8% das vezes.
Recall
(Revocação / Sensibilidade / Taxa de Verdadeiros Positivos - TPR)
- Pergunta: De todas as instâncias reais Positivas, quantas o modelo identificou corretamente?
- Fórmula: \[Recall = \frac{TP}{TP + FN}\]
- Foco: Minimizar Falsos Negativos (FN). Alto recall significa que o modelo é bom em encontrar as instâncias positivas.
- Relevância: Crucial para dados desbalanceados onde a classe minoritária é importante. Essencial quando o custo de um Falso Negativo é alto (ex: não detectar uma transação fraudulenta, falhar em diagnosticar uma doença).
Recall
(Revocação / Sensibilidade / Taxa de Verdadeiros Positivos - TPR)
\[Recall = \frac{TP}{TP + FN}\]
Usando o Exemplo:
TP = 7
FN = 3
Positivos Reais = TP + FN = 7 + 3 = 10
Recall: \(\frac{7}{7 + 3} = \frac{7}{10} = 0.70\) ou 70.0%
Interpretação: Este modelo encontrou apenas 70% dos casos Positivos reais. 30% foram perdidos (FN). Isso destaca a fraqueza do modelo, ao contrário da acurácia de 95%.
\(F_1\)-Score
- Pergunta: Como podemos combinar Precisão e Recall em uma única métrica?
Fórmula: \[F_1 = 2 \times \frac{Precisão \times Recall}{Precisão + Recall}\]
Conceito: A média harmônica de Precisão e Recall. Ela dá mais peso a valores mais baixos, o que significa que penaliza mais modelos onde uma métrica é alta e a outra é muito baixa do que uma média simples faria.
Relevância: Útil quando você precisa de um equilíbrio entre Precisão e Recall, e não há uma razão forte para priorizar uma significativamente sobre a outra.
\(F_1\)-Score
\[F_1 = 2 \times \frac{Precisão \times Recall}{Precisão + Recall}\]
Usando o Exemplo:
Precisão ≈ 0.778
Recall = 0.70
\(F_1\)-Score: \(2 \times \frac{0.778 \times 0.70}{0.778 + 0.70} = 2 \times \frac{0.5446}{1.478} \approx 2 \times 0.368 \approx 0.737\)
Interpretação: O \(F_1\)-Score de 0.737 fornece uma visão mais equilibrada do desempenho do que a acurácia de 95%, refletindo o trade-off entre a precisão do modelo e sua capacidade de encontrar casos positivos.
MCC
Coeficiente de Correlação de Matthews
- Conceito: Um coeficiente de correlação entre as classificações binárias observadas e previstas. Mede a qualidade da classificação, considerando todos os quatro valores da matriz de confusão (TP, TN, FP, FN).
- Fórmula: \[MCC = \frac{TP \times TN - FP \times FN}{\sqrt{(TP + FP)(TP + FN)(TN + FP)(TN + FN)}}\]
- Intervalo: -1 a +1.
- +1: Predição perfeita.
- 0: Não é melhor que uma predição aleatória.
- -1: Discordância total entre a predição e a observação.
- Vantagens: Considerada uma das métricas mais robustas e balanceadas para conjuntos de dados desbalanceados. Ela produz uma pontuação alta apenas se o classificador tiver um bom desempenho tanto na classe minoritária quanto na majoritária. Menos influenciada pela distribuição de classes assimétrica em comparação com a Acurácia ou o F1-Score em alguns casos extremos.
MCC
Coeficiente de Correlação de Matthews
\[MCC = \frac{TP \times TN - FP \times FN}{\sqrt{(TP + FP)(TP + FN)(TN + FP)(TN + FN)}}\]
Usando o Exemplo:
- TP = 7, TN = 88, FP = 2, FN = 3
- Numerador: \((7 \times 88) - (2 \times 3) = 616 - 6 = 610\)
- Termos do Denominador:
- (TP + FP) = 7 + 2 = 9
- (TP + FN) = 7 + 3 = 10
- (TN + FP) = 88 + 2 = 90
- (TN + FN) = 88 + 3 = 91
- Denominador = \(\sqrt{9 \times 10 \times 90 \times 91} = \sqrt{737100} \approx 858.54\)
- MCC: \(\frac{610}{858.54} \approx 0.710\)
Interpretação: O valor do MCC de 0,71 indica uma correlação razoavelmente boa entre as previsões do modelo e as classes reais, levando em conta tanto as previsões corretas quanto as incorretas para ambas as classes de forma equilibrada.
Coeficiente Kappa de Cohen (\(\kappa\))
- Conceito: Mede a concordância entre as classificações previstas e as classificações reais, corrigindo para a concordância que poderia ocorrer puramente por acaso.
- Pergunta: O quão melhor é a concordância do classificador do que a concordância esperada por acaso?
- Intervalo: Tipicamente de -1 a +1, embora valores negativos abaixo de 0 sejam raros na prática.
- κ = 1: Concordância perfeita.
- κ = 0: Concordância equivalente ao acaso.
- κ < 0: Concordância mais fraca que o acaso (incomum).
- Diretrizes Gerais de Interpretação (Landis & Koch): <0 Pobre, 0-0.2 Leve, 0.21-0.4 Razoável, 0.41-0.6 Moderada, 0.61-0.8 Substancial, 0.81-1 Quase Perfeita.
- Fórmula: \[κ = \frac{P_o - P_e}{1 - P_e}\]
- \(P_o\) = Acurácia Observada = \(\frac{TP + TN}{n}\)
- \(P_{e}\,=\,{N^{-2}}{\sum_{i\,=\,1}^{c} n_{i+}\, n_{+i}}\),
\(n_{ii}\) é a soma de elementos na diagonal principal da matriz de confusão, \(n_{i+}\) é a soma dos elementos na \(i\)-ésima linha, \(n_{+i}\) é a soma dos elementos na \(i\)-ésima coluna, e \(N\) representa o número total de observações, ou seja, o número total de instâncias classificadas.
Coeficiente Kappa de Cohen (\(\kappa\))
\[κ = \frac{P_o - P_e}{1 - P_e}\]
Usando o Exemplo do Slide 42 (TP=7, TN=88, FP=2, FN=3, n=100):
- Acurácia Observada (\(P_o\)): \(\frac{7 + 88}{100} = 0.95\)
- Acurácia Esperada (\(P_e\)):
- \(P_e = 0.781\)
- Kappa (\(\kappa\)): \(\frac{0.95 - 0.781}{1 - 0.781} = \frac{0.169}{0.219} \approx 0.772\)
Interpretação: O valor Kappa de ~0.71 indica uma concordância substancial entre as previsões do modelo e os valores reais. Essa métrica reforça que o modelo aprendeu padrões.
Coeficiente Kappa de Cohen (\(\kappa\))
Classificação Multiclasse
\[ \kappa\,=\,\frac{P_{o}\,-\,P_{e}}{1\,-\,P_{e}}, \]
em que
\(P_{o}\,=\,{N}^{-1}{\sum_{i\,=\,1}^{c} n_{ii}}\),
\(P_{e}\,=\,{N^{-2}}{\sum_{i\,=\,1}^{c} n_{i+}\, n_{+i}}\),
\(n_{ii}\) é a soma de elementos na diagonal principal da matriz de confusão, \(n_{i+}\) é a soma dos elementos na \(i\)-ésima linha, \(n_{+i}\) é a soma dos elementos na \(i\)-ésima coluna, e \(N\) representa o número total de observações, ou seja, o número total de instâncias classificadas.
Coeficiente Kappa de Cohen (\(\kappa\))
Exemplo
Consideremos a seguinte Matriz de Classificação:
| Predito 1 | Predito 2 | Predito 3 | Total Verdadeiro | |
|---|---|---|---|---|
| Verdadeiro 1 | 50 | 10 | 5 | 65 |
| Verdadeiro 2 | 15 | 80 | 5 | 100 |
| Verdadeiro 3 | 10 | 5 | 70 | 85 |
| Total Predito | 75 | 95 | 80 | 250 |
Aqui, o total de observações é 250.
Cálculo dos Componentes do Kappa
Concordância Observada (\(P_o\))
Concordância Esperada (\(P_e\))
Coeficiente Kappa de Cohen (\(\kappa\))
Multiclasse
1. Cálculo de \(P_o\) (Concordância Observada)
A fórmula para \(P_o\) é: \(P_{o}\,=\,{N}^{-1}{\sum_{i\,=\,1}^{c} n_{ii}}\)
Aqui, \(n_{ii}\) são os elementos da diagonal principal da matriz de confusão.
Primeiro, calculamos a soma dos elementos na diagonal principal: \[ \sum_{i\,=\,1}^{c} n_{ii} = n_{11} + n_{22} + n_{33} = 50 + 80 + 70 = 200 \]
Agora, calculamos \(P_o\): \[ P_{o}\,=\,{N}^{-1} \times 200 = \frac{1}{250} \times 200 = \frac{200}{250} = 0.8 \]
Coeficiente Kappa de Cohen (\(\kappa\))
Multiclasse
2. Cálculo de \(P_e\) (Concordância Esperada por Acaso)
A fórmula para \(P_e\) é: \(P_{e}\,=\,{N^{-2}}{\sum_{i\,=\,1}^{c} n_{i+}\, n_{+i}}\)
Aqui, \(n_{i+}n_{+i}\) é o resultado da multiplicação da \(i\)-ésima linha com a \(i\)-ésima coluna.
Vamos listar os casos:
- \(n_{1+}n_{+1} = [50 \quad 10 \quad 5] [50 \quad 15 \quad 10]^\top = 2700\)
- \(n_{2+}n_{+1} = [15 \quad 80 \quad 5][10 \quad 80 \quad 5]^\top = 6575\)
- \(n_{3+}n_{+3} = [10 \quad 5 \quad 70][5 \quad 5 \quad 70] = 5200\)
Agora, calculamos \(P_e\): \[ P_{e}\,=\,{N^{-2}} \times 2700+6575+5200 = \frac{1}{250^2} \times 14475 = \frac{14475}{62500} = 0.2316 \]
Coeficiente Kappa de Cohen (\(\kappa\))
Multiclasse
Coeficiente \(\kappa\)
O coeficiente \(\kappa\) é então calculado usando a fórmula:
\[\kappa\,=\,\frac{P_{o}\,-\,P_{e}}{1\,-\,P_{e}}\]
\(\kappa = (0.8 - 0.2316) / (1 - 0.2316)\)
\(\kappa = 0.5684 / 0.7684\)
\(\kappa ≈ 0.7397\)
Isso indica uma concordância substancial entre as classificações, superior ao que seria esperado pelo acaso.
Qual Métrica Usar?
- Acurácia: Geralmente evite como a métrica principal para dados desbalanceados. Use apenas se as classes forem balanceadas ou os custos dos erros forem iguais (raro).
- Precisão: Priorize quando o custo de Falsos Positivos for alto.
- Recall (Sensibilidade/TPR): Priorize quando o custo de Falsos Negativos for alto (frequentemente o caso para classes minoritárias como fraude/doença).
- \(F_1\)-Score: Use quando precisar de um equilíbrio entre Precisão e Recall.
- MCC (Coeficiente de Correlação de Matthews): Uma métrica robusta que considera todas as quatro entradas da matriz de confusão (TP, TN, FP, FN). Bom resumo em um único número, menos sensível à assimetria de classes do que o F1 em alguns casos.
- Kappa (κ de Cohen): Mede a concordância em relação ao que é esperado por acaso. Útil em cenários desbalanceados, pois leva em conta explicitamente a possibilidade de alta “concordância por acaso” devido a uma grande classe majoritária.
Recomendação: Sempre olhe primeiro para a Matriz de Confusão.
Referências
Básicas
Aprendizado de Máquina: uma abordagem estatística, Izibicki, R. and Santos, T. M., 2020, link: https://rafaelizbicki.com/AME.pdf.
An Introduction to Statistical Learning: with Applications in R, James, G., Witten, D., Hastie, T. and Tibshirani, R., Springer, 2013, link: https://www.statlearning.com/.
Mathematics for Machine Learning, Deisenroth, M. P., Faisal. A. F., Ong, C. S., Cambridge University Press, 2020, link: https://mml-book.com.
Referências
Complementares
An Introduction to Statistical Learning: with Applications in python, James, G., Witten, D., Hastie, T. and Tibshirani, R., Taylor, J., Springer, 2023, link: https://www.statlearning.com/.
Matrix Calculus (for Machine Learning and Beyond), Paige Bright, Alan Edelman, Steven G. Johnson, 2025, link: https://arxiv.org/abs/2501.14787.
Machine Learning Beyond Point Predictions: Uncertainty Quantification, Izibicki, R., 2025, link: https://rafaelizbicki.com/UQ4ML.pdf.
Mathematics of Machine Learning, Petersen, P. C., 2022, link: http://www.pc-petersen.eu/ML_Lecture.pdf.
Tópicos Especiais em Estatística Comp. - Prof. Jodavid Ferreira