Para motivar nosso estudo de aprendizado estatístico, vamos iniciar com um exemplo:
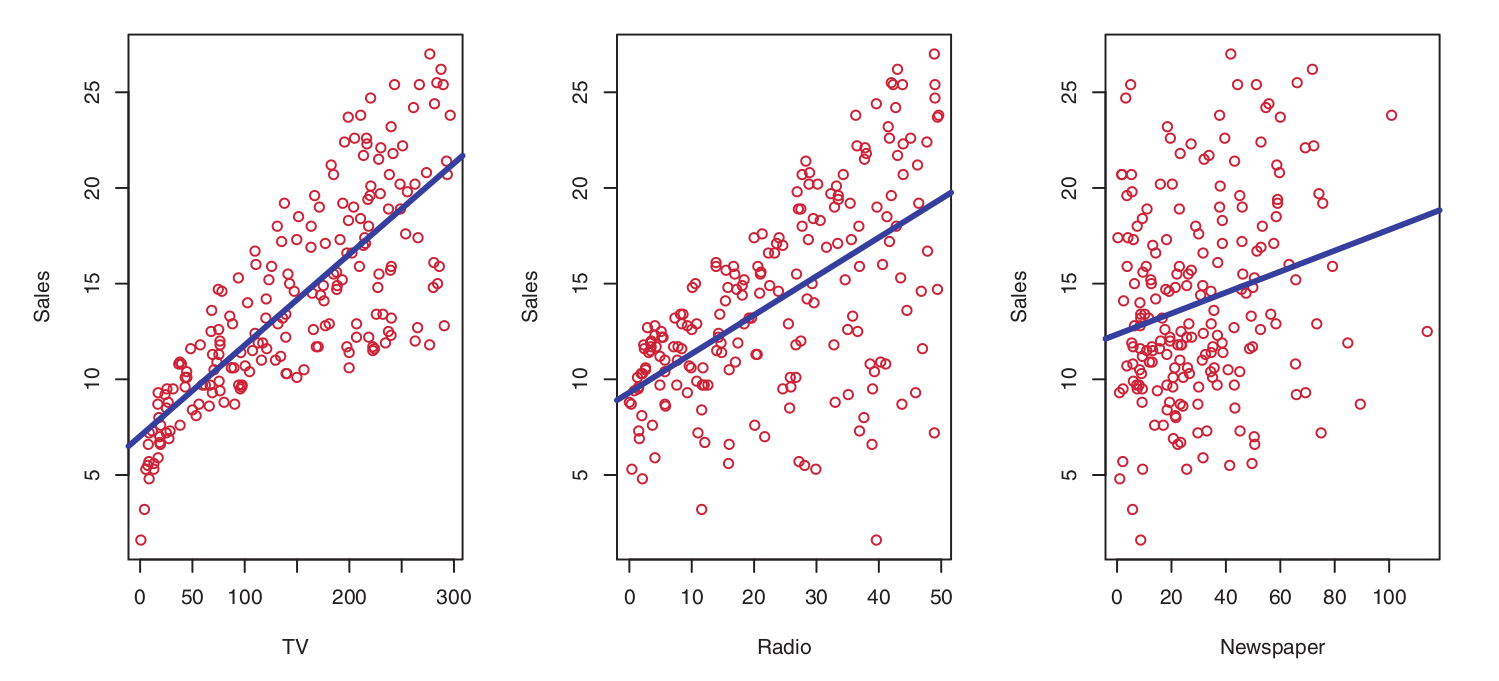
Suponha que sejamos consultores estatísticos contratados por um cliente para fornecer orientações sobre como melhorar as vendas de um determinado produto.
O conjunto de dados Advertising consiste nas vendas desse produto em 200 diferentes mercados, juntamente com os orçamentos de publicidade para o produto em cada um desses mercados, considerando três diferentes mídias: TV, rádio e jornal.
Nosso cliente não pode aumentar diretamente as vendas do produto. No entanto, ele pode controlar os gastos com publicidade em cada uma das três mídias.
Portanto, se determinarmos que existe uma associação entre publicidade e vendas, podemos instruir o cliente a ajustar os orçamentos de publicidade, aumentando indiretamente as vendas. Em outras palavras, nosso objetivo é desenvolver um modelo preciso que possa ser utilizado para prever as vendas com base nos orçamentos das três mídias.
Aprendizagem Estatística?
Para motivar nosso estudo de aprendizado estatístico, vamos iniciar com um exemplo:
Nesse contexto, os orçamentos de publicidade são as variáveis de entrada, enquanto as vendas é a variável de saída.
As variáveis de entrada são geralmente representadas pelo símbolo \(X\), com um subscrito para diferenciá-las. Assim,
\(X_1\) pode representar o orçamento para TV
\(X_2\) o orçamento para rádio e
\(X_3\) o orçamento para jornal.
As variáveis de entrada podem receber diferentes nomes, como preditoras, variáveis independentes, features ou, às vezes, apenas variáveis.
Já a variável de saída, que neste caso são as vendas, é frequentemente chamada de resposta, variável dependente, label e é geralmente representada pelo símbolo \(Y\).
Aprendizagem Estatística?
Aprendizagem Estatística?
Exemplo 2:
Isomap face data
Dado um conjunto de dados de faces, o objetivo é indicar a direção para a qual uma pessoa está olhando, com base em uma imagem desta pessoa.
Uma forma de fazer isso é criar um modelo que utilize as imagens de faces como variáveis de entrada e traga como resposta a direção da face. Assim,
\(X_1\) imagem da face
e
\(Y\) direção da face
Aprendizagem Estatística?
De forma mais geral, suponha que desejamos observar uma resposta quantitativa \(Y \in \mathbb{R}\) e \(p\) preditores diferentes, \(X_1, X_2, \dots, X_p \in \mathbb{R}\).
Assumimos que existe alguma relação entre \(Y\) e \(\mathbf{x} = (X_1, X_2, \dots, X_p)\), que pode ser escrita de forma bastante geral como:
\[
Y = f(\mathbf{x}) + \varepsilon,
\]
em que \(\mathbf{x} \in \mathbb{R}^p\), \(f(\cdot)\) é uma função única, porém desconhecida, de \(X_1, \dots, X_p\), e \(\varepsilon\) é um termo de erro aleatório, que é independente de \(\mathbf{x}\) e possui média zero, ou seja, \(E(\varepsilon) = 0\).
Nesta formulação, \(f(\cdot)\) é a função que representa a informação sistemática que \(\mathbf{x}\) fornece sobre \(Y\).
Aprendizagem Estatística?
A aprendizagem estatística refere-se a um conjunto de abordagens para estimar \(f(\cdot)\), ou seja, encontrar \(\hat{f}(\cdot)\) que mais se aproxime de \(f(\cdot)\)
Criar novos algoritmos, novas abordages, novos modelos a partir dos algoritmos, bem como avaliar as estimativas obtidas por tais modelos, é o foco da Aprendizagem Estatística e Aprendizagem de Máquina.
Por que estimar \(f(\cdot)\)?
Existem duas razões principais pelas quais podemos desejar estimar \(f(\cdot)\):
Inferência e
Predição
As Duas Culturas
Breiman1 argumenta que existem duas abordagens no uso de modelos estatísticos, especialmente em regressão.
De maneira geral, a primeira abordagem, denominada por Breiman, é a predominante na comunidade estatística. Nessa perspectiva, assume-se que o modelo adotado para \(f(\cdot)\), ou seja, \(g = \hat{f} : \mathbb{R}^p \to \mathbb{R}\)
sendo \(\dot{\mathbf{x}}_i = [x_{i1}, \ldots, x_{ij} ]^\top\) a \(i\)-ésima observação da \(j\)-variável, é corretamente especificado. Isso, porque o principal interesse reside na interpretação dos parâmetros do modelo (nesse caso, os \(\beta_i\)’s);
em particular, há um foco na realização de testes de hipóteses e na construção de intervalos de confiança para esses parâmetros.
Dentro dessa abordagem, a verificação das suposições do modelo, como normalidade dos erros, linearidade e homocedasticidade, é considerada essencial. Embora a predição possa ser um dos objetivos, a ênfase principal recai sobre a inferência estatística.
As Duas Culturas
Inferência
Muitas vezes, estamos interessados em entender como \(Y\) é afetado à medida que \(X_1, \ldots, X_p\) mudam.
Nessa situação, desejamos estimar \(f\), mas nosso objetivo não é necessariamente fazer predições para \(Y\).
Em vez disso, queremos entender a relação entre \(\mathbf{x}\) e \(Y\), ou mais especificamente, entender como \(Y\) muda em função dos \(X_1, \ldots, X_p\).
Nesse caso, \(g = \hat{f}\) não pode ser tratada como uma “caixa preta”, porque precisamos entender a sua forma exata.
As Duas Culturas
Inferência
Nesse contexto, pode-se estar interessado em responder às seguintes perguntas:
Quais preditores estão associados à resposta?
Muitas vezes, apenas uma pequena fração dos preditores disponíveis está substancialmente associada a \(Y\). Identificar os poucos preditores importantes dentre um grande conjunto de variáveis possíveis pode ser extremamente útil, dependendo da aplicação.
Qual é a relação entre a resposta e cada preditor?
Alguns preditores podem ter uma relação positiva com \(Y\), no sentido de que o aumento do preditor está associado ao aumento dos valores de \(Y\). Outros preditores podem ter a relação oposta. Dependendo da complexidade de \(f\), a relação entre a resposta e um determinado preditor também pode depender dos valores dos outros preditores.
As Duas Culturas
Inferência
A relação entre \(Y\) e cada preditor pode ser adequadamente resumida por uma equação linear, ou essa relação é mais complicada?
Historicamente, a maioria dos métodos para estimar \(f\) assumiu uma forma linear. Em algumas situações, essa suposição é razoável ou até mesmo desejável. Mas, frequentemente, a verdadeira relação é mais complexa, caso em que um modelo linear pode não fornecer uma representação precisa da relação entre as variáveis de entrada e saída.
As Duas Culturas
Inferência
Considere os dados de publicidade ilustrados na abaixo:
Pode-se estar interessado em responder a perguntas como:
Quais mídias contribuem para as vendas?
Quais mídias geram o maior aumento nas vendas? ou
Quanto aumento nas vendas está associado a um determinado aumento na publicidade na TV?
Essa situação se enquadra no paradigma de inferência.
As Duas Culturas
A segunda abordagem, denominada algorithmic modeling culture, é a que domina a comunidade de Aprendizado de máquina (machine learning).
Aqui, temos o interesse de responder o seguinte questionamento:
Como podemos criar uma função \(g = \hat{f} : \mathbb{R}^p \to \mathbb{R}\) que tenha bom poder preditivo?
Como criar \(g\) tal que, dadas novas observações i.i.d. \((\dot{\mathbf{x}}_{i+1}, \dots, \dot{\mathbf{x}}_{i+h})\), sendo \(i,h\) quantidades de observações, tenhamos
O principal objetivo neste caso é a predição de novas observações
Diferentemente da abordagem anterior, não se assume que o modelo representa perfeitamente a realidade subjacente; em vez disso, ele é desenvolvido com o objetivo de capturar padrões e dinâmicas dos dados observados.
Em geral, não há nenhum modelo probabilístico explícito por trás dos algoritmos utilizados.
Mesmo que o principal objetivo de um modelo computacional seja a reprodução fiel dos fenômenos estudados, alguas vezes a interpretabilidade do modelo torna-se fundamental para a validação dos resultados e para a extração de conhecimento a partir das predições.
As Duas Culturas
Predição
Em muitas situações, um conjunto de entradas \(\dot{\mathbf{x}}\) está prontamente disponível, mas a saída \(Y\) não pode ser facilmente obtida. Nesse contexto, como o termo de erro tem média zero, podemos prever \(Y\) usando
onde \(g\) representa nossa estimativa para \(f\), e \(\hat{Y}\) representa o estimador para a predição de um \(y\) resultante para \(Y\).
Nesse cenário, \(g\) é frequentemente tratada como uma “caixa preta”, no sentido de que não estamos tipicamente preocupados com a forma exata de \(g\), desde que ela forneça predições precisas para \(Y\).
As Duas Culturas
Predição
A precisão de \(y\) como uma predição para \(Y\) depende de duas quantidades, que chamaremos de erro redutível e erro irredutível.
Em geral, \(g = \hat{f}\) não será uma estimativa perfeita para \(f\), e essa imprecisão introduzirá algum erro.
Esse erro é redutível porque podemos potencialmente melhorar a precisão de \(g\) usando a técnica de aprendizagem estatística mais adequada para estimar \(f\).
Entretanto, mesmo que fosse possível obter uma estimativa perfeita para \(f\), \(Y\) é também uma função de \(\epsilon\), que, por definição, não pode ser predita usando \(\dot{\mathbf{x}}\).
Portanto, a variabilidade associada a \(\epsilon\) também afeta a precisão de nossas predições. Esse é o chamado erro irredutível, porque, não importa quão bem estimemos \(f\), não podemos reduzir o erro introduzido por \(\epsilon\).
As Duas Culturas
Predição
Exemplo:
O risco de uma reação adversa pode variar para um determinado paciente em um determinado dia, dependendo de variações na fabricação do medicamento ou do estado geral de bem-estar do paciente naquele dia, ou seja, não temos controle sobre a variações na fabricação do medicamento e sobre o bem-estar do paciente em cada dia.
As Duas Culturas
Predição
Considere a função \(g\) como uma estimativa para \(f\), e um conjunto de preditores \(\dot{\mathbf{x}}\), que resulta na predição \(\hat{Y} = g(\dot{\mathbf{x}})\). Suponha por um momento que tanto \(g\) quanto \(\dot{\mathbf{x}}\) são fixos. Então, temos que
onde \(E(Y - \hat{Y})^2\) representa o valor esperado da diferença quadrada entre o valor predito e o valor real de \(Y\), e \(\text{Var}(\epsilon) = E[\epsilon^2] - \left[ E(\epsilon) \right]^2\) representa a variância associada ao termo de erro \(\epsilon\), e \(E(\epsilon) = 0\).
As Duas Culturas
Predição
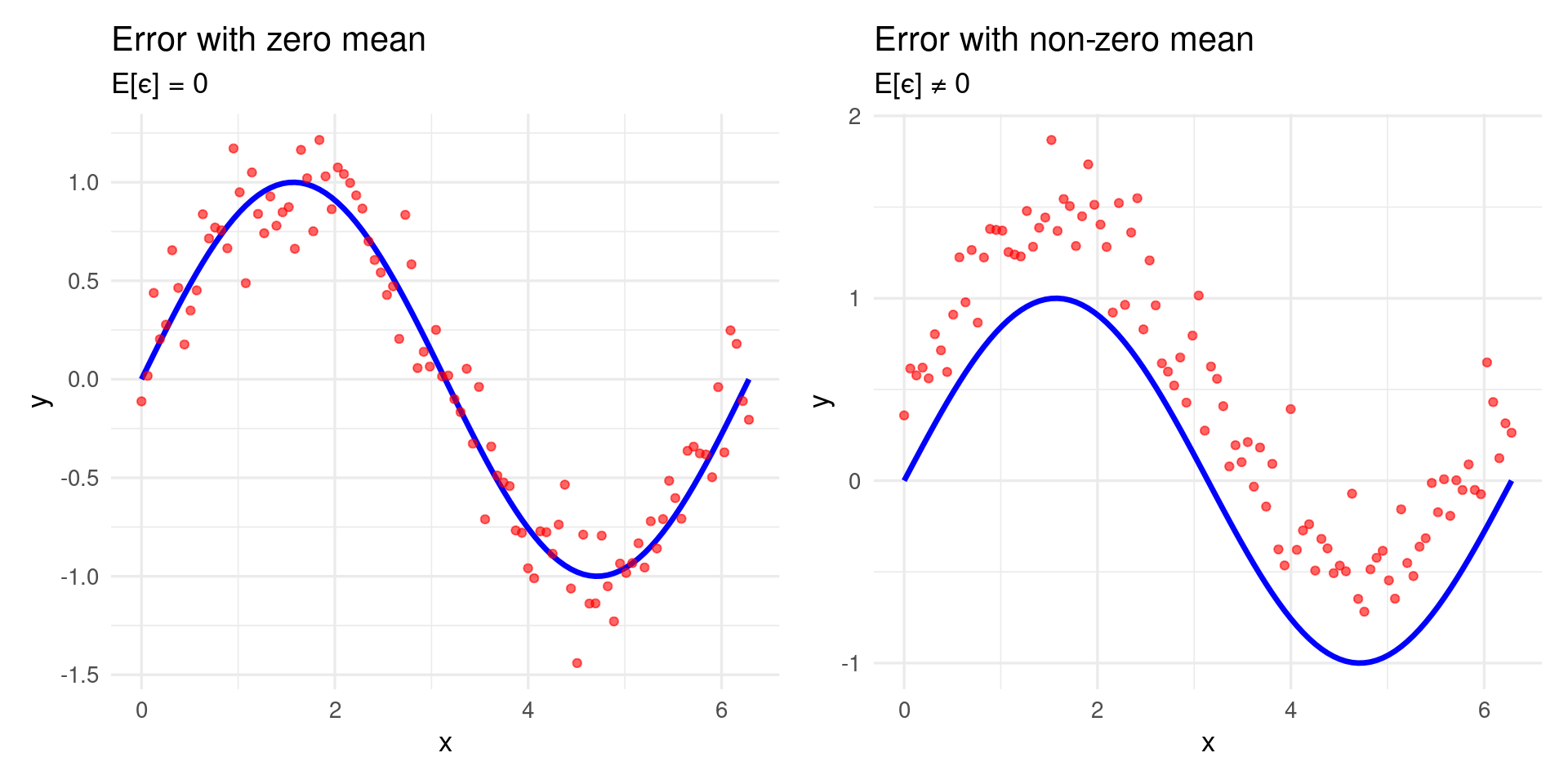
Por que esperança do erro é zero, \(E(\epsilon) = 0\)?
que significa que o ruído não afeta o valor esperado de \(y\) dado \(\dot{\mathbf{x}}\), preservando a imparcialidade do modelo.
Implicações
\(E[\epsilon] = 0\) significa que o ruído é não viesado.
Se \(E[\epsilon] \ne 0\), o modelo teria um viés sistemático.
O modelo capturaria uma média incorreta de \(y\), afetando predições.
As Duas Culturas
Predição
Exemplo 1:
Valor real: \(f(x) = 170\)
Ruído: \(\epsilon \sim \mathcal{N}(0, 35)\)
Modelo:
\[
y = 170 + \epsilon
\]
Então:
\[
E[y] = 170 + E[\epsilon] = 170 + 0 = 170
\]
O valor médio observado coincide com o valor real.
As Duas Culturas
Predição
Exemplo 2: Ruído com Viés
Valor real: \(f(x) = 170\)
Ruído: \(\epsilon \sim \mathcal{N}(10, 35)\)
Modelo:
\[
y = 170 + \epsilon
\]
Então:
\[
E[y] = 170 + + E[\epsilon] = 170 + 10 = 180
\]
Neste caso, a média observada está deslocada. O modelo possui viés sistemático.
As Duas Culturas
Predição
library(ggplot2)library(patchwork)set.seed(123)n <-100x <-seq(0, 2*pi, length.out = n)g_x <-sin(x)# Case 1: Error with zero mean (no bias)eps_zero <-rnorm(n, mean =0, sd =0.2)y_zero <- g_x + eps_zerodf_zero <-data.frame(x = x, g_x = g_x, y = y_zero)p1 <-ggplot(df_zero, aes(x = x)) +geom_line(aes(y = g_x), color ="blue", size =1.2) +geom_point(aes(y = y), alpha =0.6, color ="red") +labs(title ="Error with zero mean",subtitle ="E[ϵ] = 0",x ="x", y ="y") +theme_minimal(base_size =13)# Case 2: Error with non-zero mean (biased)eps_bias <-rnorm(n, mean =0.5, sd =0.2)y_bias <- g_x + eps_biasdf_bias <-data.frame(x = x, g_x = g_x, y = y_bias)p2 <-ggplot(df_bias, aes(x = x)) +geom_line(aes(y = g_x), color ="blue", size =1.2) +geom_point(aes(y = y), alpha =0.6, color ="red") +labs(title ="Error with non-zero mean",subtitle ="E[ϵ] ≠ 0",x ="x", y ="y") +theme_minimal(base_size =13)# Mostrar lado a ladop1 + p2
As Duas Culturas
Predição
As Duas Culturas
Predição
Exemplo:
Considere uma empresa que está interessada em realizar uma campanha de marketing direto.
O objetivo é identificar indivíduos que responderão positivamente a um mailing, com base em observações de variáveis demográficas medidas em cada indivíduo.
Nesse caso, as variáveis demográficas servem como preditoras, e a resposta à campanha de marketing (positiva ou negativa) serve como o resultado.
A empresa não está interessada em obter um entendimento profundo das relações entre cada preditor individual e a resposta; em vez disso, a empresa simplesmente deseja um modelo preciso para prever a resposta usando os preditores. Esse é um exemplo de modelagem para predição.
Como estimamos \(f\)?
Sempre assumiremos que observamos um conjunto de \(n\) objetos de dados diferentes. Por exemplo, um \(n = 30\), representa que temos uma amostra com \(30\) observações. Com essas observações estimamos um modelo \(g\) que melhor representa \(f\).
Seja \(x_{ij}\) o valor da \(i\)-ésima observação da \(j\)-ésima variável, onde \(i = 1, 2, \ldots, n\) e \(j = 1, 2, \ldots, p\). E seja \(y_i\) o valor observado da variável resposta para a \(i\)-ésima observação. Então, nossos dados consistem em
em que \(\dot{\mathbf{x}}_i = (x_{i1}, x_{i2}, \ldots, x_{ip})^\top\).
Como estimamos \(f\)?
Nosso objetivo é aplicar um método de aprendizagem estatística aos dados para estimar a função desconhecida \(f\).
Em outras palavras, queremos encontrar uma função \(g\), tal que, \(y \approx g(\dot{\mathbf{x}})\) para qualquer observação \((\dot{\mathbf{x}}, y)\).
De modo geral, a maioria dos métodos de aprendizagem estatística para essa tarefa pode ser caracterizada como paramétrica ou não paramétrica.
Como estimamos \(f\)?
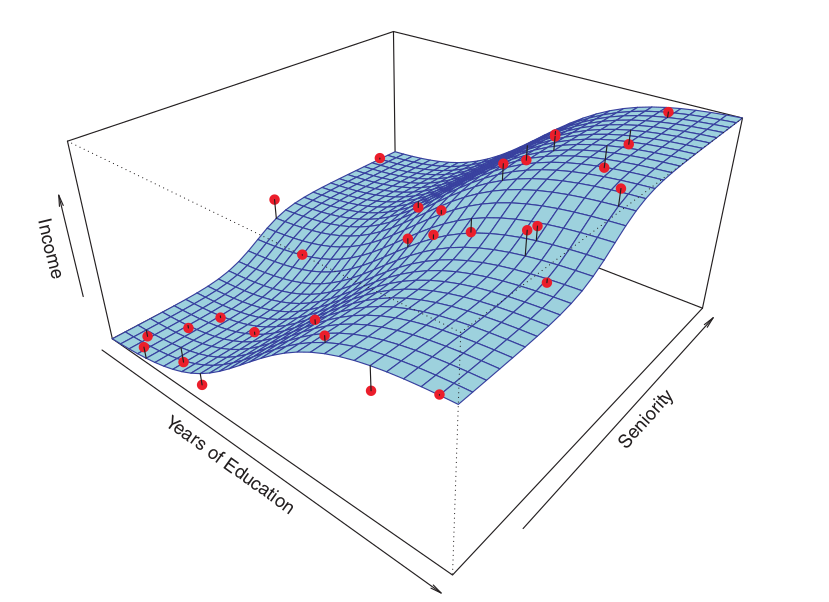
Considere o exemplo abaixo:
O gráfico exibe a renda em função dos anos de educação e senioridade no conjunto de dados Income.
A superfície azul representa a verdadeira relação subjacente entre renda (income), anos de educação (Years of education) e senioridade (seniority), que é conhecida. Os pontos vermelhos indicam os valores observados dessas quantidades para 30 indivíduos.
Como estimamos \(f\)?
Métodos paramétricos
Os métodos paramétricos envolvem uma abordagem baseada em modelo com duas etapas:
Primeira, fazemos uma suposição sobre a forma funcional, ou o formato, de \(f\). Por exemplo, uma suposição muito simples é que \(f\) é linear em \(\mathbf{x}\):
Uma vez que assumimos que \(f\) é linear, o problema de estimar \(f\) é estimar os \(p + 1\) coeficientes \(\beta_0, \beta_1, \ldots, \beta_p\) do modelo.
Como estimamos \(f\)?
Métodos paramétricos
Depois que um modelo é selecionado, precisamos de um procedimento que use os dados para ajustar ou estimar o modelo. No caso do modelo linear, precisamos estimar os parâmetros \(\beta_0, \beta_1, \ldots, \beta_p\). Queremos encontrar valores desses parâmetros tais que
em que \(\epsilon_i\) é o erro aleatório, com \(E[\epsilon_i] = 0\).
Nosso objetivo é estimar \(\hat{\beta}_0, \hat{\beta}_1, \dots, \hat{\beta}_p\) minimizando os erros. Neste caso, vamos minimizar a soma dos quadrados dos resíduos: \[
S(\boldsymbol{\beta}) = \sum_{i=1}^n \left( y_i - (\beta_0 + \beta_1 x_{i1} + \dots + \beta_p x_{ip}) \right)^2
\]
em que, \(\boldsymbol{\beta} = [\beta_0 \, \beta_1\, \ldots\, \beta_p]^\top\), \(e_i = y_i - \hat{y}_i\) é o resíduo para a \(i\)-ésima observação, onde \(\hat{y}_i\) é o valor predito.
Como estimamos \(f\)?
Métodos paramétricos
MQO - mínimos quadrados (ordinários)
A solução é encontrar os valores de \(\hat{\boldsymbol{\beta}} = [\hat{\beta_0} \, \hat{\beta_1}\, \ldots\, \hat{\beta_p}]^\top\) que torna \(S\) mínimo.
Calcula-se as derivadas parciais de \(S(\cdot)\) em relação a cada \(\beta_j\): \[
\frac{\partial S}{\partial \beta_j} = 0, \quad j = 0, 1, \dots, p
\]
Resolve o sistema de equações: \[
\dot{\mathbf{X}}^\top \dot{\mathbf{X}} \hat{\boldsymbol{\beta}} = \dot{\mathbf{X}}^\top \mathbf{y}
\]
\(\dot{\mathbf{X}}\): É chamada de matriz de design, matriz de dados observados, matriz de variáveis de entrada, matriz de variáveis independentes e possui dimensão \((n \times (p+1))\), \(\mathbf{y}\) é o vetor da variável resposta com dimensão \((n \times 1)\), \(\hat{\boldsymbol{\beta}}\) é o Vetor de parâmetros estimados com dimensão \(((p+1) \times 1)\).
Observação: Caso \(\dot{\mathbf{X}}^\top \dot{\mathbf{X}}\) não seja invertível, a equação anterior não possui solução.
Como estimamos \(f\)?
Métodos paramétricos
A abordagem descrita anteriormente é chamada de paramétrica, pois ela reduz o problema de estimar \(f\) à estimativa de um conjunto de parâmetros.
Assumir uma forma paramétrica para \(f\) simplifica o problema de estimar \(f\), porque geralmente é muito mais fácil estimar um conjunto de parâmetros, como \(\beta_0, \beta_1, \ldots, \beta_p\) no modelo linear, do que ajustar uma função completamente arbitrária \(f\).
A desvantagem potencial de uma abordagem paramétrica é que o modelo que escolhemos geralmente não corresponderá à verdadeira forma desconhecida de \(f\).
Se o modelo escolhido estiver muito distante da verdadeira \(f\), nossa estimativa será ruim.
Como estimamos \(f\)?
Métodos paramétricos
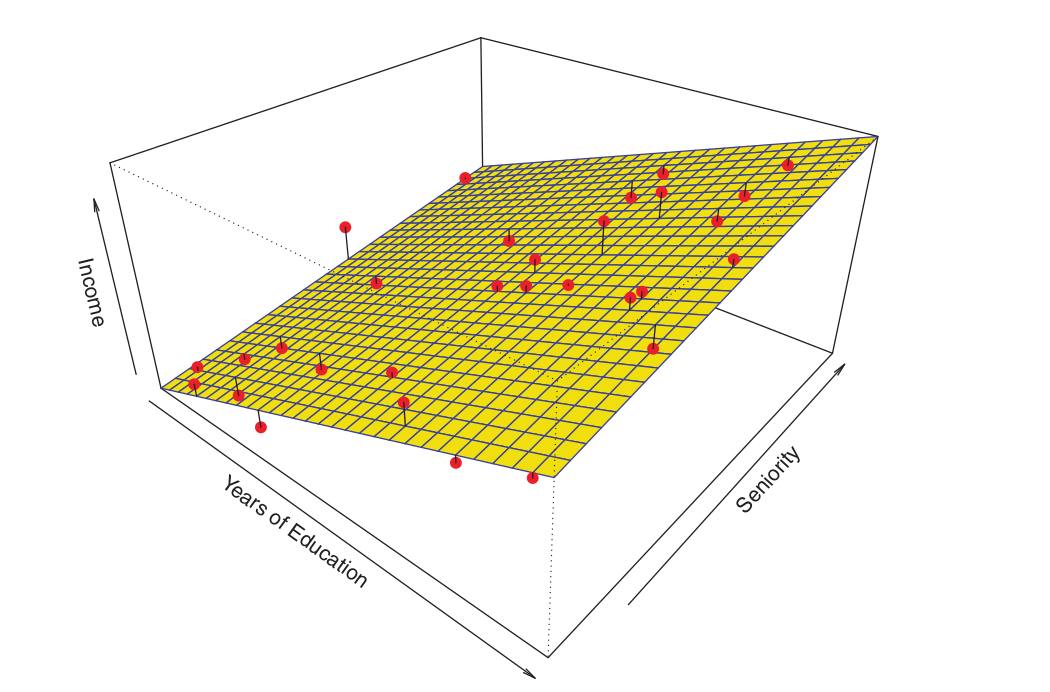
A Figura abaixo mostra um exemplo da abordagem paramétrica aplicada aos dados de Income1.
Como assumimos uma relação linear entre a resposta e os dois preditores, todo o problema de ajuste se reduz a estimar \(\beta_0\), \(\beta_1\) e \(\beta_2\), o que fazemos usando regressão linear por mínimos quadrados.
O ajuste linear apresentado na Figura não é perfeito, no entanto, ainda parece fazer um trabalho razoável ao capturar a relação positiva entre anos de educação e renda, bem como a relação ligeiramente menos positiva entre senioridade e renda.
Como estimamos \(f\)?
Métodos não-paramétricos
Os métodos não-paramétricos não fazem suposições explícitas sobre a forma funcional de \(f\).
Em vez disso, eles buscam uma estimativa de \(f\) que se aproxime o máximo possível dos pontos de dados, sem ser muito irregular ou oscilante.
Ao evitar a suposição de uma forma funcional específica para \(f\), elas têm o potencial de se ajustar com precisão a uma gama mais ampla de formas possíveis para \(f\).
Como estimamos \(f\)?
Métodos não-paramétricos
Qualquer abordagem paramétrica traz consigo a possibilidade de que a forma funcional usada para estimar \(f\) seja muito diferente da verdadeira \(f\), caso em que o modelo resultante não se ajustará bem aos dados. Em contraste, as abordagens não paramétricas evitam completamente esse perigo, já que, essencialmente, nenhuma suposição é feita sobre a forma de \(f\).
No entanto, as abordagens não paramétricas sofrem uma grande desvantagem: como elas não reduzem o problema de estimar \(f\) a um pequeno número de parâmetros, um número grande de observações (muito maior do que o normalmente necessário para uma abordagem paramétrica) é necessário para obter uma estimativa precisa de \(f\).
Como estimamos \(f\)?
Métodos não-paramétricos
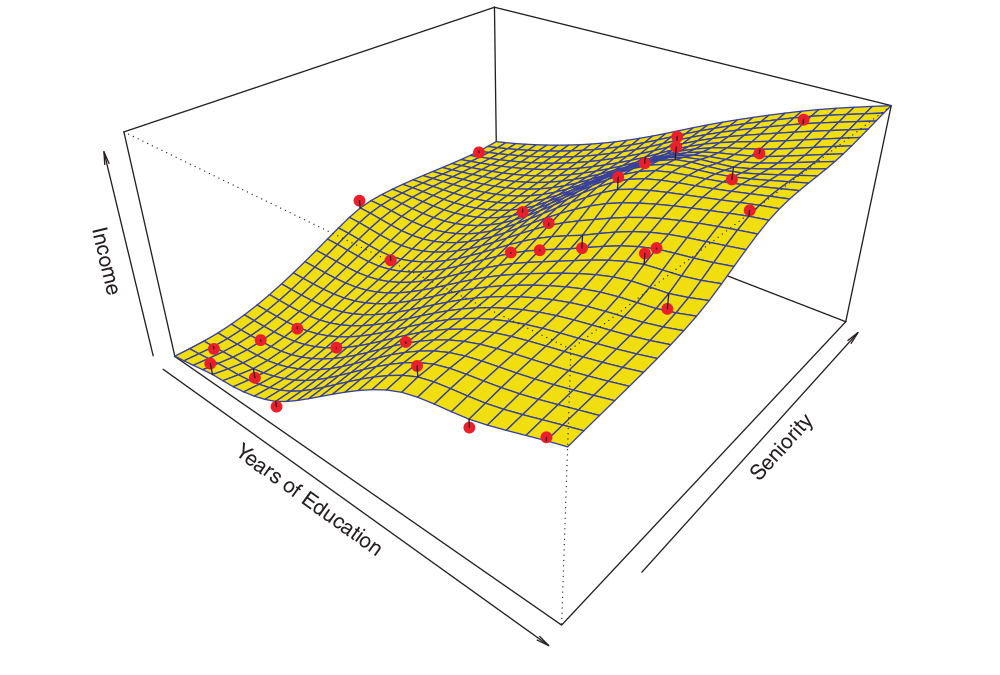
Um exemplo de uma abordagem não paramétrica para ajustar os dados de Income é mostrado na Figura abaixo1.
Como estimamos \(f\)?
Métodos não-paramétricos
Foi utilizado o thin-plate spline1 para estimar \(f\).
Essa abordagem não impõe nenhum modelo pré-especificado sobre \(f\). Em vez disso, ela tenta produzir uma estimativa para \(f\) que esteja o mais próxima possível dos dados observados, sujeita à condição de que o ajuste (a superfície amarela na Figura seja suave).
Nesse caso, o ajuste não paramétrico produziu uma estimativa interessante para \(f\).
Como estimamos \(f\)?
Métodos não-paramétricos
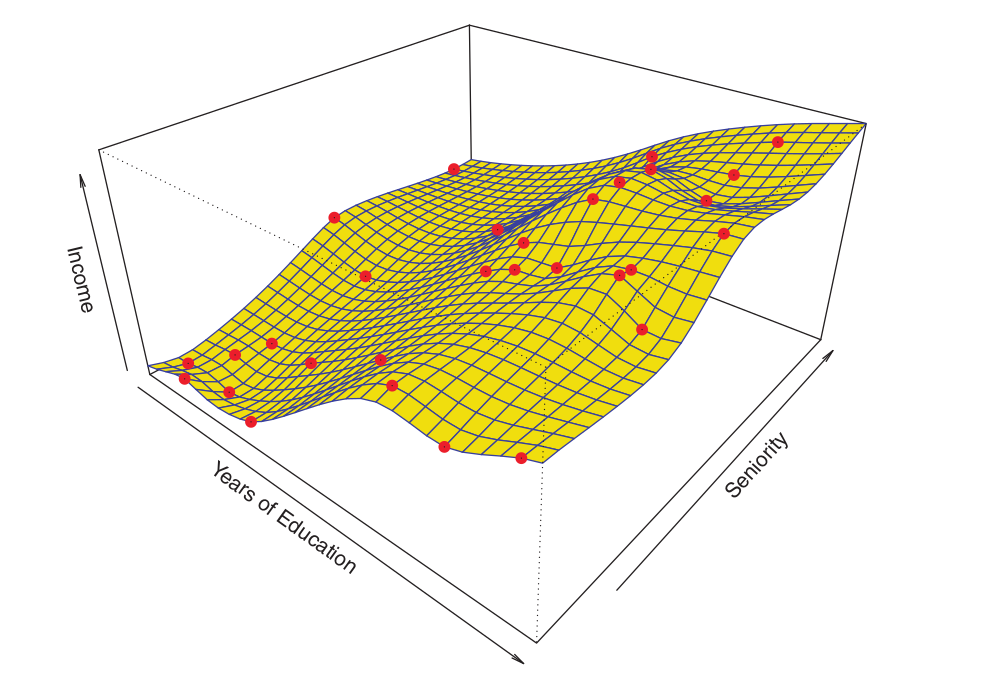
A Figura abaixo mostra o mesmo ajuste de thin-plate spline usando um nível menor de suavidade1, permitindo um ajuste mais irregular.
Como estimamos \(f\)?
Métodos não-paramétricos
A estimativa resultante se ajusta quase perfeitamente aos dados observados!
Este é um exemplo de overfitting (sobreajuste) dos dados,
É uma situação indesejável porque o ajuste obtido não fornecerá estimativas precisas da resposta para novas observações que não faziam parte do conjunto de dados de treinamento original.
Como estimamos \(f\)?
Métodos paramétricos e não-paramétricos
Trade-Off entre Predição e Inferência
O Equilíbrio entre Precisão de Predição e Interpretabilidade do Modelo
Por que escolheríamos usar um método mais restritivo (paramétrico) em vez de uma abordagem mais flexível (não paramétrico)?
Se estamos interessados em inferência, modelos mais restritivos são mais interpretáveis.
Por exemplo, quando a inferência é o objetivo, modelos paramétricos podem ser boas escolhas, pois existirá a possibilidade de entender a relação entre \(Y\) e \(X_1, X_2, \ldots, X_p\).
Trade-Off entre Predição e Inferência
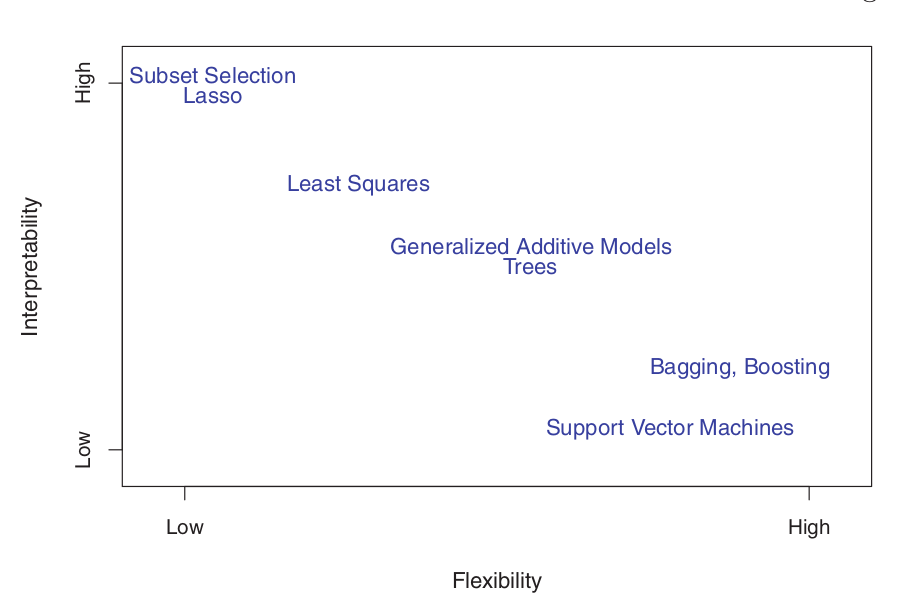
A regressão linear por mínimos quadrados, é relativamente inflexível, mas bastante interpretável.
A regressão lasso, baseia-se no modelo linear, mas usa um procedimento alternativo para estimar os coeficientes \(\beta_0, \beta_1, \ldots, \beta_p\). O novo procedimento é mais restritivo na estimativa dos coeficientes e define alguns deles como exatamente zero. Portanto, nesse sentido, o lasso é uma abordagem menos flexível do que a regressão linear. Ele também é mais interpretável do que a regressão linear, porque, no modelo final, a variável resposta estará relacionada apenas a um pequeno subconjunto dos preditores — aqueles com estimativas de coeficientes diferentes de zero.
Trade-Off entre Predição e Inferência
Os modelos aditivos generalizados (GAMs), estendem o modelo linear para permitir certas relações não lineares. Consequentemente, os GAMs são mais flexíveis e um pouco menos interpretáveis em relação a regressão linear, porque a relação entre cada preditor e a resposta agora é modelada usando uma curva.
Os métodos totalmente não lineares, como bagging, boosting e máquinas de vetores de suporte com kernels não lineares (SVM), são abordagens altamente flexíveis e são mais difíceis de interpretar.
Trade-Off entre Predição e Inferência
Diante do que foi visto até ao momento, estabelecemos que, quando a inferência é o objetivo, há vantagens claras em usar métodos de aprendizagem estatística e relativamente inflexíveis.
Em alguns cenários, no entanto, estamos apenas interessados em predição, e a interpretabilidade do modelo preditivo simplesmente não é relevante.
Nesse cenário, poderíamos esperar que o melhor seria usar o modelo mais flexível disponível.
Muitas vezes, obteremos predições mais precisas usando um método menos flexível.
Esse fenômeno, que pode parecer contra-intuitivo à primeira vista, tem a ver com o potencial de overfitting em métodos altamente flexíveis.
An Introduction to Statistical Learning: with Applications in R, James, G., Witten, D., Hastie, T. and Tibshirani, R., Springer, 2013, link: https://www.statlearning.com/.
Mathematics for Machine Learning, Deisenroth, M. P., Faisal. A. F., Ong, C. S., Cambridge University Press, 2020, link: https://mml-book.com.
Referências
Complementares
An Introduction to Statistical Learning: with Applications in python, James, G., Witten, D., Hastie, T. and Tibshirani, R., Taylor, J., Springer, 2023, link: https://www.statlearning.com/.
Matrix Calculus (for Machine Learning and Beyond), Paige Bright, Alan Edelman, Steven G. Johnson, 2025, link: https://arxiv.org/abs/2501.14787.
