Aprendizagem de Máquina

Probabilidade para Aprendizagem de Máquina

Prof. Jodavid Ferreira

UFPE

Lista de Notação


  • \(X\) ou \(Y\)
  • \(x\) ou \(y\)
  • \(\mathbf{x}\) ou \(\mathbf{y}\)
  • \(\dot{\mathbf{x}}\) ou \(\dot{\mathbf{y}}\)
  • \(\mathbf{X}\) ou \(\mathbf{Y}\)
  • \(\dot{\mathbf{X}}\) ou \(\dot{\mathbf{Y}}\)


    

  • \(p\)
    • 

  • \(n\)
    • 

  • \(i\)
    • 

  • \(j\)
    • 





representam variáveies aleatórias (v.a.);


representam realizações da variáveis aleatórias;


representam vetores aleatórios;


representam realização de vetores aleatórios;


representam matrizes aleatórios;


representam realização de matrizes aleatória;




dimensão das \(features\), variáveis


tamanho da amostra


\(i\)-ésima observação, instância


\(j\)-ésima \(feature\), variável








Probabilidade




Na realização de um fenômeno aleatório, é comum termos interesse em uma ou mais variáveis quantitativas. Essas quantidades são chamadas de variáveis aleatórias.







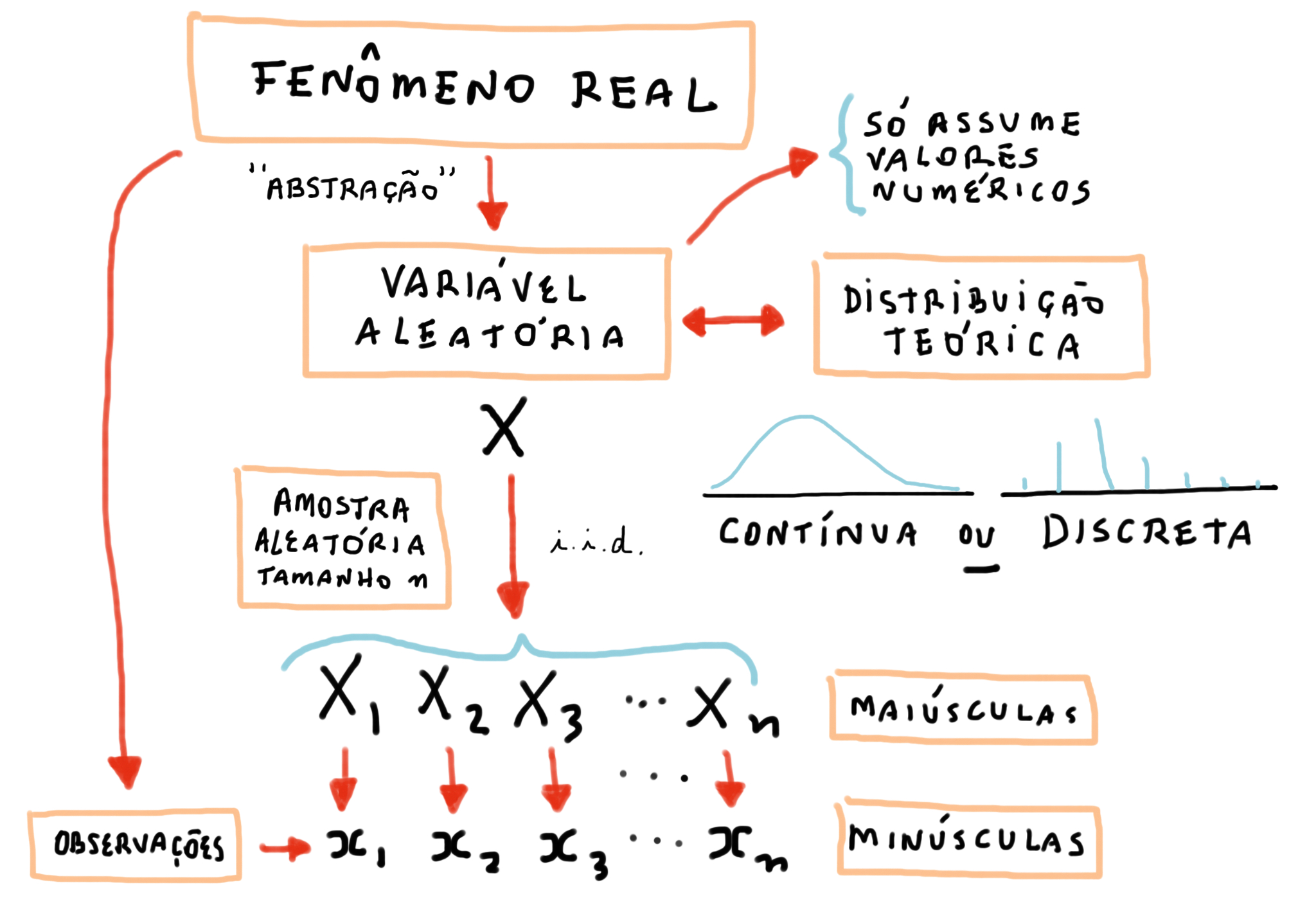
O conhecimento de variáveis aleatórias é muito importante, pois permite a modelagem probabilística de fenômenos da vida real.






Probabilidade







Espaço Amostral





O espaço amostral, que podemos representar por \(\Omega\), é o conjunto de todos os possíveis resultados de um experimento aleatório.





Exemplo:



    

  • Lançamento de um dado honesto de seis faces: \(\\\) \(\Omega\) = {1, 2, 3, 4, 5, 6}
    • 

  • Lançamento de uma moeda: \(\\\) \(\Omega\) = {Cara, Coroa}
    • 







O espaço amostral deve incluir todos os resultados possíveis e é a base para a definição de eventos e cálculos de probabilidades.






Probabilidade







Ponto Amostral





Um ponto amostral é um resultado individual em um espaço amostral de um experimento aleatório, e é denotado genericamente por \(w\). Assim, escrevemos que \(w \in \Omega\) para indicar que o elemento \(w\) está em \(\Omega\).





Exemplo:



    

  • Lançamento de uma moeda:

      

    • Espaço Amostral \(\rightarrow\) \(\Omega\) = {Cara, Coroa}
      • 

    • Pontos Amostrais: Cara, Coroa
      • 

    • 







Cada ponto amostral representa uma das possíveis observações após a realização do experimento.






Probabilidade







Evento





Um evento é um subconjunto do espaço amostral que descreve um ou mais resultados possíveis de um experimento aleatório.





Exemplo:



    

  • Lançamento de um dado honesto de seis faces:

      

    • Espaço Amostral \(\rightarrow\) \(\Omega\) = {1, 2, 3, 4, 5, 6}
      • 

    • Evento A: Obter um número par \(\\\) A = {2, 4, 6}
      • 

    • 







Os eventos são a base para a análise de probabilidades e são definidos como subconjuntos do espaço amostral.






Probabilidade












Probabilidade










Definição 1:


Um evento \(A\) ao qual atribuímos uma probabilidade será chamado evento aleatório.








Seja \(\mathcal{A}\) a classe dos eventos aleatórios (conjunto de eventos aleatórios), temos as seguintes propriedades para \(\mathcal{A}\):





    

  • A1. \(\Omega \in \mathcal{A}\);
    • 

  • A2. Se \(A \in \mathcal{A}\), então \(A^{c} \in \mathcal{A}\);
    • 

  • A3. Se \(A \in \mathcal{A}\) e \(B \in \mathcal{A}\), então \(A \cup B \in \mathcal{A}\).
    • 







Probabilidade









Definição 2:



Uma classe \(\mathcal{A}\) de subconjuntos de um conjunto não-vazio \(\Omega\) satisfazendo A1, A2 e A3’ é chamada de \(\sigma\)-álgbera de subconjuntos de \(\Omega\).









    

  • A3’. Se \(A_n \in \mathcal{A}\) para \(n=1,2,\ldots\), então \(\cup_{n=1}^{\infty}A_n \in \mathcal{A}\);
    • 



Assim, temos que uma \(\sigma\)-álgebra é fechada para um número enumerável de aplicações das operações \(\cup\), \(\cap\) e \(^c\). E seja \(\mathcal{A}\) uma \(\sigma\)-álgebra, então:




P1. Se \(A, B \in \mathcal{A}\), temos que \(A-B = A \cap B^c \in \mathcal{A}\);


P2. Se \(A, B \in \mathcal{A}\), temos que \(A \Delta B = (A \cap B^c)\cup (B \cap A^c) \in \mathcal{A}\)


P3. Seja \(\{A_n\}_{n \geq 1}\), uma sequência de elementos em \(\mathcal{A}\), temos que \(\cup_{n=1}^{\infty}A_n \in \mathcal{A}\) e \(\cap_{n=1}^{\infty}A_n \in \mathcal{A}\);






Probabilidade










Definição 3:



Seja \(\Omega\) um conjunto não-vazio e \(\mathcal{A}\) uma \(\sigma\)-álgebra de subconjuntos de \(\Omega\). A função \(P: \mathcal{A} \rightarrow \mathbb{R}\) é dita probabilidade se satisfaz os seguintes axiomas:









Ax1) \(P(A)\geq 0\);


Ax2) \(P(\Omega) = 1\);


Ax3) ( \(\sigma\) -aditividade) Seja \(\{A_n\}_{n \geq 1}\), uma sequência de elementos em \(\mathcal{A}\), tal que \(A_i \cap A_j = \emptyset, \forall i \neq j\), isto é, disjuntos 2 a 2, então \(P(\cup_{n=1}^\infty A_n) = \sum_{n=1}^\infty A_n\).






Probabilidade










Definição 4:



Um espaço de probabilidade é uma estrutura \((\Omega,\mathcal{A}, P)\) em que \(\Omega \neq \emptyset\), \(\mathcal{A}\) é uma \(\sigma\)-álgebra de subconjuntos de \(\Omega\) e \(P:\mathcal{A} \rightarrow \mathbb{R}\) é uma probabilidade em \(\mathcal{A}\).















Probabilidade







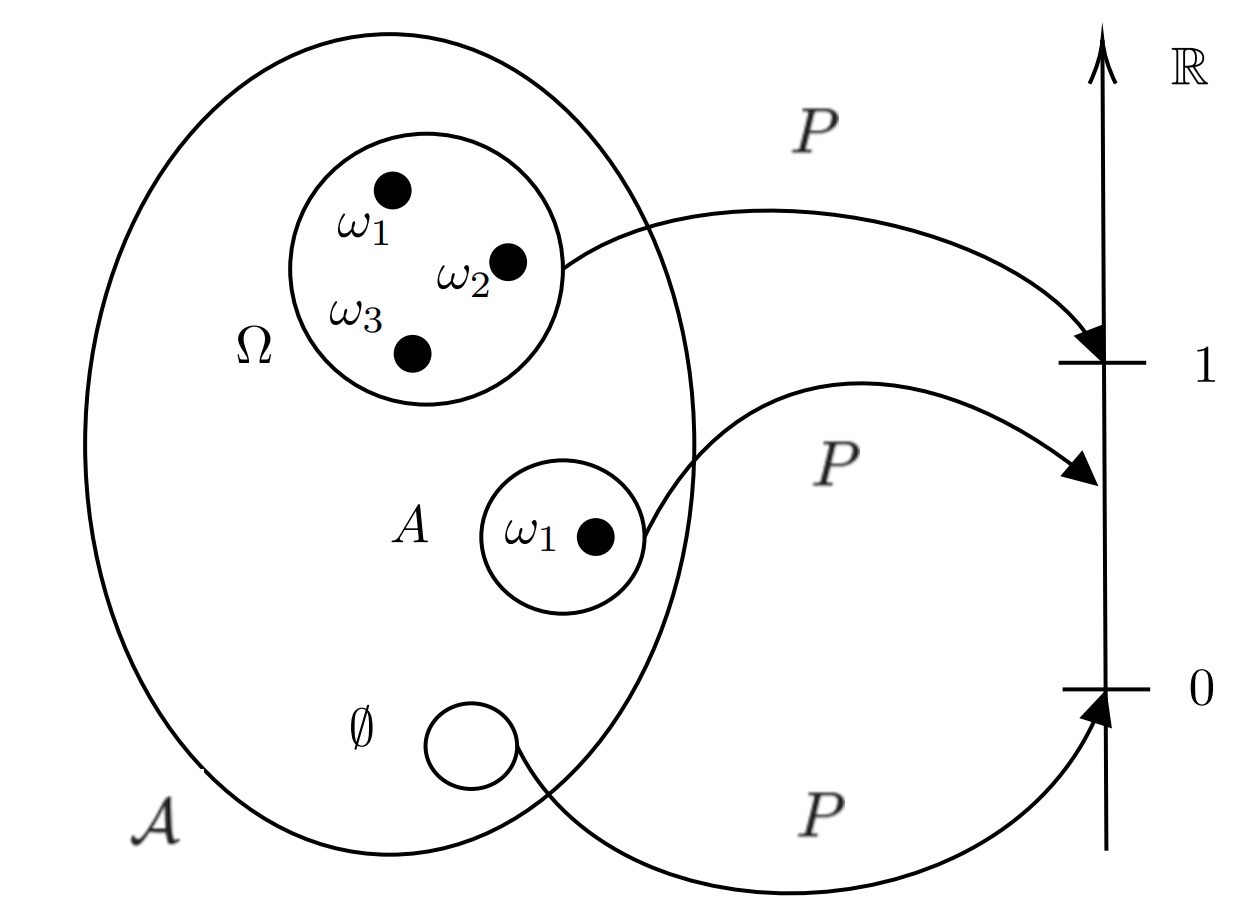
Dado os axiomas de Kolmogorov, é possível definir as seguintes propriedades:




P1) \(P(A) \geq 1 - P(A^c)\);


P2) \(0 \leq P(A) \leq 1\);


P3) Se \(A \subset B\), então \(P(A) \leq P(B)\);


P4) \(P(\cup_{i=1}^{n}A_i) \leq \sum_{i=1}^{n}P(A_i)\) (subaditividade finita);


P5) \(P(\cup_{n=1}^{\infty}A_n) \leq \sum_{n=1}^{\infty}P(A_n)\) ( \(\sigma\) -subaditividade);


P6) (continuidade de probabilidade) Se \(A_n \uparrow A\), então \(P(A_n) \uparrow P(A)\). Se \(A_n \downarrow A\), então \(P(A_n) \downarrow P(A)\).






Probabilidade










Exemplo:




Se \(P(A) = 1/3\) e \(P(B^c) = 1/4\), \(A\) e \(B\) podem ser mutuamente exclusivos, ou seja, eventos disjuntos?


 
 
 
 
 
 
 
 










Probabilidade










Exemplo:




Se \(P(A) = 1/3\) e \(P(B^c) = 1/4\), \(A\) e \(B\) podem ser mutuamente exclusivos, ou seja, eventos disjuntos?




Solução:


\(P(B) = 1- P(B^c) = \dfrac{3}{4}\\\)


Considerando que \(A\) e \(B\) são mutuamente exclusivos, temos


\(P(A \cup B) = P(A) + P(B) = \dfrac{1}{3} + \dfrac{3}{4} = \dfrac{13}{12} > 1.\\\)


Logo, \(A\) e \(B\) não são mutuamente exclusivos, ou seja, existe interseção entre eles, \(A \cap B \neq \emptyset\).












Probabilidade










Exemplo:




Sejam \(A\) e \(B\) eventos mutuamente exclusivos tais que \(P(A) = 0,5\) e \(P(B) = 0,4\).


a) Calcule \(P(A \cup B)\).


b) Calcule \(P(B \cap A^c)\).


 
 
 
 
 
 










Probabilidade










Exemplo:




Sejam \(A\) e \(B\) eventos mutuamente exclusivos tais que \(P(A) = 0,5\) e \(P(B) = 0,4\).


a) Calcule \(P(A \cup B)\).


b) Calcule \(P(B \cap A^c)\).







Solução:


Do enunciado, concluímos que \(A \cap B = \emptyset\). Logo,


    

  1. \(P(A \cup B) = P(A) + P(B) = 0,5 + 0,4 = 0,9\)
    2. 

  2. \(P(B \cap A^c) = P(B) - P(A \cap B) = 0,4 - 0  = 0,4\)
    3. 













Probabilidade Condicional







Seja \((\Omega, \mathcal{A},P)\) espaço de probabilidade e seja \(A \in \mathcal{A}\), tal que, \(P(A) > 0\). Seja \(B \in \mathcal{A}\), definimos a probabilidade condicional de \(B\) dado \(A\) como


\[\begin{align}
P(B|A) = \dfrac{P(A \cap B)}{P(A)}.
\end{align}\]




Da equação acima, temos que


\[\begin{align}
P(A \cap B) = P(A)P(B|A).
\end{align}\]




Generalizando, temos que


\[\begin{align}
P \left(\bigcap_{j=1}^{n}A_j \right) = \prod_{j=1}^{n}P \left( A_j | \bigcap_{i=1}^{n-1}A_i\right).
\end{align}\]






Probabilidade Condicional









Teorema da Probabilidade Total





Seja \(\{A_n\}_{n \geq 1}\) sequência de eventos em \(\mathcal{A}\) que formam partição em \(\Omega\), ou seja, são eventos disjuntos 2 a 2, então


\[\begin{align}
P(B) = \sum_{n} P(A_n) P(B | A_n), \forall B \in \mathcal{A}.
\end{align}\]









Demonstração:


Temos que \(\Omega = \cup_n A_n\), união disjunta. Logo,


\[\begin{align}
P(B) & = P(\Omega \cap B) = P (\cup_n A_n \cap B) = \nonumber \\
& = P(\cup_n (A_n \cap B)) = \sum_n P(A_n \cap B) = \sum_n P(B | A_n) P(A_n)
\end{align}\]










Probabilidade Condicional






Do Teorema anterior, é possível calcular a probabilidade de \(A_n\) dado a ocorrência de B:


\[\begin{align}
P(A_n | B) = \dfrac{P(A_n \cap B)}{P(B)} = \dfrac{P(A_n)P(B|A_n)}{\sum_n P(B|A_n)P(A_n)}
\end{align}\]





Esta é a Probabilidade de Bayes, a qual é útil quando conhecemos as probabilidades dos \(A_n\)’s e as probabilidades condicionais de \(B\) dado \(A_n\), mas não conhecemos diretamente a probabilidade de \(B\).





Para \(A \in \mathcal{A}\), com \(P(A) > 0\), a função \(P_A:\mathcal{A} \rightarrow [0,1]\) definida por \(P_A(B) = P(B | A)\) é uma probabilidade.






Probabilidade Condicional






Segue a análise dos axiomas:





Ax1) \(P_A(\Omega) = P(\Omega|A) = \dfrac{P(A \cap \Omega)}{P(A)} = 1\);




Ax2) \(P_A \geq 0\), é válido porque \(P \geq 0\);




Ax3) Seja \(\{B_n\}_{n \geq 1}\) sequência de elementos disjuntos em \(\mathcal{A}\). Então, \(P_A(\cup_{n=1}^{\infty}B_n) = P(\cup_{n=1}^{\infty}B_n | A) = \dfrac{P(A \cap \cup_{n=1}^{\infty} B_n)}{P(A)} =\)


\(\sum_{n=1}^{\infty} P(B_n | A) = \sum_{n=1}^{\infty} P_A(B_n)\);



























Variáveis Aleatórias




Dado um fenômeno aleatório qualquer, com um certo espaço de probabilidade, desejamos estudar a estrutura probabilística de quantidades associadas a esse fenômeno.










Definição 5:



Seja \((\Omega,\mathcal{A}, P)\) um espaço de probabilidade. Denominamos de variável aleatória, qualquer função \(X:\Omega \rightarrow \mathbb{R}\) tal que


\[\begin{align}
X^{-1} (I) = \{ \omega \in \Omega : X(\omega) \in I\} \in \mathcal{A},
\end{align}\]


para todo intervalo \(I \subset \mathbb{R}\). Em outras palavras, \(X\) é variável aleatória se sua imagem inversa para intervalos \(I \subset \mathbb{R}\) pertencem a \(\sigma\)-álgebra \(\mathcal{A}\).










Função de Distribuição









Definição 6:



Seja \(X\) uma variável aleatória em \((\Omega,\mathcal{A}, P)\), sua função de distribuição é definida por


\[\begin{align}
F_X(x) = P(X \in (\infty,x]) = P(X \leq x),
\end{align}\]


com \(x\) percorrendo todos os reais.











Propriedades da Função de Distribuição:




F1) \(\lim\limits_{x \to -\infty} F_X(x) = 0\) e \(\lim\limits_{x \to +\infty} F_X(x) = 1\);


F2) \(F_X\) é contínua a direita;


F3) \(F_X\) é não decrescente, isto é, \(F_X(x) \leq F_X(y)\) sempre que \(x \leq y\), \(\forall x,y \in \mathbb{R}\).






Probabilidade


Variável Aleatória discreta e Função de Probabilidade









Definição 7:



Uma variável aleatória é definida como discreta, se assume somente uma quantidade enumerável de valores. Sendo \(X\) uma variável aleatória com valores \(x_1, x_2, \ldots\), temos para \(i = 1,2,\ldots\),


\[\begin{align}
p(x_i) = P( X  = x_i) = P({\omega \in \Omega : X(\omega) = x_i}).
\end{align}\]








Propriedades da Função de Probabilidade:




fp1) \(0 \leq p(x_i) \leq 1, \forall i = 1,2,\ldots\);


fp2) \(\sum\limits_i p(x_i) = 1\);


com a soma percorrendo todos os possíveis valores.






Probabilidade


Variável Aleatória contínua e Função Densidade









Definição 8:



Uma variável aleatória \(X\) em \((\Omega, \mathcal{A}, P)\), com função de distribuição \(F_X\) é classificada como contínua, se existir uma função não negativa \(\mathcal{f}\) tal que:


\[\begin{align}
F_X(x) = \int_{-\infty}^{x} \mathcal{f}(\omega)d\omega, \text{ para todo } x \in \mathbb{R}.
\end{align}\]


A função \(\mathcal{f}\) é denominada função densidade.








Propriedades da Função Densidade:




fd1) \(\mathcal{f}(x) \geq 0, \forall x \in \mathbb{R}\);


fd2) \(\int_{-\infty}^{\infty} \mathcal{f}(x)dx = 1\).






Vetores Aleatórios









Definição 9:



Seja \((\Omega,\mathcal{A}, P)\) um espaço de probabilidade, então, uma função \(\mathbf{x}  = (X_1, \ldots, X_p): \Omega \rightarrow \mathbb R^p\) que é \(\mathcal A\)-mensurável, é dito ser vetor aleatório. Temos que \(\mathbf{x}\) é vetor aleatório, se


\[\begin{align}
\mathbf{x}^{-1} (\boldsymbol H) \in \mathcal{A}, \forall \boldsymbol H \in \mathbb R^p
\end{align}\]


Em outras palavras, \(\mathbf{x}\) é vetor aleatório se para cada \(i = 1,\ldots,p\) e \(H_i \subset \mathbb R\), tivermos


\[\begin{align}
X_i^{-1} (H_i) \in \mathcal{A},
\end{align}\]


ou seja, cada \(X_i\) é variável aleatória.










Funções de Distribuições no \(\mathbb{R}^p\)





 







Definição 10:



Seja \(F_{\mathbf{x}}: \mathbb R^p \rightarrow \mathbb [0,1]\) uma função definida como \(F_{\mathbf{x}}(\dot{\mathbf{x}}) = \mu_{\mathbf{x}}(S_{\mathbf{x}})\), em que \(S_{\mathbf{x}} = (-\infty,x_1]\times\cdots\times(\infty,x_p]\) o conjunto obtido a partir de \({\mathbf{x}} = (X_1, \ldots, X_p)\). Então, \(F_{\mathbf{x}}\) é a função de distribuição conjunta de \(X_1, \ldots, X_p\) ou simplesmente função de distribuição de \(\mathbf{x}\).










Funções de Distribuições no \(\mathbb{R}^p\)






Seja \({\mathbf{x}}\) um vetor aleatório em \((\Omega, \mathcal A, P)\) então, para qualquer \(\dot{\mathbf{x}} \in \mathbb R^p\), \(F_{\mathbf{x}}(\dot{\mathbf{x}})\) satisfaz as seguintes propriedades:




FC1) \(F_{\mathbf{x}}(\dot{\mathbf{x}})\) é não decrescente em cada uma das suas coordenadas.




FC2) \(F_{\mathbf{x}}(\dot{\mathbf{x}})\) é contínua a direita em cada uma das suas coordenadas;




FC3) Se para algum \(j\), \(x_j \rightarrow -\infty\), então \(F_{\mathbf{x}}(\dot{\mathbf{x}}) \rightarrow 0\) e \(\\\) \(\hspace{1.5cm}\) Se para todo \(j\), \(x_j \rightarrow +\infty\), então \(F_{\mathbf{x}}(\dot{\mathbf{x}}) \rightarrow 1\)




FC4) \(F_{\mathbf{x}}(\dot{\mathbf{x}})\) é tal que, \(\forall a_i, b_i \in \mathbb R\), \(a_i < b_i\), \(1 \leq i \leq p\), temos \(\\\) \[P(a_1 < X_1 \leq b_1, \ldots, a_p < X_p \leq b_p) \geq 0. \]






Vetor aleatório discreto










Definição 11:



Dizemos que \(\mathbf{x}\) é um vetor aleatório discreto, quando existir \(S \subset \mathbb R^p\) contável (finito ou enumerável) tal que \(\mu_{\mathbf{x}}(S) = 1\). Neste caso, a função


\[\begin{align}
P_{\mathbf{x}}({\dot{\mathbf{x}}})  = \mu_{\mathbf{x}}(\left\lbrace \dot{\mathbf{x}} \right\rbrace) = P( \mathbf{x} = \dot{\mathbf{x}}), \forall{\dot{\mathbf{x}}} \in \mathbb R^p
\end{align}\]


é chamada função de probabilidade de \(\mathbf{x}\).


Temos que \(\mathbf{x} = (X_1, \ldots, X_p)\) é vetor aleatório discreto, se e somente se, cada variável \(X_i\), \(i = 1,\ldots,p\) é discreto.










Vetor aleatório discreto













Dado \(\mathbf{x} = (X_1, \ldots, X_p)\) vetor aleatório, temos que





\[[X_1 \leq x_1, \ldots,X_i \leq x_i, \ldots, X_p \leq x_p] \uparrow [X_i \leq x_i], \,  x_j \uparrow +\infty, \, \forall j \neq i\]


Logo,


\[P(X_1 \leq x_1, \ldots,X_i \leq x_i, \ldots, X_p \leq x_p) \uparrow P(X_i \leq x_i), \,  x_j \uparrow +\infty, \, \forall j \neq i\]


ou seja,


\[\lim\limits_{x_j \to +\infty \\ \forall j \neq i} F_{\mathbf{x}}({\dot{\mathbf{x}}}) = P (X_i \leq x_i) = F_{X_i}(x_i)\]


\(F_{X_i}(x_i)\) é chamada funçao de distribuição marginal de \(X_i\), \(i = 1, \ldots, p\).










Vetor aleatório discreto




Neste caso temos








Função de distribuição marginal



Seja \(X_i\) com \(i = 1, \ldots, p\) a função de distribuição marginal é dada por


\[\begin{align}
F_{X_i}(x_i) = P (X_i \leq x_i)
\end{align}\]












Função de probabilidade marginal



Seja \(X_i\) com \(i = 1, \ldots, p\) a função de probabilidade marginal é dado por


\[\begin{align}
P_{X_i}(x_i) = P (X_i = x_i)
\end{align}\]










Vetor aleatório discreto





Função de probabilidade conjunta da Poisson



A função de probabilidade conjunta é dada por: \[\begin{align}
P(\mathbf{x}) = & P(X_1 = x_1, X_2 = x_2, \ldots, X_p = x_p) \\
    = & \exp \left( -\sum_{i=1}^p \theta_i \right) \prod_{i=1}^p \frac{\theta_i^{x_i}}{x_i!} \sum_{i=0}^s \prod_{j=1}^p \binom{x_j}{i} i! \left( \frac{\theta_0}{\prod_{i=1}^p \theta_i} \right)^i
\end{align}\] onde \(s = \min(x_1, x_2, \ldots, x_p)\).





    

  • Marginalmente, cada \(X_i\) segue uma distribuição de Poisson com parâmetro \(\theta_0 + \theta_i\).
    • 

  • O parâmetro \(\theta_0\) é a covariância entre todos os pares de variáveis aleatórias.
    • 

  • Se \(\theta_0 = 0\), então as variáveis são independentes.
    • 







Vetor aleatório contínuo












Definição 12:



Dizemos que \(\mathbf{x}\) é um vetor aleatório que possui distribuições absolutamentes contínuas se existir \(f_{\mathbf{x}} \geq 0\) tal que, \(\forall H  \in \mathbb R^p\), temos


\[\begin{align}
F_{\mathbf{x}}(H)  = \idotsint\limits_H  f_{\mathbf{x}}(x_1, \ldots, x_p)dx_1\ldots dx_p
\end{align}\]


em que, \(f_{\mathbf{x}}\) é chamada função densidade de \(\mathbf{x}\).










Vetor aleatório contínuo




Neste caso temos










Função de distribuição marginal



Seja \(X_i\) com \(i = 1, \ldots, p\) a função de distribuição marginal é dada por


\[\begin{align}
F_{X_i}(x_i) = P (X_i \leq x_i)
\end{align}\]












Função densidade marginal



Seja \(X_i\) com \(i = 1, \ldots, p\) a função densidade marginal é dado por


\[\begin{align}
P_{X_i}(x_i) = f_{X_i}(x_i)
\end{align}\]










Vetor aleatório contínuo





Distribuição Normal Multivariada



A distribuição normal multivariada para um vetor aleatório \(\mathbf{x} \in \mathbb{R}^p\) com média \(\boldsymbol{\mu}\) e matriz de covariância \(\boldsymbol{\Sigma}\) é dada por:


\[
f\mathbf{x}(\dot{\mathbf{x}}) = \frac{1}{(2\pi)^{p/2} |\boldsymbol{\Sigma}|^{1/2}} \exp \left( -\frac{1}{2} (\dot{\mathbf{x}} - \boldsymbol{\mu})^\top \boldsymbol{\Sigma}^{-1} (\dot{\mathbf{x}} - \boldsymbol{\mu}) \right)
\]


Onde:


    

  • \(\mathbf{x}\): Vetor aleatório de dimensão \(p\).
    • 

  • \(\boldsymbol{\mu}\): Vetor de médias (\(p \times 1\)).
    • 

  • \(\boldsymbol{\Sigma}\): Matriz de covariância (\(p \times p\)), simétrica e definida positiva.
    • 

  • \(|\boldsymbol{\Sigma}|\): Determinante de \(\boldsymbol{\Sigma}\).
    • 







Independência






Por Magalhães, em seu livro “Probabilidade e Variáveis Aleatórias”, a propriedade denominada independência de eventos é uma propriedade particular de grande importância. Ela permite, muitas vezes, separar o experimento em partes mais simples de serem estudadas e, assim, possibilitar uma enorme simplificação nos cálculos probabilísticos de interesse.








Definição 13:



Seja \((\Omega, \mathcal{A}, P)\) espaço de probabilidade. Dizemos que os eventos \(A,B \in \mathcal{A}\) são independentes, se




\[\begin{align}
P(A \cap B) = P(A)P(B)
\end{align}\]










Independência










Proposição 1:



Se \(P(A) > 0\), então temos que \(P(B|A) = P(B)\)






Pela probabilidade condicional temos que


\[\begin{align}
P(B|A) = \dfrac{P(A \cap B)}{P(A)} = \dfrac{P(A)P(B)}{P(A)}
\end{align}\]


assim,


\[\begin{align}
P(B|A) = P(B)
\end{align}\]










Independência









Definição 14:



Seja \(\mathcal{I} \neq \emptyset\) um conjunto arbitrário de índices e seja a classe \(\zeta = \{A_s:s \in \zeta \} \in \mathcal{A}\). Dizemos que \(\zeta\) é uma classe de eventos independentes quando para todo conjunto de índices \(s_1, s_2, \ldots \in \mathcal{I}\) tivermos


\[\begin{align}
P( \cap_{i=1}^{p} A_{s_i}) = \prod_{i=1}^{p} P (A_{s_i})
\end{align}\]






Por exemplo, \(A,B,C \in \mathcal{A}\) são independentes quando satifaz:


    

  • \(P(A \cap B) = P(A)P(B);\)
    • 

  • \(P(B \cap C) = P(B)P(C);\)
    • 

  • \(P(A \cap C) = P(A)P(C);\)
    • 

  • \(P(A \cap B \cap C) = P(A)P(B)P(C);\)
    • 







Independência




Sendo assim, para Funções de distribuição com vetores aleatórios temos os seguintes critérios de independência:





Funções de distribuição



c1) Se \(X_1, \ldots, X_p\) são independentes, então


\[\begin{align}
F_{X_1, \ldots, X_p}(x_1, \ldots, x_p) = \prod\limits_{i=1}^p F_{X_i}(x_i), \forall (x_1, \ldots, x_p) \in \mathbb R^p
\end{align}\]




c2) Reciprocamente, se existem funções \(F_1, \ldots, F_p\) tais que


\[\begin{align}
\lim\limits_{x \rightarrow + \infty} F_i(x) = 1, \forall i \text{ e }
\end{align}\]


\(F_{X_1,\ldots,X_p}(x_1,\ldots,x_p) = \prod\limits_{i=1}^pF_i(x_i), \forall (x_1,\ldots,x_p) \in \mathbb R^p,\) então \(X_1, \ldots, X_p\) são independentes e \(F_i = F_{X_i}, \forall i = 1,\ldots,p\).










Independência




e para as funções de probabilidade e funções densidades temos:





Função de probabilidade



Assim temos que para o Caso Discreto, se \(X_1, \ldots, X_p\) são independentes, então


\[\begin{align}
P(X_1 = x_1, \ldots, X_p = x_p) = \prod\limits_{i=1}^pP(X_i = x_i)
\end{align}\]







Função densidade



E no caso absolutamente contínuo, se \(X_1, \ldots, X_p\) são independentes, então


\[\begin{align}
f_{\mathbf{x}}(x_1, \ldots, x_p) = \prod\limits_{i=1}^p f(X_i = x_i)
\end{align}\]


a função densidade conjunta fatora nas densidades marginais.










Independência









Exemplo:



Seja \(\Omega = \{1,2,3,4,5,6\}\) com \(P(\{i\}) = 1/6\), para \(i=1,2,3,4,5,6\). Sejam \(A = \{1,2,3,4\}\), \(B = \{4,5,6\}\) e \(C = \{2,3,4\}\).


Mostre que \(A,B\) e \(C\) não são independentes.



 
 
 
 
 
 
 
 










Independência









Exemplo:



Seja \(\Omega = \{1,2,3,4,5,6\}\) com \(P(\{i\}) = 1/6\), para \(i=1,2,3,4,5,6\). Sejam \(A = \{1,2,3,4\}\), \(B = \{4,5,6\}\) e \(C = \{2,3,4\}\).


Mostre que \(A,B\) e \(C\) não são independentes.




Solução:


Temos que \(P(A) = \dfrac{4}{6}\), \(P(B) = \dfrac{3}{6}\) e \(P(C) = \dfrac{3}{6}\). Assim, temos que \[P(A \cap B \cap C) = P(\{4\}) = \dfrac{1}{6}\]


\[\text{e } P(A)P(B)P(C) = \dfrac{4}{6}\dfrac{3}{6}\dfrac{3}{6}= \dfrac{1}{6}\]












Independência









Exemplo:



Seja \(\Omega = \{1,2,3,4,5,6\}\) com \(P(\{i\}) = 1/6\), para \(i=1,2,3,4,5,6\). Sejam \(A = \{1,2,3,4\}\), \(B = \{4,5,6\}\) e \(C = \{2,3,4\}\).


Mostre que \(A,B\) e \(C\) não são independentes.




Solução:


Além disso, temos que \[P(A \cap B) = \dfrac{1}{6},\, P(A \cap C) = \dfrac{2}{6} \text{ e } P(B \cap C) = \dfrac{1}{6},\] entretanto,


\[P(A)P(B) = \dfrac{4}{6}\dfrac{3}{6} = \dfrac{1}{3} \neq \dfrac{1}{6} = P(A \cap B)\]














 
 
 





Estimação por Máxima Verissimilhança









Amostra Aleatória






Seja \(X\) uma variável aleatória (v.a.) com função densidade (caso contínuo) ou função de probabilidade (caso discreto) denotado por \(f(x;\theta) = f_{\theta}(x)\), em que \(\theta\) é o parâmetro desconhecido. Assumiremos que a distribuição de \(X\) pertence a uma certa família \(\mathcal{F} = \{F_{\theta}: \theta \in \Theta \}\) de distribuições indexadas por \(\theta\) e temos que \(\Theta\) é conhecido como espaço paramétrico.









Amostra Aleatória (a.a):



Uma sequência \(X_1, \ldots, X_n\) de \(n\) v.a. independentes e identicamente distribuídas (i.i.d) com função densidade ou função de probabilidade \(f(x;\theta)\), é dito ser amostra aleatória de tamanho \(n\) da distribuição de \(X\).


Como consequência, temos que a densidade conjunta de \(X_1, \ldots, X_n\) é dado por \[\begin{align}
f(x_1, \ldots, x_n; \theta) = \prod\limits_{i=1}^{n} f(x_i; \theta)
\end{align}\]










Estatística









Definição 15:



Qualquer função da amostra \(T = T(X_1, \ldots, X_n)\) que não dependa de parâmetros desconhecidos é chamada de Estatística.






Uma estatística pode ser vista como um método de redução de dados \(X_1, \ldots, X_n\). O objetivo é obter algum resultado que seja resumo dos dados para melhor entendê-los





Exemplos de Estatística:



    

  1. \(\overline{X} = \sum\limits_{i=1}^{n}\dfrac{X_i}{n}\)
    2. 

  2. \(S^2 = \sum\limits_{i=1}^{n}\dfrac{(X_i - \overline{X})^2}{n - 1}\)
    3. 











Modelo Estatístico










Exemplos de Estatística cont.:



    

  1. \(X_{(1)} = \underset{i=1, \ldots, n}{\text{min}}(X_i)\)
    2. 

  2. \(X_{(n)} = \underset{i=1, \ldots, n}{\text{max}}(X_i)\)
    3. 













Definição 16:



Uma estrutura \((\mathcal{X}, \mathcal{A}, \mathcal{F})\) é chamada de modelo estatístico, em que \(\mathcal{X}\) é o conjunto dos possíveis valores de \(X\), \(\mathcal{A}\) é uma \(\sigma\)-álgebra dos subconjuntos de \(X\) e \(\mathcal{F} = \{F_{\theta}:\theta \in \Theta \subset \mathbb{R}^p\}, p = 1,\ldots\) é uma família de distribuições a qual a distribuição de \(X\) pertence.










Estimação Pontual






Seja \((\mathcal{X}, \mathcal{A}, \mathcal{F})\) um modelo estatístico associado a uma variável \(X\), em que a família de distribuições \(\mathcal{F} = \{F_{\theta}:\theta \in \Theta \subset \mathbb{R}^p\}\) depende de um vetor de parâmetros desconhecidos \(\theta\).







Definição 17:



Um estimador pontual para \(\theta\) é uma função \(\delta(X): \mathcal{X} \rightarrow \mathbb{R}\) que assume valores em \(\Theta\).





Um estimador pontual como função apenas da amostra é uma estatística.












Definição 18:



Uma vez observado \(X=x\), temos que \(\delta(x)\) é chamado de estimativa de \(\theta\).






Vamos introduzir o conceito de Máxima Verossimilhança para os casos discretos e contínuos.






Método de Máxima Verossimilhança






Caso Discreto




Suponha que \(X_1, \ldots, X_n\) são variáveis aleatórias (v.a.) discretas com distribuição conjunta discreta e que observamos \(X_1 = x_1, \ldots, X_n = x_n\). Seja,


\[\begin{align}
p_{\theta}(x_1,\ldots, x_n) = P(X_1 = x_1, \ldots, X_n = x_n),
\end{align}\]


considerando o parâmetro \(\theta\) desconhecido.




Seja as observações independentes e \(p_{\theta}(x_i)\) função de probabilidade marginal de \(X_i\), então temos que


\[\begin{align}
p_{\theta}(x_1,\ldots, x_n) = \prod\limits_{i=1}^{n} p_{\theta}(x_i).
\end{align}\]






Método de Máxima Verossimilhança






Caso Contínuo




Suponha que \(X_1, \ldots, X_n\) são v.a. contínuas com distribuição conjunta adotando a densidade conjunta para \(X_1 = x_1, \ldots, X_n = x_n\) dada por,


\[\begin{align}
f_{\theta}(x_1,\ldots, x_n),
\end{align}\]


considerando o parâmetro \(\theta\) desconhecido.




Seja as observações independentes e \(f_{\theta}(x_i)\) função densidade marginal de \(X_i\), então temos que


\[\begin{align}
f_{\theta}(x_1,\ldots, x_n) = \prod\limits_{i=1}^{n} f_{\theta}(x_i).
\end{align}\]






Método de Máxima Verossimilhança









Definição 19:



Dado \({\dot{\mathbf{x}}} = (x_1, \ldots, x_n)^\top\), a função


\[\begin{align}
L(\theta) = L(\theta; {\dot{\mathbf{x}}} ) = f_{\theta}(x_1, \ldots, x_n)
\end{align}\]


observada como função do parâmetro \(\theta\) a ser maximizada é chamada função de máxima verossimilhança.












Definição 20: função de log-verossimilhança



Na maioria das vezes é conveniente trabalhar com o logaritmo da função de verossimilhança


\[\begin{align}
\ell (\theta) = \log \{ L(\theta) \},
\end{align}\]


que é chamada função de log-verossimilhança.










Método de Máxima Verossimilhança






Observação: Se as observações são independentes, então


\[\begin{align}
\ell (\theta) = \log \left\lbrace  \prod\limits_{i=1}^{n} f_{\theta}(x_i) \right\rbrace \quad  \Rightarrow  \quad \ell (\theta) = \sum\limits_{i=1}^{n} \log f_{\theta}(x_i).
\end{align}\]





Definição 21:



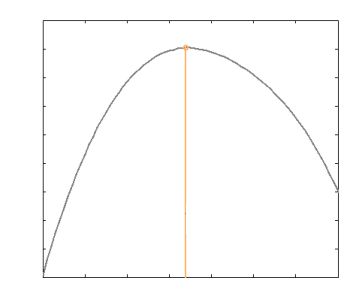
O estimador de máxima Verossimilhança (EMV) de \(\theta\) é o valor \(\hat{\theta} \in \Theta\) que maximiza a função de verossimilhança \(L(\theta)\), sendo \(\Theta\) o espaço paramétrico (conjunto dos possíveis valores de \(\theta\)), ou seja,


\[\begin{align}
\hat{\theta} = \underset{\theta \in \Theta}{\text{arg max }} L(\theta).
\end{align}\]


Dado que a função \(\log(\cdot)\) é estritamente contínua, temos que


\[\begin{align}
\hat{\theta} = \underset{\theta \in \Theta}{\text{arg max }} L(\theta) = \underset{\theta \in \Theta}{\text{arg max }} \ell (\theta).
\end{align}\]








Método de Máxima Verossimilhança






Então, se \(\Theta\) o espaço paramétrico e \(\ell (\theta)\) é diferenciável, o EMV pode ser obtido como raíz da equação




\[\begin{align}
\ell ' (\theta) = \dfrac{\partial \ell \theta}{\partial \theta} \Bigg|_{\theta = \hat{\theta}} = 0
\end{align}\]





Para concluir que a solução anterior é ponto de máximo, é preciso verificar que




\[\begin{align}
\ell '' (\theta) = \dfrac{\partial^2 \ell \theta}{\partial \theta^2} \Bigg|_{\theta = \hat{\theta}} < 0
\end{align}\]








Método de Máxima Verossimilhança









Exemplo (discreto):



Sejam \(X_1, \ldots, X_n\) v.a. independentes e identicamente distribuídas (i.i.d.) com distribuição de Bernoulli, ou seja, \(X_i \sim Bernoulli (p)\), em que \(0 < p < 1\) desconhecido.


Resp.:



 
 
 
 
 
 
 








Método de Máxima Verossimilhança









Exemplo (discreto):



Sejam \(X_1, \ldots, X_n\) v.a. independentes e identicamente distribuídas (i.i.d.) com distribuição de Bernoulli, ou seja, \(X_i \sim Bernoulli (p)\), em que \(0 < p < 1\) desconhecido.




Resp.:


A função de verossimilhança para a Bernoulli é dada por \[L(p) = \prod\limits_{i=1}^{n} p^{x_i} (1-p)^{1-x_i} = p^{\sum\limits_{i=1}^{n}x_i} (1-p)^{n - \sum\limits_{i=1}^{n}x_i}\]


A função de log-verossimilhança é dada por \[\ell(p) = \sum\limits_{i=1}^{n}x_i \log p + (n - \sum\limits_{i=1}^{n}x_i) \log (1-p)\]










Método de Máxima Verossimilhança









Exemplo (discreto):



Sejam \(X_1, \ldots, X_n\) v.a. independentes e identicamente distribuídas (i.i.d.) com distribuição de Bernoulli, ou seja, \(X_i \sim Bernoulli (p)\), em que \(0 < p < 1\) desconhecido.




Resp.:


A derivada de log-verossimilhança em relação a \(p\) é dada por \[\dfrac{d}{dp} \ell(p) = \dfrac{1}{p} \sum\limits_{i=1}^{n}x_i - \dfrac{1}{1-p} \left(n - \sum\limits_{i=1}^{n}x_i \right)\]


Assim, temos que \[\dfrac{d}{dp} \ell(p) \Bigg|_{p = \hat{p}} = \dfrac{1}{\hat{p}} \sum\limits_{i=1}^{n}x_i - \dfrac{1}{1-\hat{p}} \left(n - \sum\limits_{i=1}^{n}x_i \right) = 0\]










Método de Máxima Verossimilhança









Exemplo (discreto):



Sejam \(X_1, \ldots, X_n\) v.a. independentes e identicamente distribuídas (i.i.d.) com distribuição de Bernoulli, ou seja, \(X_i \sim Bernoulli (p)\), em que \(0 < p < 1\) desconhecido.




Resp.:


logo, \[\dfrac{1}{\hat{p}} \sum\limits_{i=1}^{n}x_i = \dfrac{1}{1-\hat{p}} \left(n - \sum\limits_{i=1}^{n}x_i \right) \Rightarrow \hat{p} = \dfrac{1}{n} \sum\limits_{i=1}^{n}X_i = \overline{X}. \]


O estimador de Máxima Verossimilhança (EMV) de \(p\) é dado por \(\hat{p} = \dfrac{1}{n} \sum\limits_{i=1}^{n}X_i = \overline{X}\).










Método de Máxima Verossimilhança





Exemplo:





## Exemplo 1:
set.seed(1)

# Gerando uma amostra Bernoulli
p <- 0.3
x <- rbinom(n = 100, size = 1, prob = p)

# Estimando p
p_hat <- mean(x)
# Visualizando parâmetro estimado
p_hat




[1] 0.32










## Exemplo 2:
set.seed(2)

# Gerando uma amostra Bernoulli
p <- 0.4
x <- rbinom(n = 1000, size = 1, prob = p)

# Estimando p
p_hat <- mean(x)
# Visualizando parâmetro estimado
p_hat




[1] 0.395












Método de Máxima Verossimilhança









Exemplo (contínuo):



 Sejam \(X_1, \ldots, X_n\) v.a. independentes e identicamente distribuídas (i.i.d.) com distribuição \(X_i \sim \mathcal{N}(\mu, 1)\).




Resp.:



 
 
 
 
 
 
 
 










Método de Máxima Verossimilhança









Exemplo (contínuo):



 Sejam \(X_1, \ldots, X_n\) v.a. independentes e identicamente distribuídas (i.i.d.) com distribuição \(X_i \sim \mathcal{N}(\mu, 1)\).




Resp.:


Neste caso, a função de verossimilhança é dado por


\[L(\mu) = \prod\limits_{i=1}^{n} \dfrac{1}{\sqrt{2 \pi}} \exp \left\lbrace -\frac{1}{2} (x_i - \mu)^2 \right\rbrace = (2 \pi)^{-\frac{n}{2}} \exp \left\lbrace -\frac{1}{2} \sum\limits_{i=1}^{n} (x_i - \mu)^2 \right\rbrace,\] em que \(\mu \in \mathbb{R}\). A log-verossimilhança é dado por


\[\ell (\mu) = -\frac{n}{2} \log (2 \pi) - \frac{1}{2} \sum\limits_{i=1}^{n} (x_i - \mu)^2\]










Método de Máxima Verossimilhança









Exemplo (contínuo) cont.:





Resp.:


e temos que


\[\dfrac{d}{d \mu} \ell (\mu) = \sum\limits_{i=1}^{n} (x_i - \mu)\]


logo,


\[\dfrac{d}{d \mu} \ell (\mu) \Bigg|_{\mu = \hat{\mu}} = \sum\limits_{i=1}^{n} (x_i - \hat{\mu}) = 0 \quad \quad \Rightarrow \quad \quad \hat{\mu} = \dfrac{1}{n} \sum\limits_{i=1}^{n}X_i = \overline{X}.\]


Neste caso, temos que


\[\dfrac{d^2}{d \mu^2} \ell (\mu) \Bigg|_{\mu = \hat{\mu}} = -n < 0\]










Método de Máxima Verossimilhança





Exemplo:





## Exemplo 1:
set.seed(1)

# Gerando uma amostra Normal(mu,1)
mu <- 1
x <- rnorm(n = 100, mean = mu, sd = 1)

# Estimando Mu
mu_hat <- mean(x)
# Visualizando parâmetro estimado
mu_hat




[1] 1.108887










## Exemplo 2:
set.seed(2)

# Gerando uma amostra Normal(mu,1)
mu <-6
x <- rnorm(n = 1000, mean = mu, sd = 1)

# Estimando Mu
mu_hat <- mean(x)
# Visualizando parâmetro estimado
mu_hat




[1] 6.061999












Propriedades dos EMV’s



















Teorema 1 (princípio da invariância):



Seja \(g(\cdot)\) uma função real invertível definida em \(\Theta\). Se \(\hat{\theta}\) é o EMV de \(\theta\), então \(g(\hat{\theta})\) é o EMV de \(g(\theta)\).












prova: temos que \(\theta = g^{-1}(g(\theta))\) e, portanto \(L(\theta) = L \left( g^{-1}(g(\theta)) \right)\).


De modo que \(\hat{\theta}\) maximiza os dois lados da equação anterior, isto é \(\hat{\theta} = g^{-1}(\widehat{g(\theta)})\), logo, \(\widehat{g(\theta)} = g(\hat{\theta})\), ou seja, o EMV de \(g(\theta)\) é \(g(\hat{\theta})\).












Propriedades dos EMV’s









Exemplo:



Consideremos novamente \(X_1, \ldots, X_n\) v.a. i.i.d. com distribuição \(Bernoulli(p)\), e suponha que queremos estimar a variância \(g(p) = p(1-p)\).


Vimos que \(\hat{p} = \overline{X}\) é o EMV de \(p\). Logo, pelo princípio da invariância temos que o estimador de \(g(p)\) é


\[g(\hat{p}) = \hat{p}(1-\hat{p}) = \overline{X}(1 - \overline{X}).\]

















Observação: Nos casos em que o suporte da distribuição de \(X\) depende do parâmetro \(\theta\) ou o máximo ocorre na fronteira de \(\Theta\), o EMV não pode ser obtido pelos métodos anteriores. Neste caso, o EMV pode ser obtido inspencionando o gráfico da função de verossimilhança.










Propriedades dos EMV’s





Exemplo:





## Exemplo 1:
set.seed(1)
p <- 0.3
x <- rbinom(n = 100, size = 1, prob = p)
# Estimando p
p_hat <- mean(x)
# Visualizando parâmetro estimado
var(x); p*(1-p)
p_hat*(1-p_hat)




[1] 0.219798
[1] 0.21
[1] 0.2176










## Exemplo 2:
set.seed(2)
p <- 0.4
x <- rbinom(n = 1000, size = 1, prob = p)
# Estimando p
p_hat <- mean(x)
# Visualizando parâmetro estimado
var(x); p*(1-p)
p_hat*(1-p_hat)




[1] 0.2392142
[1] 0.24
[1] 0.238975













Propriedades dos EMV’s


Condições de Regularidade






Muitos resultados sobre EMV’s são obtidos supondo certas condições de regularidade, as quais são listadas a seguir.


Sejam \(n\) observações e \(X_1, \ldots, X_n\) v.a. cuja distribuição comum pertence a uma família de distribuições \(\mathcal{F} = \{F_{\theta}:\theta \in \Theta \}\). Além disso, suponha que:





A0) \(\theta_1 \neq \theta_2 \Rightarrow F_{\theta_1} \neq F_{\theta_2}\)


A1) Todas as distribuições têm o mesmo suporte, o qual não depende do parâmetro \(\theta\) desconhecido.


A2) As observações têm densidade \(f_{\theta} (x) = f(x, \theta)\) com respeito a algum parâmetro \(\theta\), para \(\theta \in \Theta\).


A3) O espaço paramétrico \(\Theta\) contém uma vizinhança do valor verdadeiro de \(\theta\).






Caso Multiparamétrico





 


Vamos considerar agora situações em que \({\boldsymbol \theta} = (\theta_1, \ldots, \theta_p)\) é um vetor paramétrico. Neste caso, \(\Theta \in \mathbb{R}^p\). Nos casos em que as condições de regularidade (A0) - (A3) são satisfeitas em EMV’s de \(\theta_1, \ldots, \theta_p\) são obtidos como soluções das equações





\[\begin{align}
\dfrac{\partial \ell ({\boldsymbol \theta})}{\partial \theta_i} = 0, i = 1, \ldots, p
\end{align}\]






Caso Multiparamétrico




Verossimilhança perfilada


Suponha que a função de verossimilhança depende de dois parâmetros \(\theta_1\) e \(\theta_2\) (ou seja, \({\boldsymbol \theta} = (\theta_1, \theta_2)\)). Então, utilizando a equação


\[\begin{align}
\dfrac{\partial \ell (\theta_1, \theta_2)}{\partial \theta_1} = 0
\end{align}\]


em que substituindo a solução na verossimilhança conjunta, temos agora uma função apenas de \(\theta_2\), ou seja,


\[\begin{align}
g(\theta_2) = \ell (\hat{\theta}_1(\theta_2), \theta_2)
\end{align}\]






Caso Multiparamétrico









Exemplo:



 Sejam \(X_1, \ldots, X_n\) v.a. i.i.d. com distribuição \(N(\mu, \sigma^2)\) em \(\mu\) e \(\sigma^2\) são desconhecidos.


Temos que \({\boldsymbol \theta} = (\mu, \sigma^2)\) e

\[L({\boldsymbol \theta}) = \left(\dfrac{1}{2 \pi \sigma^2}\right)^{\frac{n}{2}} \exp \left\lbrace -\frac{1}{2 \sigma^2} \sum\limits_{i=1}^{n}(x_i - \mu)^2 \right\rbrace\]





Resp.:





 








Caso Multiparamétrico







Exemplo:





## Exemplo 1:
set.seed(1)

# Gerando uma amostra Normal(mu,sigma^2)
mu <- 5
sigma2 <- 2.5
x <- rnorm(n = 100, mean = mu, sd = sqrt(sigma2))

# Estimando Mu e Sigma2
mu_hat <- mean(x)
sigma2_hat <- sum((x - mu_hat)^2) / length(x)

# Visualizando parâmetro estimado
mu_hat
sigma2_hat
var(x)




[1] 5.172166
[1] 1.996736
[1] 2.016905










Vero. para 2 Amostras Indep.






Sejam \(X_1, \ldots, X_n\) e \(Y_1, \ldots, Y_n\) amostras independentes, em que as distribuições conjuntas estão indexadas pelo mesmo parâmetro \(\theta\). Então, a função de verossimilhanda é dada por




\[\begin{align}
L(\theta; {\boldsymbol x}, {\boldsymbol y}) = L(\theta; {\boldsymbol x})L(\theta; {\boldsymbol y})
\end{align}\]




em que \({\boldsymbol x} = (x_1, \ldots, x_n)^\top\) e \({\boldsymbol y} = (y_1, \ldots, y_n)^\top\) são amostras observadas. Assim, a log-verossimilhança é dada por




\[\begin{align}
\ell (\theta; {\boldsymbol x}, {\boldsymbol y}) =  \ell (\theta; {\boldsymbol x}) + \ell (\theta; {\boldsymbol y})
\end{align}\]




A extensão para mais de duas amostras é trivial.






Consistência do EMV










Definição 22:



Seja \(\delta_n\) estimador de \(g(\theta)\) baseado em \(n\) observações. Dizemos que \(\delta_n\) é estimador consistente de \(g(\theta)\) quando \(\forall \epsilon > 0\)


\[\begin{align}
\lim\limits_{n \rightarrow \infty} P(|\delta_n - g(\theta)| > \epsilon) = 0
\end{align}\]


Notação: \(\delta_n \overset{p}{\rightarrow} g(\theta)\) em que \(\overset{p}{\rightarrow}\) denota convergência em probabilidade.


Temos que quando as condições de regularidade forem satisfeitas, o EMV é consistente.










Consistência do EMV










Exemplo:



Sejam \(X_1, \ldots, X_n\) i.i.d. com distribuição \(N(\mu,\sigma^2)\). Vimos que EMV de \(\mu\) é \(\hat{\mu} = \overline{X}\). Pela Lei dos Grandes Números,


\[\overline{X} = \frac{X_1 + \ldots + X_n}{n} \overset{p}{\rightarrow} E(\overline{X})  = \mu\] Logo, \(\hat{\mu} = \overline{X}\) é estimador consistente para \(\mu\).








Consistência do EMV










Exemplo:





## Exemplo 1:
set.seed(55)

# Tamanhos de Amostra
n <- c(10, 30, 50, 100, 1000, 10000)

# Normal(mu,1)
mu <- 5
for (i in n){
  x <- rnorm(n = i, mean = mu, sd = 1)
  # Estimando Mu
  mu_hat <- mean(x)
  # Viés
  vies <- mu_hat - mu
  # Visualizando parâmetro estimado
  print(paste0("Tamanho da Amostra: ", i, ", Mu Estimado:",round(mu_hat,2)," e Viés: ", round(vies,2)))
}




[1] "Tamanho da Amostra: 10, Mu Estimado:4.84 e Viés: -0.16"
[1] "Tamanho da Amostra: 30, Mu Estimado:5.14 e Viés: 0.14"
[1] "Tamanho da Amostra: 50, Mu Estimado:4.94 e Viés: -0.06"
[1] "Tamanho da Amostra: 100, Mu Estimado:4.97 e Viés: -0.03"
[1] "Tamanho da Amostra: 1000, Mu Estimado:5.03 e Viés: 0.03"
[1] "Tamanho da Amostra: 10000, Mu Estimado:4.99 e Viés: -0.01"










Consistência do EMV










Teorema 3:



Sejam \(X_1, \ldots, X_n\) uma a.a. de \(X\) com função densidade (ou probabilidade) \(f(x; \theta)\). Suponha que as condições de regularidade (A0)-(A3) estão satisfeitas e seja \(\theta_0\) o valor verdadeiro de \(\theta\). Então


\[\begin{align}
P_{\theta_0}\left(L(\theta_0)>L(\theta_1)\right) \underset{n \rightarrow \infty}{\rightarrow} 1, \forall \theta_1 \neq \theta_0
\end{align}\]








Consistência do EMV







Exemplo:





## Exemplo 1:
set.seed(5)
# Função de Log-Verossimilhança para uma amostra da Normal
log_likelihood_function <- function(x, mu){
  return(sum(log(dnorm(x, mean = mu, sd = 1))))
}
# Tamanho de Amostra
n <- 1000
# Parâmetro Verdadeiro
mu_0 <- 5
x <- rnorm(n = n, mean = mu_0, sd = 1)
# Verificando o valor da Função de Log-Verossimilhança
mu_1 <- 2; mu_2 <- 5.1; mu_3 <- 4.9
# --
result1 <- log_likelihood_function(x, mu_0); result2 <- log_likelihood_function(x, mu_1)
result3 <- log_likelihood_function(x, mu_2); result4 <- log_likelihood_function(x, mu_3)
#--
print(paste0("Para mu = ", mu_0, ", o valor de l(mu) = :",round(result1,2)))
print(paste0("Para mu = ", mu_1, ", o valor de l(mu) = :",round(result2,2)))
print(paste0("Para mu = ", mu_2, ", o valor de l(mu) = :",round(result3,2)))
print(paste0("Para mu = ", mu_3, ", o valor de l(mu) = :",round(result4,2)))




[1] "Para mu = 5, o valor de l(mu) = :-1430.67"
[1] "Para mu = 2, o valor de l(mu) = :-5982.86"
[1] "Para mu = 5.1, o valor de l(mu) = :-1433.93"
[1] "Para mu = 4.9, o valor de l(mu) = :-1437.41"










Consistência do EMV





Exemplo:









Referências







Básicas


    

  • Bolfarine, H. e Sandoval, M.C. (2001). Introdução à Inferência Estatística, Coleção Matemática Aplicada, Sociedade Brasileira de Matemática.
    • 

  • Casella, G. e Berger, R. (1990) “Statistical Inference”, Wadsworth & Brooks, California
    • 

  • Mood, A. , Graybill, F. e Boes, D. (1974) “Introduction to the Theory of Statistics”, McGraw-Hill, New York.
    • 





Complementar


    

  • Bickel, P.J. e Doksum, K. A. (2001). Mathematical Statistics: Basic Ideas and Selected Topics. San Francisco: Holden Day.
    • 

  • Dudewicz, E.J. e Mishra, S.N. (1988) - Modern Mathematical Statistics - John Wiley & Sons.
    • 

  • Lehmann, E. and Casella, G. (1998) “Theory of Point Estimation”, 2nd edition, Springer, New York.
    • 









 






OBRIGADO!








Slide produzido com quarto