Statistical Machine Learning

Clustering Methods

Prof. Jodavid Ferreira

UFPE

Notation

  • \(X\) or \(Y\)
  • \(x\) or \(y\)
  • \(\mathbf{x}\) or \(\mathbf{y}\)
  • \(\dot{\mathbf{x}}\) or \(\dot{\mathbf{y}}\)
  • \(\mathbf{X}\) or \(\mathbf{Y}\)
  • \(\dot{\mathbf{X}}\) or \(\dot{\mathbf{Y}}\)


    

  • \(p\)
    • 

  • \(n\)
    • 

  • \(i\)
    • 

  • \(j\)
    • 

  • \(K\)
    • 

  • \(k\)
    • 





represent random variables (r.v.);


represent realizations of random variables;


represent random vectors;


represent realizations of random vectors;


represent random matrices;


represent realizations of random matrices;




dimension of features, variables, parameters;


sample size;


\(i\)-th observation, instance (e.g., \(i=1, ..., n\));


\(j\)-th feature, variable, parameter (e.g., \(j=1, ..., p\));


number of classes or clusters;


number of folds in CV / number of nearest neighbors in \(k\)-NN.








The Challenge of



Unsupervised Learning








    

  • Until now, we have been concerned with supervised learning methods such as regression and classification.
    • 





    

  • In the supervised setting, we typically observe:

      

    • An input feature vector \(\dot{\mathbf{x}}_i = (x_{i1}, x_{i2}, \ldots, x_{ip})^\top \in \mathbb{R}^p\) for each observation.
      • 

    • A corresponding response \(y_i \in \mathcal{Y}\).
      • 

    • A training dataset consisting of \(n\) pairs \(\{(\dot{\mathbf{x}}_i, y_i)\}_{i=1}^n\).
      • 

    • 





    

  • The goal is to estimate a function \(f: \mathbb{R}^p \to \mathcal{Y}\) to predict \(Y\) from the features \(\mathbf{x}\).
    • 







The Challenge of



Unsupervised Learning








    

  • Unsupervised learning focuses on settings where we only observe a set of feature vectors \(\dot{\mathbf{x}}_i = (x_{i1}, x_{i2}, \ldots, x_{ip})^\top \in \mathbb{R}^p\) measured on \(n\) observations (\(i = 1, \ldots, n\)).
    • 





    

  • We are not interested in prediction, because we do not observe an associated response variable \(y_i\).
    • 





    

  • Rather, the goal is to discover interesting structure and patterns in the distribution of the feature vectors \(\{\dot{\mathbf{x}}_1, \dots, \dot{\mathbf{x}}_n\}\).
    • 







The Challenge of



Unsupervised Learning








    

  • Key questions in Unsupervised Learning:

      

    • Is there an informative way to visualize the data?
      • 

    • Can we discover subgroups among the variables or among the observations?
      • 

    • 





    

  • Unsupervised learning refers to a diverse set of techniques for answering questions such as these.
    • 





    

  • This chapter will focus on two particular types:

      

    • Clustering: Discovering unknown subgroups in data.
      • 

    • Principal Components Analysis (PCA): Data visualization or pre-processing.
      • 

    • 








What is Clustering?







    

  • Clustering refers to a very broad set of techniques for finding subgroups, or clusters, in a data set.
    • 





    

  • When we cluster the observations of a data set, we seek to partition them into distinct groups so that:

      

    • Observations within each group are quite similar to each other.
      • 

    • Observations in different groups are quite different from each other.
      • 

    • 





    

  • The definition of “similar” or “different” is often a domain-specific consideration based on knowledge of the data.
    • 







Clustering vs. PCA










    

  • Both clustering and Principal Component Analysis (PCA) seek to simplify the data via a small number of summaries.
    • 






    

  • However, their mechanisms are different:

      

    • PCA looks to find a low-dimensional representation of the observations that explain a good fraction of the variance.
      • 

    • Clustering looks to find homogeneous subgroups among the observations.
      • 

    • 







Applications of Clustering







    

  • Biology / Medicine:

      

    • Identifying unknown subtypes of breast cancer from tissue samples with gene expression measurements.
      • 

    • Discovering structure (distinct clusters) in a data set without prior labels.
      • 

    • 






    

  • Marketing:

      

    • Performing market segmentation by identifying subgroups of people who might be more receptive to a particular form of advertising or more likely to purchase a product.
      • 

    • 







K-Means Clustering



Introduction








    

  • K-Means clustering is a simple and elegant approach for partitioning a data set into \(K\) distinct, non-overlapping clusters.
    • 






    

  • To perform K-Means clustering, we must first specify the desired number of clusters \(K\).
    • 






    

  • The K-Means algorithm then assigns each observation to exactly one of the \(K\) clusters.
    • 







K-Means Clustering



Objective Function





    

  • Let \(C_1, \ldots, C_K\) denote sets containing the indices of the observations in each cluster.
    • 

  • These sets satisfy two properties:

      

    1. \(C_1 \cup C_2 \cup \dots \cup C_K = \{1, \ldots, n\}\). Each observation belongs to at least one cluster.
      2. 

    2. \(C_k \cap C_{k'} = \emptyset\) for all \(k \neq k'\). Clusters are non-overlapping.
      3. 

    • 

  • The idea behind K-Means clustering is that a good clustering is one for which the within-cluster variation is as small as possible.
    • 

  • We want to solve the problem: \[ \min_{C_1, \ldots, C_K} \sum_{k=1}^K W(C_k) \] where \(W(C_k)\) is a measure of the amount by which observations within cluster \(C_k\) differ from each other.
    • 







K-Means Clustering



Within-Cluster Variation








    

  • The most common choice for within-cluster variation is based on squared Euclidean distance: \[ W(C_k) = \frac{1}{|C_k|} \sum_{i,i' \in C_k} \sum_{j=1}^p (x_{ij} - x_{i'j})^2 = \frac{1}{|C_k|} \sum_{i,i' \in C_k} \|\dot{\mathbf{x}}_i - \dot{\mathbf{x}}_{i'}\|_2^2 \] where \(|C_k|\) denotes the number of observations in the \(k\)-th cluster.
    • 






    

  • This formula represents the sum of all pairwise squared Euclidean distances between observations in the \(k\)-th cluster, divided by the total number of observations in that cluster.
    • 







K-Means Clustering



Centroid vs. Pairwise Distance Equivalence








    

  • The equivalence between the pairwise distances within a cluster and the distance to the cluster centroid is a key algebraic property of squared Euclidean distance: \[ \frac{1}{|C_k|} \sum_{i,i' \in C_k} \|\dot{\mathbf{x}}_i - \dot{\mathbf{x}}_{i'}\|^2_2 = 2 \sum_{i \in C_k} \|\dot{\mathbf{x}}_i - \dot{\bar{\mathbf{x}}}_k\|^2_2 \] where \(\dot{\bar{\mathbf{x}}}_k = \frac{1}{|C_k|} \sum_{i \in C_k} \dot{\mathbf{x}}_i\) is the cluster centroid.
    • 







K-Means Clustering



Centroid vs. Pairwise Distance Equivalence









Proof: - Expanding the left-hand side: \[ \sum_{i,i' \in C_k} \|\dot{\mathbf{x}}_i - \dot{\mathbf{x}}_{i'}\|^2_2 = \sum_{i,i' \in C_k} \left( \|\dot{\mathbf{x}}_i\|^2_2  - 2 \dot{\mathbf{x}}_i^\top \dot{\mathbf{x}}_{i'} + \|\dot{\mathbf{x}}_{i'}\|^2_2 \right) \] \[ = |C_k| \sum_{i \in C_k} \|\dot{\mathbf{x}}_i\|^2_2 - 2 \left( \sum_{i \in C_k} \dot{\mathbf{x}}_i \right)^\top \left( \sum_{i' \in C_k} \dot{\mathbf{x}}_{i'} \right) + |C_k| \sum_{i' \in C_k} \|\dot{\mathbf{x}}_{i'}\|^2_2 \] \[ = 2 |C_k| \sum_{i \in C_k} \|\dot{\mathbf{x}}_i\|^2_2 - 2 \left( |C_k| \dot{\bar{\mathbf{x}}}_k \right)^\top \left( |C_k| \dot{\bar{\mathbf{x}}}_k \right) = 2 |C_k| \sum_{i \in C_k} \|\dot{\mathbf{x}}_i\|^2_2 - 2 |C_k|^2 \|\dot{\bar{\mathbf{x}}}_k\|^2_2 \] - Expanding the right-hand side (centroid-based distance sum multiplied by \(2|C_k|\)): \[ 2 |C_k| \sum_{i \in C_k} \|\dot{\mathbf{x}}_i - \dot{\bar{\mathbf{x}}}_k\|^2_2 = 2 |C_k| \sum_{i \in C_k} \left( \|\dot{\mathbf{x}}_i\|^2_2 - 2\dot{\mathbf{x}}_i^\top \dot{\bar{\mathbf{x}}}_k + \|\dot{\bar{\mathbf{x}}}_k\|^2_2 \right) \] \[ = 2 |C_k| \left( \sum_{i \in C_k} \|\dot{\mathbf{x}}_i\|^2_2 - 2 \dot{\bar{\mathbf{x}}}_k^\top (|C_k| \dot{\bar{\mathbf{x}}}_k) + |C_k| \|\dot{\bar{\mathbf{x}}}_k\|^2_2 \right) = 2 |C_k| \sum_{i \in C_k} \|\dot{\mathbf{x}}_i\|^2_2 - 2 |C_k|^2 \|\dot{\bar{\mathbf{x}}}_k\|^2_2 \]










K-Means Clustering



Optimization Problem





    

  • Combining the objective function with the definition of within-cluster variation, the K-Means optimization problem is: \[ \min_{C_1, \ldots, C_K} \sum_{k=1}^K \frac{1}{|C_k|} \sum_{i,i' \in C_k} \|\dot{\mathbf{x}}_i - \dot{\mathbf{x}}_{i'}\|_2^2 = \min_{C_1, \ldots, C_K} 2 \sum_{k=1}^K \sum_{i \in C_k} \|\dot{\mathbf{x}}_i - \dot{\bar{\mathbf{x}}}_k\|_2^2 \]
    • 

  • Alternatively, this can be formulated as a joint minimization over cluster assignments \(C_1, \dots, C_K\) and representative centroids \(\boldsymbol{\mu}_1, \dots, \boldsymbol{\mu}_K \in \mathbb{R}^p\): \[ \min_{C_1, \ldots, C_K, \boldsymbol{\mu}_1, \dots, \boldsymbol{\mu}_K} \sum_{k=1}^K \sum_{i \in C_k} \|\dot{\mathbf{x}}_i - \boldsymbol{\mu}_k\|_2^2 \] which shows that the optimal representative centroids are indeed the sample means (centroids) of each cluster.
    • 







The K-Means Algorithm



Steps





    

  • A simple iterative algorithm is used to find a local optimum for the K-Means optimization problem.
    • 





    

  1. Random Assignment: Randomly assign a number, from 1 to \(K\), to each of the observations. These serve as initial cluster assignments.
    2. 

  2. Iterate until cluster assignments stop changing:
    

      

    1. Compute Centroids: For each of the \(K\) clusters, compute the cluster centroid. The \(k\)-th cluster centroid is the vector of the \(p\) feature means for the observations in the \(k\)-th cluster. \[ \dot{\bar{x}}_{kj} = \frac{1}{|C_k|} \sum_{i \in C_k} x_{ij} \]
      2. 

    2. Assign Observations: Assign each observation to the cluster whose centroid is closest (using Euclidean distance).
      3. 

    3. 









The K-Means Algorithm



Why it Works








    

  • The algorithm is guaranteed to decrease the value of the objective function at each step.
    • 

  • The identity \(\frac{1}{|C_k|} \sum_{i,i' \in C_k} \sum_{j=1}^p (x_{ij} - x_{i'j})^2 = 2 \sum_{i \in C_k} \sum_{j=1}^p (x_{ij} - \dot{\bar{x}}_{kj})^2\) is illuminating.

      

    • Step 2(a) computes cluster means that minimize the sum of squared deviations for fixed assignments.
      • 

    • Step 2(b) reallocates observations, which can only improve the objective for fixed centroids.
      • 

    • 

  • The algorithm stops when the cluster assignments no longer change, indicating a local optimum has been reached.
    • 







The K-Means Algorithm



Multiple Runs








    

  • Since the K-Means algorithm finds a local rather than a global optimum, the results depend on the initial (random) cluster assignment.
    • 






    

  • Therefore, it is important to run the algorithm multiple times from different random initial configurations.
    • 






    

  • Then, one selects the best solution, i.e., the one for which the objective function is smallest.
    • 








K-Means Visualization



Initial Data and Progression








    

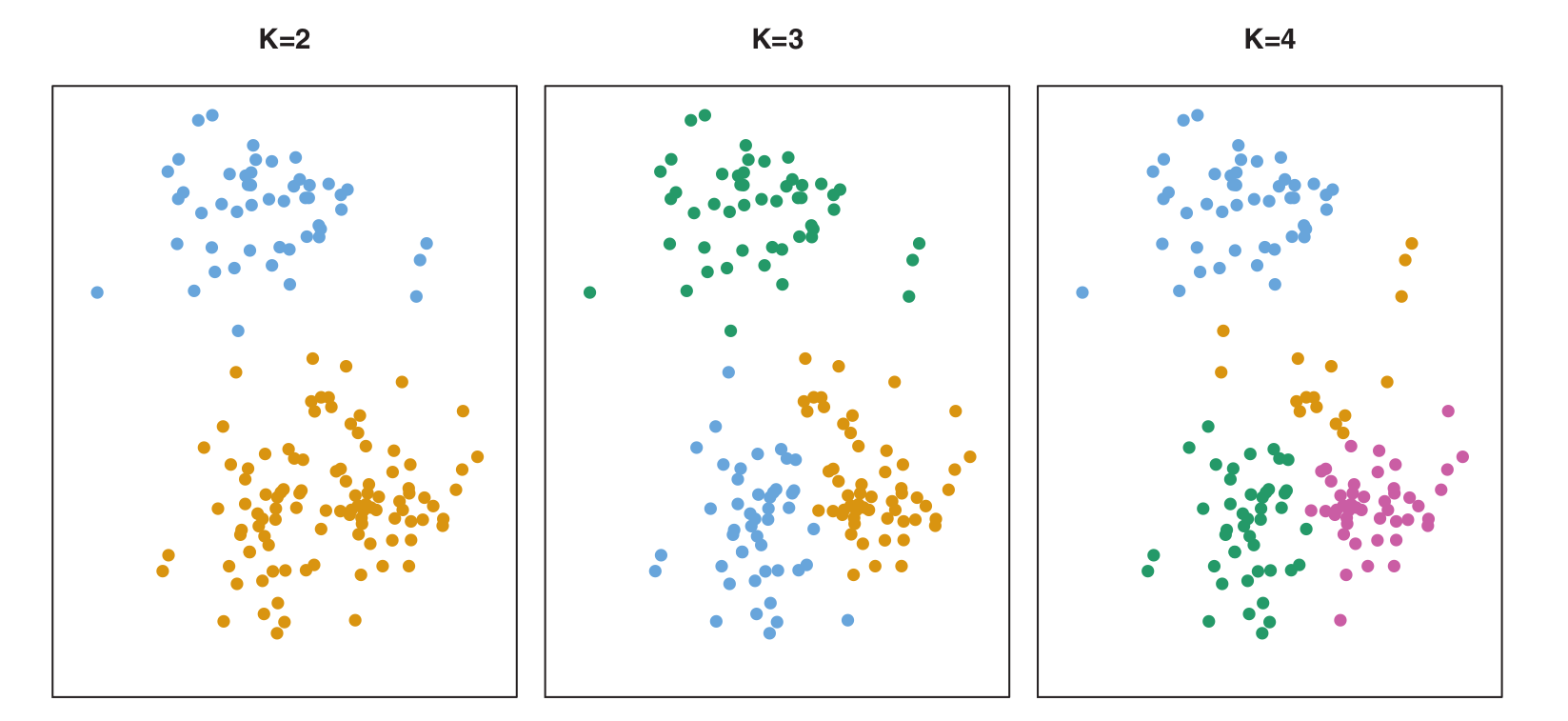
  • Let’s visualize the K-Means algorithm with a simulated 2D dataset (\(n=150\)).
    • 










 Figure (K=2, K=3, K=4): Shows how the clusters are formed for different values of \(K\).




Scatter plots showing 150 points in 2D space, colored by K-means cluster assignment for K=2, K=3, and K=4. The K=3 plot shows three distinct clusters.










K-Means Visualization



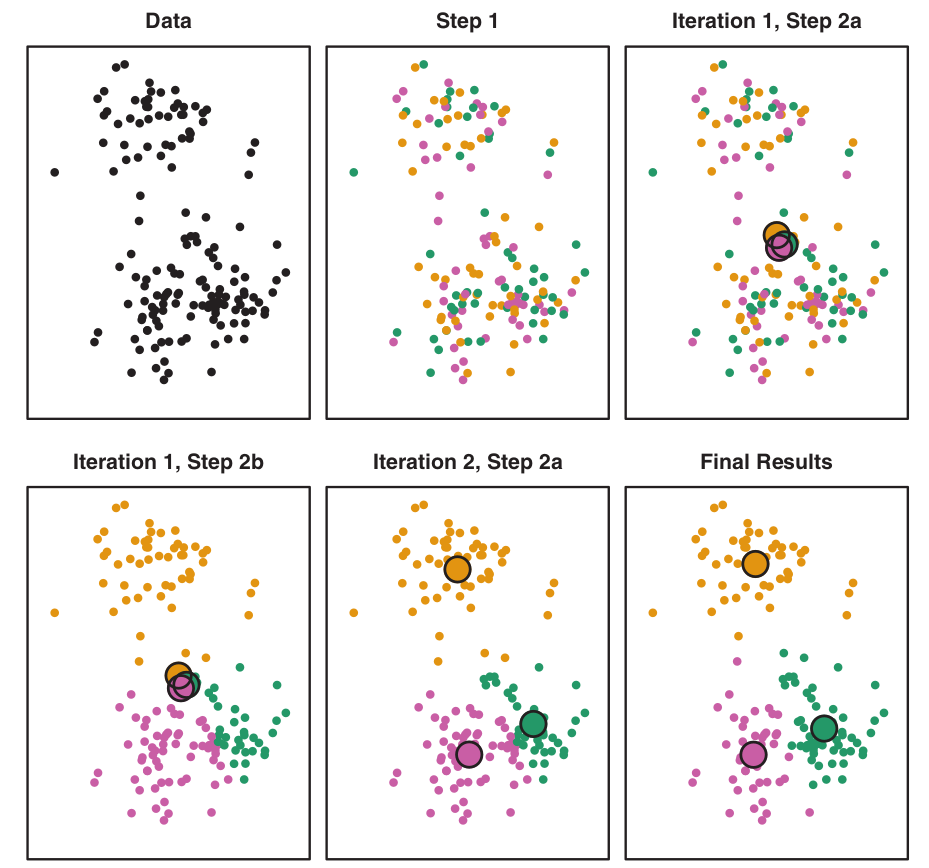
Algorithm Steps (K=3)










 Figure: Illustrates the progression of K-Means algorithm for \(K=3\):


    

  • Top left: Observations.
    • 

  • Top center: Initial random assignment.
    • 

  • Top right: Centroids computed.
    • 

  • Bottom left: Observations reassigned.
    • 

  • Bottom center: New centroids.
    • 

  • Bottom right: Final result after 10 iterations.
    • 





Sequence of 6 panels showing the K-means algorithm's progression. From initial data and random assignment to final clustered result after multiple iterations, with centroids marked by large disks.








K-Means Visualization



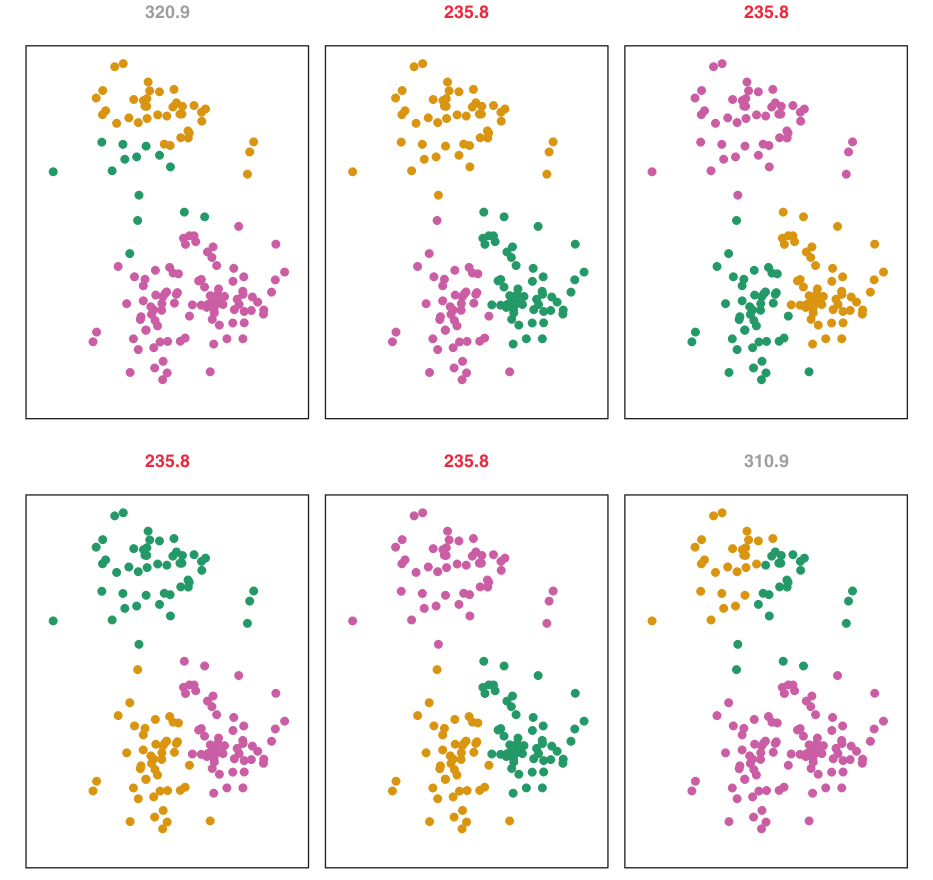
Multiple Initializations












Figure: K-Means clustering performed six times with different random initial assignments for \(K=3\).


    

  • Values above each plot show the objective function.
    • 

  • Multiple local optima are obtained. The best solution (lowest objective, \(235.8\)) provides better separation.
    • 





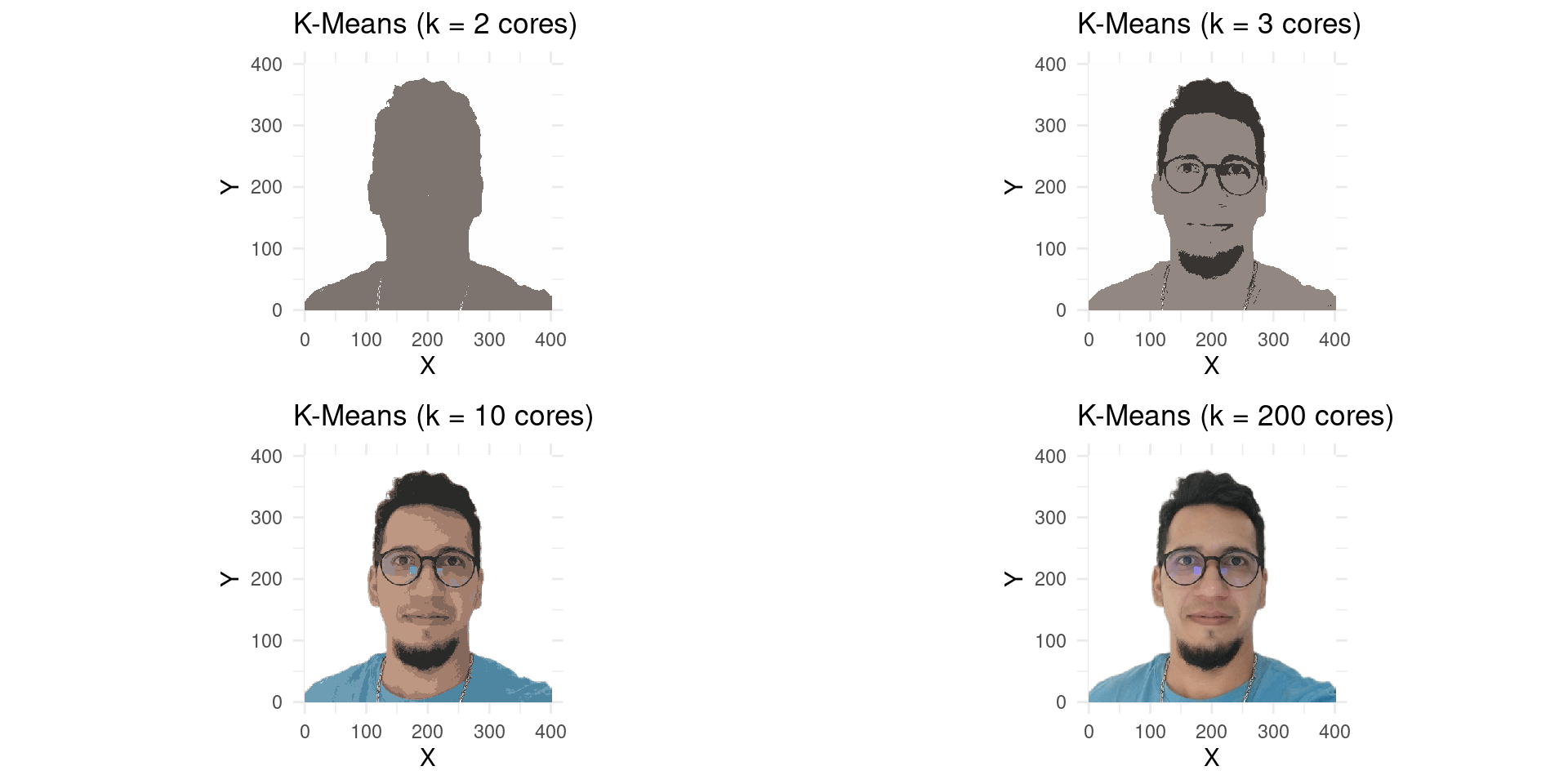
Six scatter plots showing K-means clustering results for K=3 from different random initializations. The objective function value is shown above each plot, highlighting different local optima.








R Example: K-Means on Image Pixels



Goal








    

  • We will use K-Means to cluster the pixels of an image based on their colors (R, G, B values).
    • 






    

  • Each pixel will then be represented by its cluster’s centroid.
    • 






    

  • The number of clusters (\(K\)) will correspond to the number of colors in the resulting image.
    • 







R Example: K-Means on Image Pixels



Code - Data Preparation










library(jpeg) # For reading JPEG images
library(tibble) # For creating data frames
library(dplyr) # For data manipulation
library(ggplot2) # For plotting

# Create a dummy image for demonstration if actual image is not present
# In a real scenario, you'd replace this with your actual image path
if (!file.exists("images/JODAVID.jpg")) {
  message("images/JODAVID.jpg not found. Creating a dummy image for demonstration.")
  # Create a simple image data (e.g., 50x50, 3 channels)
  dummy_image_data <- array(runif(50*50*3), dim = c(50, 50, 3))
  # Create the directory if it doesn't exist
  if (!dir.exists("Figures")) {
    dir.create("Figures")
  }
  # Save a simple JPEG image
  writeJPEG(dummy_image_data, "images/JODAVID.jpg")
}


# Read the image
imagem <- readJPEG("images/JODAVID.jpg")

# Organize the image into a data frame (long format)
# Each row represents a pixel with its (X,Y) coordinates and RGB values
imagemRGB <- tibble(
  X = rep(1:dim(imagem)[2], each = dim(imagem)[1]),
  Y = rep(dim(imagem)[1]:1, dim(imagem)[2]), # Y-axis inverted for plotting
  R = as.vector(imagem[,,1]),
  G = as.vector(imagem[,,2]),
  B = as.vector(imagem[,,3])
)








R Example: K-Means on Image Pixels



Code - Data Preparation













R Example: K-Means on Image Pixels



Code - K-Means Application










# Specify the number of clusters (colors)
k <- 2

# Apply K-Means clustering
# We cluster the RGB values, ignoring X and Y coordinates for clustering logic
kMeans_result_k2 <- kmeans(imagemRGB[, c("R", "G", "B")], centers = k)

# Add the cluster assignment and new color (centroid color) to the data frame
imagemRGB_k2 <- imagemRGB |> 
  mutate(cluster = kMeans_result_k2$cluster) |> 
  mutate(kColours = rgb(
    kMeans_result_k2$centers[cluster, "R"],
    kMeans_result_k2$centers[cluster, "G"],
    kMeans_result_k2$centers[cluster, "B"]
  ))

# Plot the image with k=2 colors
p1 <- ggplot(imagemRGB_k2, aes(x = X, y = Y, color = I(kColours))) +
  geom_point(show.legend = FALSE, shape = 15, size = 0.1) + # Use shape 15 for square pixels
  labs(title = paste("K-Means (k =", k, "cores)")) +
  theme_minimal() +
  theme(aspect.ratio = dim(imagem)[1]/dim(imagem)[2]) + # Maintain aspect ratio
  scale_color_identity() # Use exact colors from kColours








R Example: K-Means on Image Pixels



K-Means with K=2 Colors













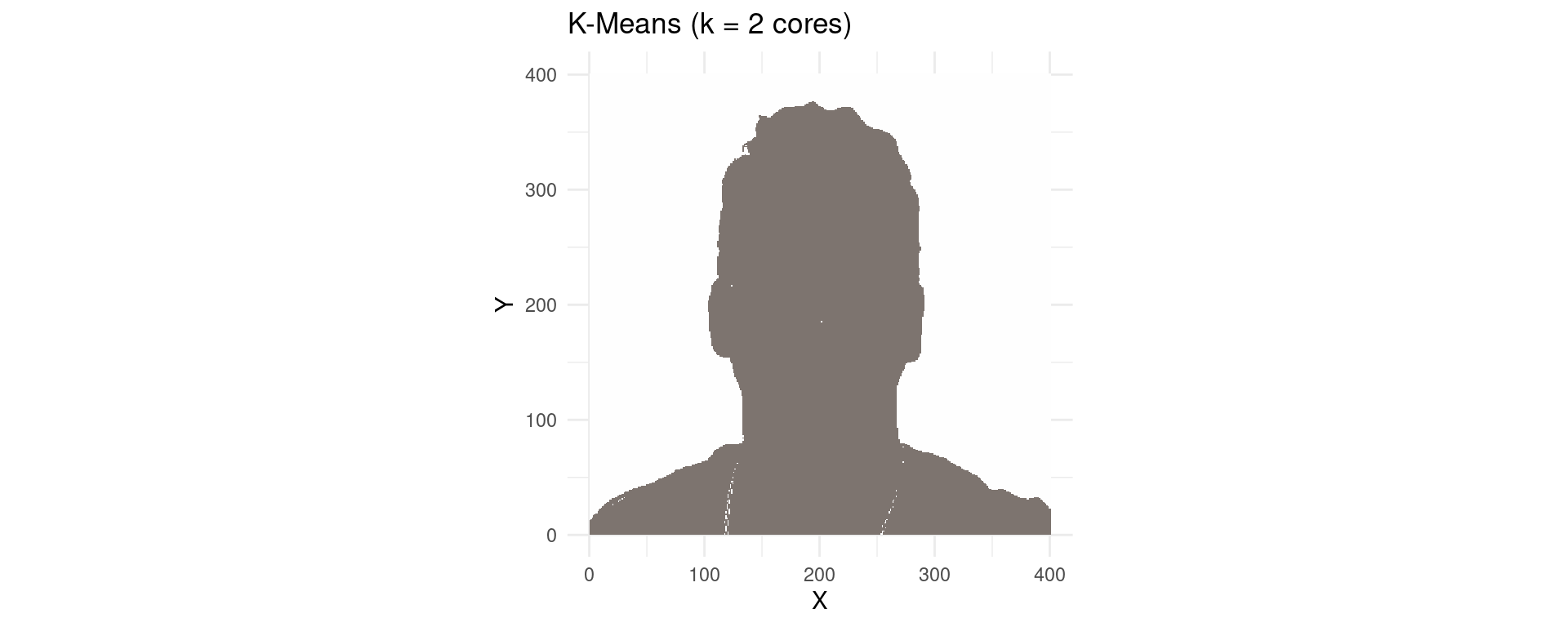
R Example: K-Means on Image Pixels



More Colors!








    

  • Let’s try with more colors, say \(K=3\), \(K=10\), and \(K=200\).
    • 





# For k=3
k <- 3
kMeans_result_k3 <- kmeans(imagemRGB[, c("R", "G", "B")], centers = k)
imagemRGB_k3 <- imagemRGB |> 
  mutate(cluster = kMeans_result_k3$cluster) |> 
  mutate(kColours = rgb(
    kMeans_result_k3$centers[cluster, "R"],
    kMeans_result_k3$centers[cluster, "G"],
    kMeans_result_k3$centers[cluster, "B"]
  ))

# Plot for k=3
p2 <- ggplot(imagemRGB_k3, aes(x = X, y = Y, color = I(kColours))) +
  geom_point(show.legend = FALSE, shape = 15, size = 0.1) +
  labs(title = paste("K-Means (k =", k, "cores)")) +
  theme_minimal() + theme(aspect.ratio = dim(imagem)[1]/dim(imagem)[2]) + scale_color_identity()









R Example: K-Means on Image Pixels



K-Means with K=10 Colors










k <- 10
kMeans_result_k10 <- kmeans(imagemRGB[, c("R", "G", "B")], centers = k)
imagemRGB_k10 <- imagemRGB |> 
  mutate(cluster = kMeans_result_k10$cluster) |> 
  mutate(kColours = rgb(
    kMeans_result_k10$centers[cluster, "R"],
    kMeans_result_k10$centers[cluster, "G"],
    kMeans_result_k10$centers[cluster, "B"]
  ))

p3 <- ggplot(imagemRGB_k10, aes(x = X, y = Y, color = I(kColours))) +
  geom_point(show.legend = FALSE, shape = 15, size = 0.1) +
  labs(title = paste("K-Means (k =", k, "cores)")) +
  theme_minimal() + theme(aspect.ratio = dim(imagem)[1]/dim(imagem)[2]) + scale_color_identity()








R Example: K-Means on Image Pixels



K-Means with K=200 Colors










k <- 200
kMeans_result_k200 <- kmeans(imagemRGB[, c("R", "G", "B")], centers = k)
imagemRGB_k200 <- imagemRGB |> 
  mutate(cluster = kMeans_result_k200$cluster) |> 
  mutate(kColours = rgb(
    kMeans_result_k200$centers[cluster, "R"],
    kMeans_result_k200$centers[cluster, "G"],
    kMeans_result_k200$centers[cluster, "B"]
  ))

p4 <- ggplot(imagemRGB_k200, aes(x = X, y = Y, color = I(kColours))) +
  geom_point(show.legend = FALSE, shape = 15, size = 0.1) +
  labs(title = paste("K-Means (k =", k, "cores)")) +
  theme_minimal() + theme(aspect.ratio = dim(imagem)[1]/dim(imagem)[2]) + scale_color_identity()








R Example: K-Means on Image Pixels



K-Means with differents Colors













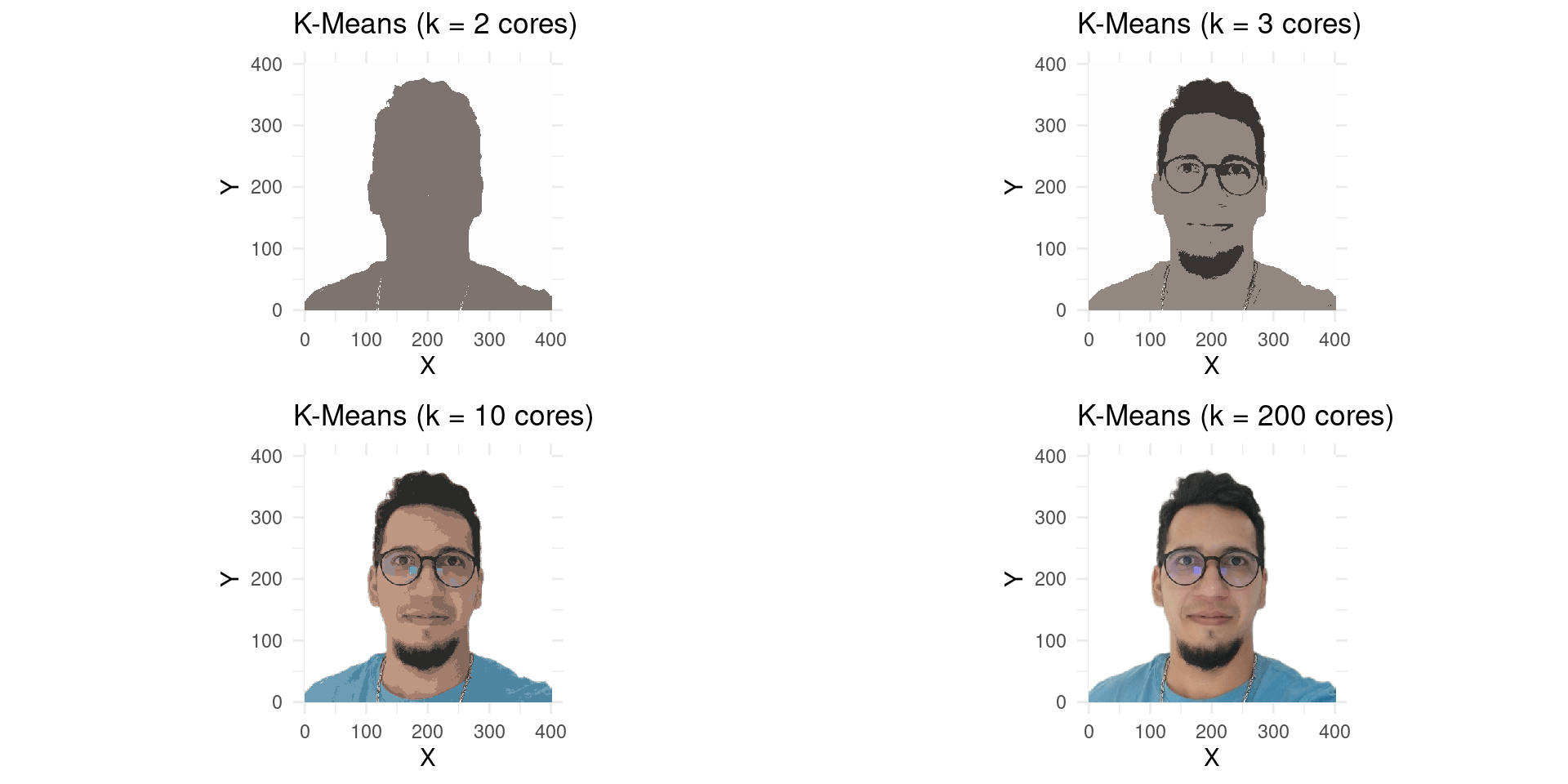
The Elbow Method


Defining the Optimal K








The Elbow method is a popular heuristic to help determine the optimal number of clusters (\(K\)) for the K-Means algorithm.


How it Works:


    

  • It calculates the Within-Cluster Sum of Squares (WSS) for different values of \(K\) (e.g., from 1 to 10 or more).
    • 

  • WSS measures the compactness of each cluster; the lower the WSS, the more compact the clusters.
    • 

  • It then plots the WSS against \(K\).
    • 





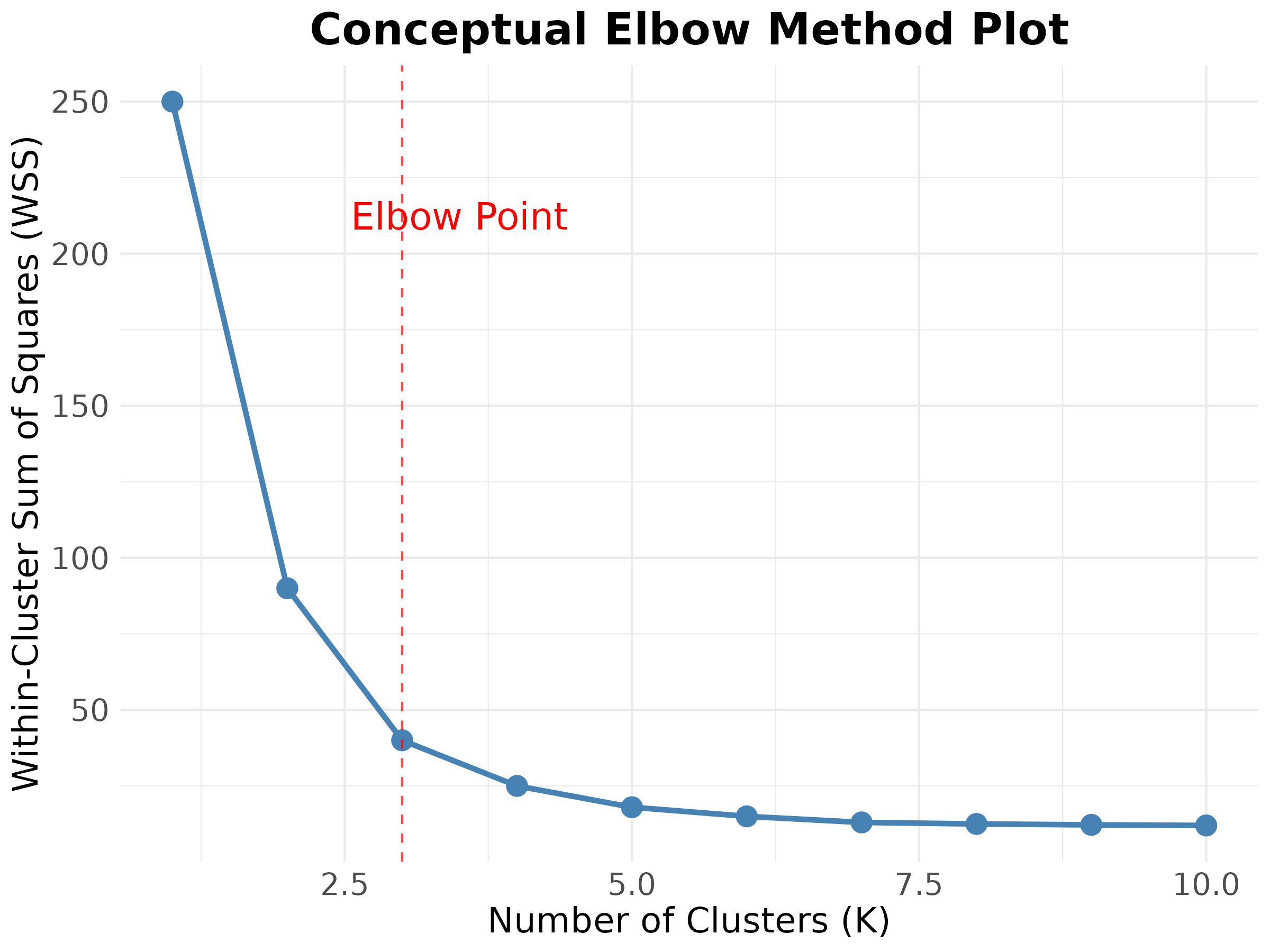
Graph of the Elbow method showing Within-Cluster Sum of Squares (WSS) on the Y-axis versus the number of clusters (K) on the X-axis. The WSS curve decreases rapidly and then flattens, forming an 'elbow' around K=3 or K=4, which is the suggested point.








The Elbow Method


Defining the Optimal K








Identifying the Ideal \(K\):


    

  • As \(K\) increases, the WSS will always decrease (more clusters mean less dispersion within each).
    • 

  • One looks for the point on the curve where the rate of decrease in WSS sharply changes and starts to ‘flatten out’ – this is the ‘elbow’.
    • 

  • This point suggests that adding more clusters beyond this point does not provide a significant gain in the overall compactness of the clusters.
    • 



Considerations:




Graph of the Elbow method showing Within-Cluster Sum of Squares (WSS) on the Y-axis versus the number of clusters (K) on the X-axis. The WSS curve decreases rapidly and then flattens, forming an 'elbow' around K=3 or K=4, which is the suggested point.


    

  • It is a visual and subjective approach.
    • 

  • A clear “elbow” may not always be apparent.
    • 









Example: Elbow Method


Practical Application - Jodavid Image











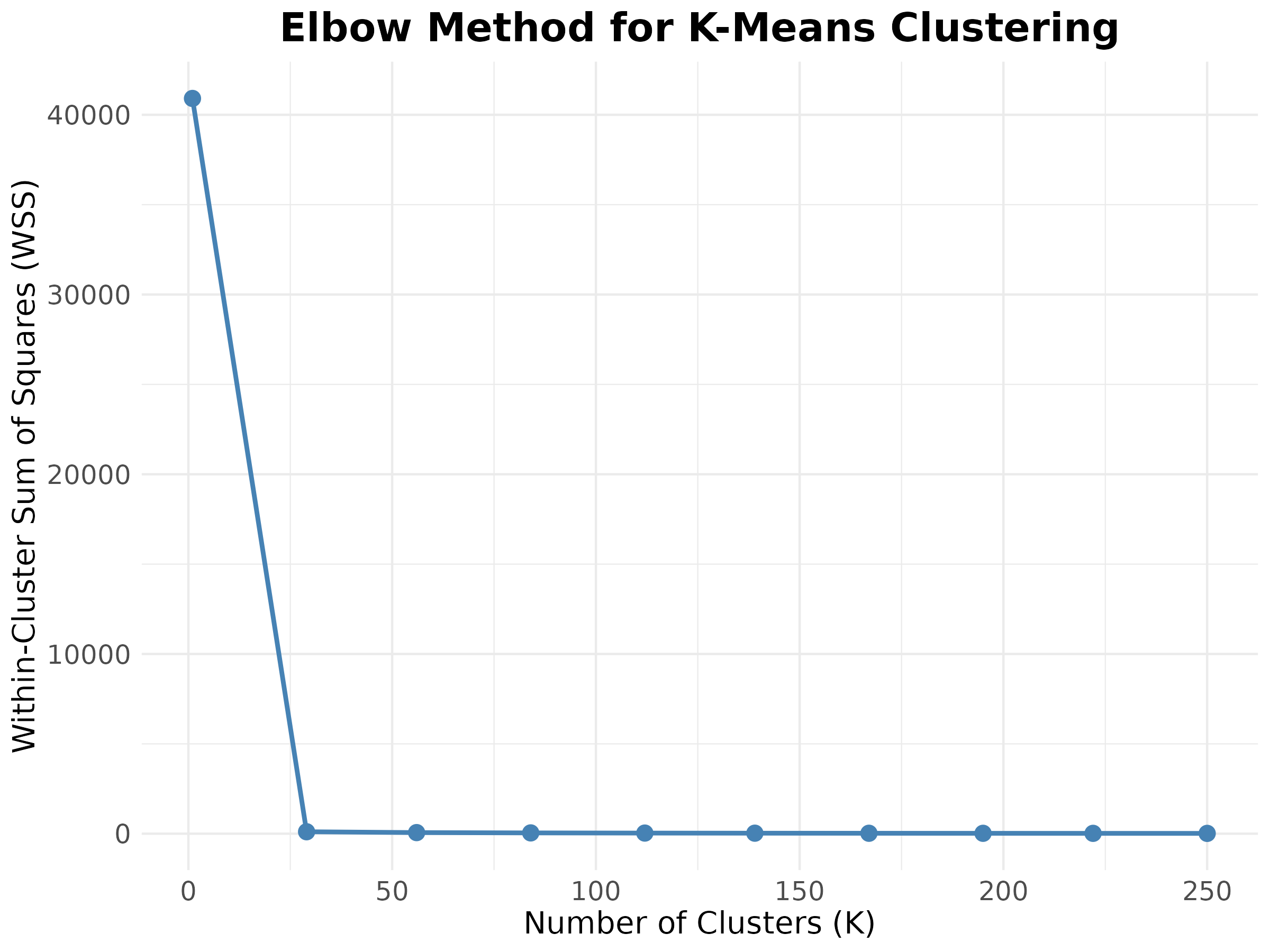
Example: Elbow Method


Practical Application - Jodavid Image









Hierarchical Clustering



Introduction








    

  • One potential disadvantage of K-Means clustering is that it requires us to pre-specify the number of clusters K.
    • 






    

  • Hierarchical clustering is an alternative approach which does not require that we commit to a particular choice of K.
    • 






    

  • It results in an attractive tree-based representation of the observations, called a dendrogram.
    • 







Hierarchical Clustering



Agglomerative Approach








    

  • This section describes bottom-up or agglomerative clustering.
    • 






    

  • This is the most common type of hierarchical clustering.
    • 






    

  • A dendrogram is generally depicted as an upside-down tree, built starting from the leaves and combining clusters up to the trunk.
    • 







Interpreting a Dendrogram



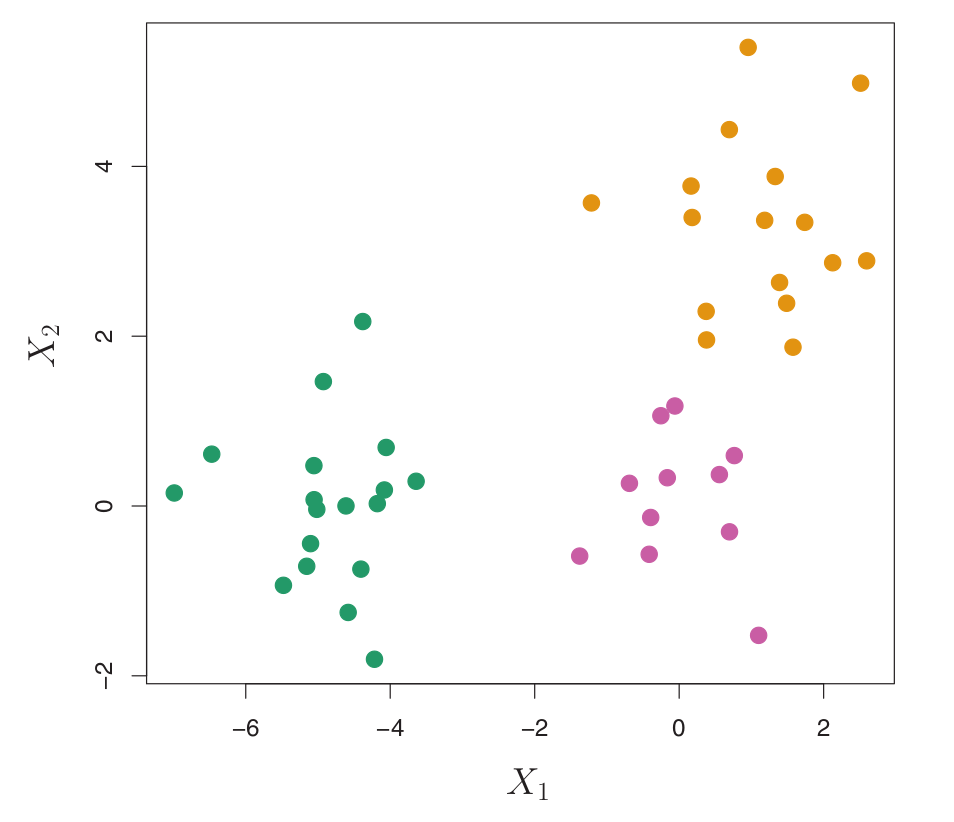
Example Data





    

  • Consider a simulated data set with 45 observations in 2D space, generated from a three-class model.
    • 

  • The true class labels are shown in different colors, but we will treat them as unknown for clustering.
    • 










 Figure:


    

  • 45 observations in 2D space.
    • 

  • Three distinct classes, shown in separate colors.
    • 

  • We will seek to cluster the observations to discover these classes.
    • 





Scatter plot of 45 observations in 2D space, colored by their true (hidden) class. Three distinct clusters are visible.










Interpreting a Dendrogram



Fusions and Similarity








    

  • In a dendrogram:

      

    • Each leaf represents one observation.
      • 

    • As we move up the tree, leaves fuse into branches. These fusions correspond to observations that are similar to each other.
      • 

    • The earlier (lower in the tree) fusions occur, the more similar the groups of observations are to each other.
      • 

    • Observations that fuse later (near the top of the tree) tend to be quite different.
      • 

    • 





    

  • The height of this fusion (measured on the vertical axis) indicates how different the two observations/clusters are.
    • 







Interpreting a Dendrogram



Important Caution








    

  • It is important to understand that the proximity of observations along the horizontal axis in a dendrogram does NOT imply similarity.
    • 






    

  • For any two observations, similarity is determined by the height on the vertical axis where the branches containing those two observations first fuse.
    • 






    

  • A dendrogram can be reordered horizontally without changing its meaning, as long as the vertical fusion heights are preserved.
    • 







Interpreting a Dendrogram



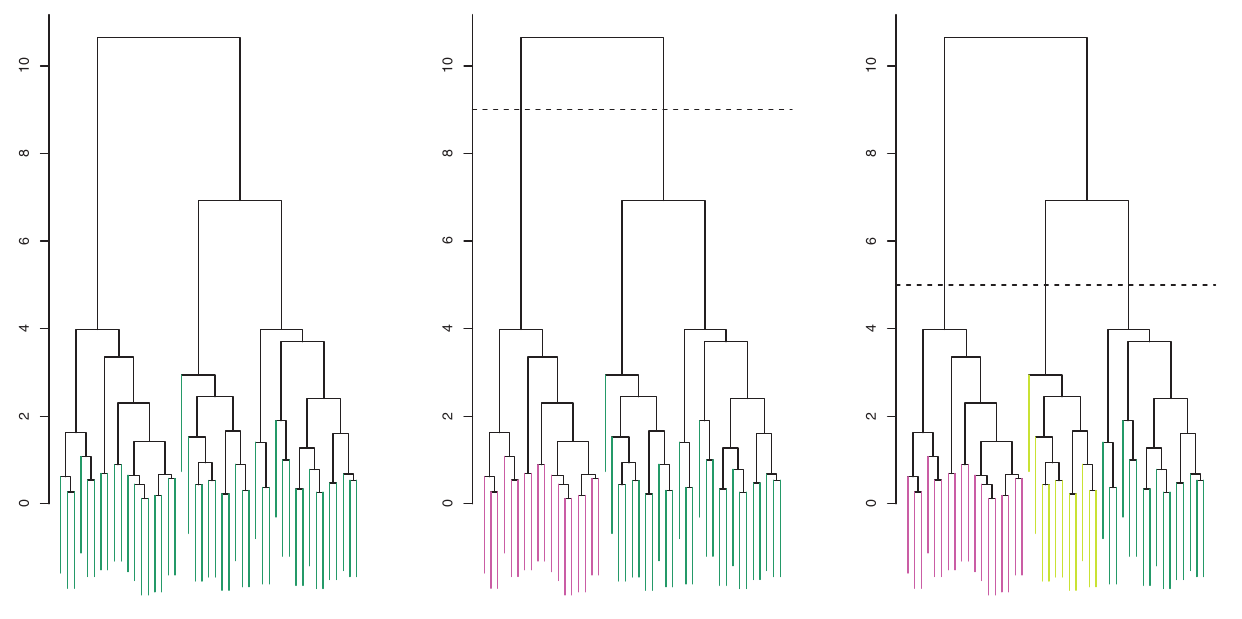
Identifying Clusters





    

  • To identify clusters from a dendrogram, we make a horizontal cut across the tree.
    • 

  • The distinct sets of observations beneath the cut can be interpreted as clusters.
    • 

  • The height of the cut serves the same role as \(K\) in K-Means clustering: it controls the number of clusters obtained.
    • 












Figure:


    

  • Left: Dendrogram.
    • 

  • Center: Cut at height 9, yielding two clusters.
    • 

  • Right: Cut at height 5, yielding three clusters.

      

    • Colors are for display, not used in clustering.
      • 

    • 





Three dendrograms. Left: the full dendrogram. Center: the dendrogram cut at height 9, showing two clusters. Right: the dendrogram cut at height 5, showing three clusters.










Interpreting a Dendrogram



Identifying Clusters





Three dendrograms. Left: the full dendrogram. Center: the dendrogram cut at height 9, showing two clusters. Right: the dendrogram cut at height 5, showing three clusters.




Interpreting a Dendrogram



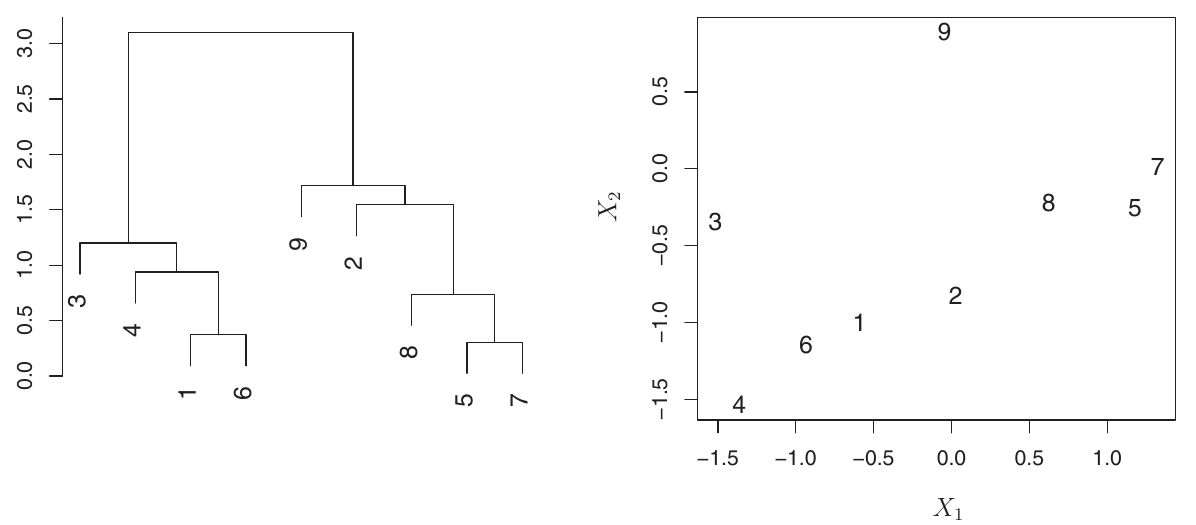
Horizontal Axis Caution Example





    

  • Consider this dendrogram for 9 observations.
    • 

  • Observations 5 and 7 are very similar (fuse low). Observations 1 and 6 are also similar.
    • 

  • However, observations 9 and 2 are not necessarily similar just because they appear close horizontally. Their fusion height is higher.
    • 










 Figure:


    

  • Left: Dendrogram with 9 observations.
    • 

  • Right: Raw data for these 9 observations.
    • 

  • Confirms that horizontal proximity is misleading; vertical fusion height determines similarity.
    • 





Left: A dendrogram for 9 observations. Right: A scatter plot of the 9 observations in 2D space. Used to illustrate that horizontal proximity in dendrograms is not a measure of similarity.










The Hierarchical Clustering Algorithm



Steps








    

  • The dendrogram is obtained via an extremely simple algorithm:
    • 





    

  1. Initialize: Begin with \(n\) observations, treating each as its own cluster. Compute all \(\binom{n}{2} = n(n-1)/2\) pairwise dissimilarities (e.g., Euclidean distance).
    2. 

  2. Iterate (from \(i=n\) down to \(i=2\) clusters):
    

      

    1. Find Most Similar: Examine all pairwise inter-cluster dissimilarities among the \(i\) current clusters and identify the pair that are least dissimilar (most similar).
      2. 

    2. Fuse Clusters: Fuse these two clusters into a single new cluster. The dissimilarity between these two clusters indicates the height in the dendrogram at which the fusion should be placed.
      3. 

    3. Update Dissimilarities: Compute the new pairwise inter-cluster dissimilarities among the \(i-1\) remaining clusters (including the newly formed cluster).
      4. 

    3. 









Hierarchical Clustering



Dissimilarity Between Clusters (Linkage)








    

  • The algorithm requires defining how to measure the dissimilarity between two clusters if one or both contain multiple observations.
    • 






    

  • This is achieved by developing the notion of linkage, which defines the dissimilarity between two groups of observations.
    • 







Hierarchical Clustering



Linkage Types








    

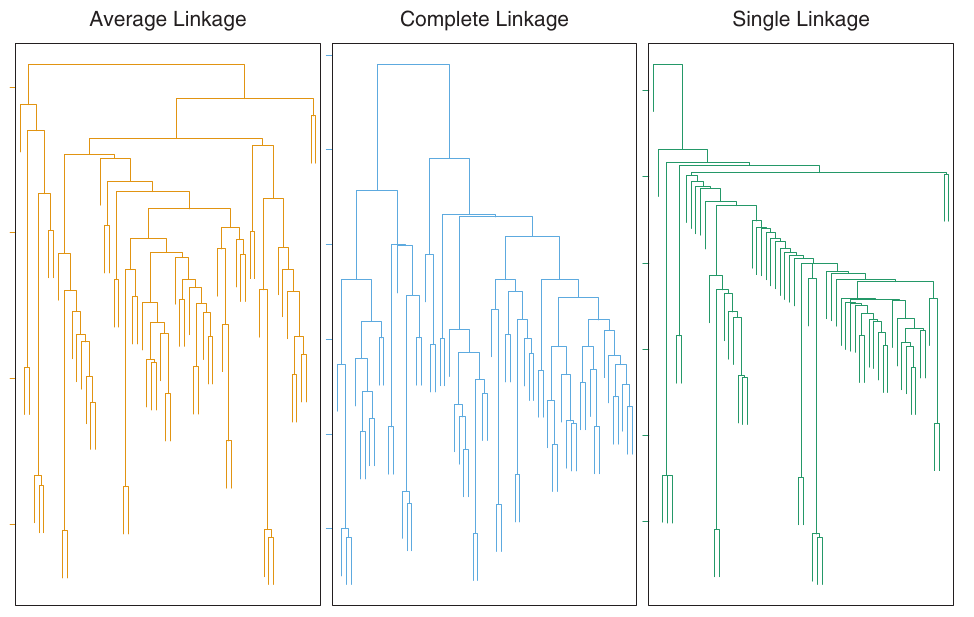
  • The four most common types of linkage are:
    • 







    

  • Complete Linkage: Maximal inter-cluster dissimilarity. Compute all pairwise dissimilarities between observations in cluster A and cluster B, and record the largest of these dissimilarities.
    • 

  • Single Linkage: Minimal inter-cluster dissimilarity. Compute all pairwise dissimilarities between observations in cluster A and cluster B, and record the smallest of these dissimilarities. Can result in extended, trailing clusters.
    • 





    

  • Average Linkage: Mean inter-cluster dissimilarity. Compute all pairwise dissimilarities between observations in cluster A and cluster B, and record the average of these dissimilarities.
    • 

  • Centroid Linkage: Dissimilarity between the centroid (mean vector) for cluster A and the centroid for cluster B. Can result in undesirable inversions.
    • 









Hierarchical Clustering



Linkage Type Impact





    

  • Average, complete, and single linkage are most popular.
    • 

  • Average and complete linkage are generally preferred as they tend to yield more balanced dendrograms.
    • 

  • Centroid linkage can suffer from an inversion, where two clusters are fused at a height below either of the individual clusters in the dendrogram. This can hinder visualization and interpretation.
    • 









Figure:


    

  • Shows how different linkage methods (Average, Complete, Single) applied to the same dataset produce different dendrogram structures.
    • 

  • Average and Complete linkage tend to yield more balanced clusters.
    • 





Three dendrograms for the same dataset, generated using Average, Complete, and Single linkage. Single linkage results in a very unbalanced tree, while Average and Complete are more balanced.










Choice of Dissimilarity Measure



Euclidean vs. Correlation-based








    

  • Euclidean distance is commonly used.
    • 

  • However, other dissimilarity measures might be preferred depending on the application.
    • 

  • Correlation-based distance considers two observations similar if their features are highly correlated, even if their observed values are far apart in terms of Euclidean distance.

      

    • This is an “unusual” use of correlation, normally computed between variables. Here, it’s computed between observation profiles.
      • 

    • Focuses on the shapes of observation profiles rather than their magnitudes.
      • 

    • 







Choice of Dissimilarity Measure



Example: Shopping Data








    

  • Consider an online retailer clustering shoppers based on purchase histories (items purchased).
    • 





    

  • If Euclidean distance is used, shoppers who bought very few items overall (infrequent users) might be clustered together, regardless of what they bought. This might not be desirable.
    • 





    

  • If correlation-based distance is used, shoppers with similar preferences (e.g., bought items A and B but never C or D) will be clustered together, even if some shoppers are high-volume and others low-volume. This might be a better choice for understanding preferences.
    • 







Choice of Dissimilarity Measure



Illustration












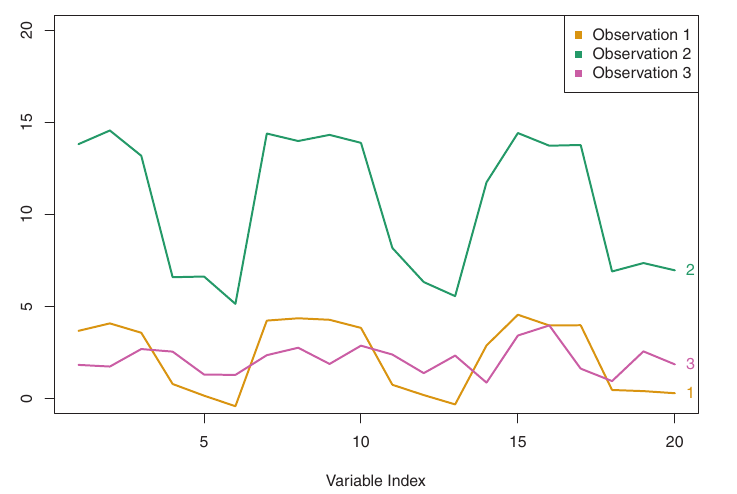
Figure:


    

  • Three observations with 20 variables.
    • 

  • Obs 1 & 3: Similar values, small Euclidean distance, weakly correlated, large correlation-based distance.
    • 

  • Obs 1 & 2: Different values, large Euclidean distance, highly correlated, small correlation-based distance.
    • 





Line plots of three observations across 20 variables. Illustrates cases where Euclidean distance differs from correlation-based distance based on value magnitude vs. profile shape.








Scaling Variables



Importance








    

  • Another crucial consideration: Should variables be scaled to have standard deviation one before computing dissimilarity?
    • 





    

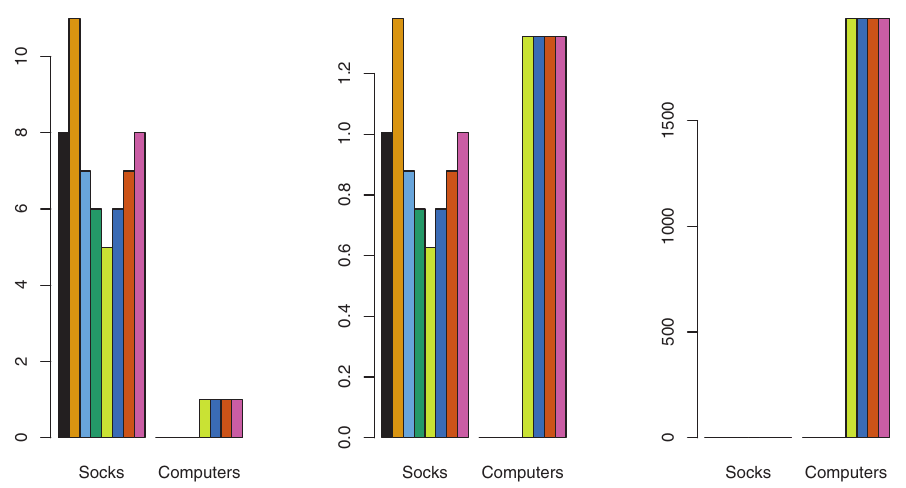
  • Example: Online Shopping (Socks vs. Computers)

      

    • A shopper buys 10 pairs of socks/year, but a computer rarely.
      • 

    • If raw values are used: Socks purchases (high frequency) will have a much larger effect on dissimilarities than computer purchases (low frequency).
      • 

    • This might be undesirable if the goal is to identify preference patterns for more valuable items like computers.
      • 

    • 







Scaling Variables



Illustration





    

  • If variables are scaled to have standard deviation one, each variable is given equal importance.
    • 

  • Also important when variables are measured on different scales (e.g., centimeters vs. kilometers). The choice of units can greatly affect the dissimilarity measure.
    • 









Figure:


    

  • Left: Raw purchases (socks dominate).
    • 

  • Center: Purchases scaled by standard deviation (computers now have greater relative effect).
    • 

  • Right: Dollars spent (computers clearly dominate due to price).
    • 

  • Clustering results will differ significantly based on these choices.
    • 





Bar plots showing purchase counts of socks and computers for 8 shoppers, under three different scaling scenarios: raw counts, counts scaled by standard deviation, and total dollars spent. Highlights the impact of scaling on variable importance.










R Example: Hierarchical Clustering



Synthetic Data for Demonstration








    

  • We will generate a small synthetic dataset to demonstrate hierarchical clustering, similar to the one in the Portuguese PDF.
    • 

  • This data will consist of 9 points in 2D space.
    • 







# A tibble: 9 × 3
     id    X1    X2
  <int> <dbl> <dbl>
1     1   0.1   0.4
2     2  -0.2  -0.3
3     3   0.5   0.9
4     4  -0.8  -0.7
5     5   0.7   0.1
6     6  -0.6  -0.5
7     7   0.8   0.3
8     8   0.6   0  
9     9  -0.1   1  










R Example: Hierarchical Clustering



Code - Hierarchical Clustering








    

  • We will use hclust for hierarchical clustering and cutree to obtain clusters.
    • 

  • dist() calculates the distance matrix.
    • 








# A tibble: 9 × 4
     id    X1    X2 cluster_h
  <int> <dbl> <dbl>     <int>
1     1   0.1   0.4         1
2     2  -0.2  -0.3         2
3     3   0.5   0.9         1
4     4  -0.8  -0.7         2
5     5   0.7   0.1         3
6     6  -0.6  -0.5         2
7     7   0.8   0.3         3
8     8   0.6   0           3
9     9  -0.1   1           1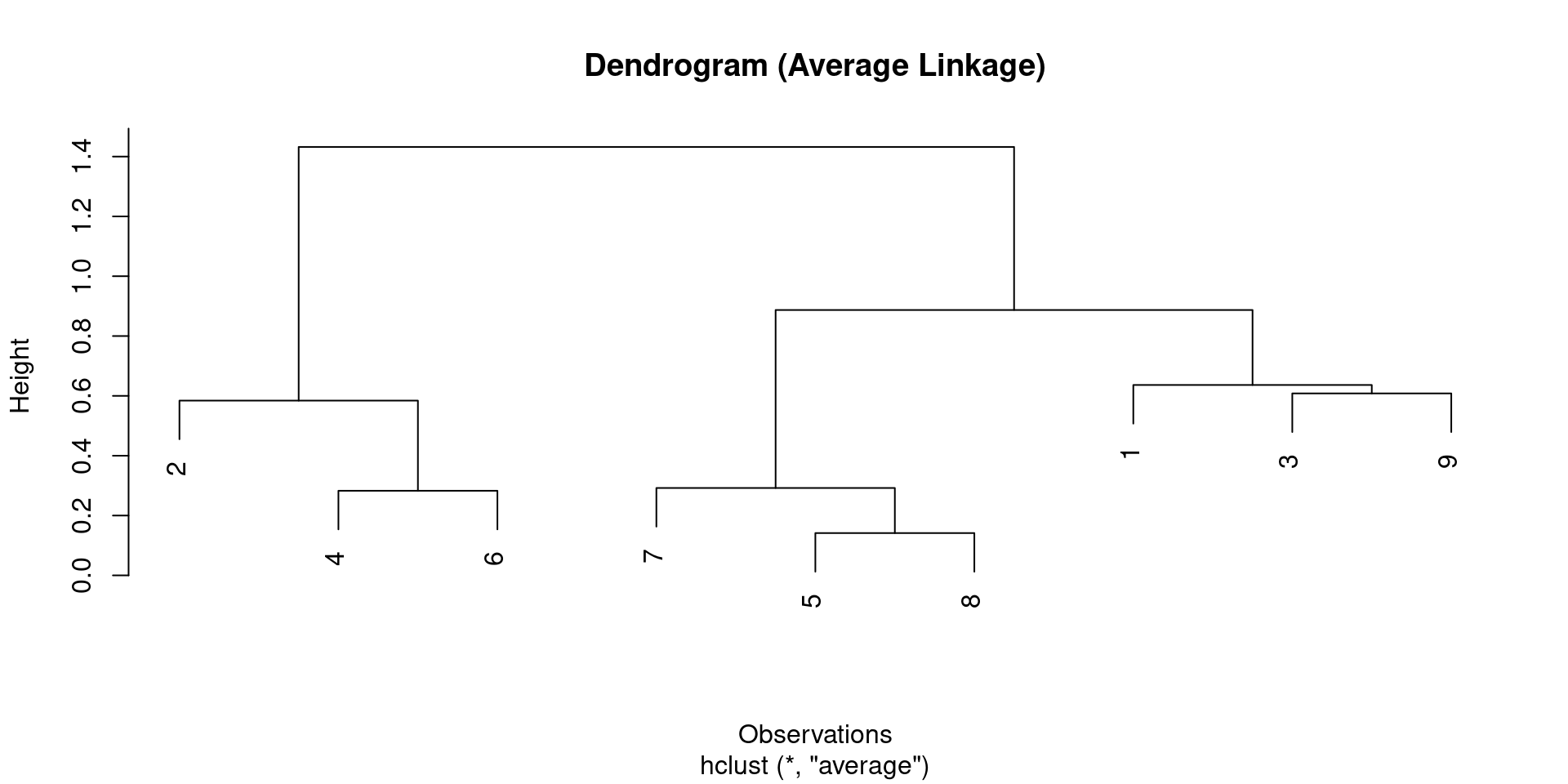










R Example: Hierarchical Clustering



Dendrogram Visualization








    

  • The plot generated by plot(dendrograma) is the standard R dendrogram.
    • 








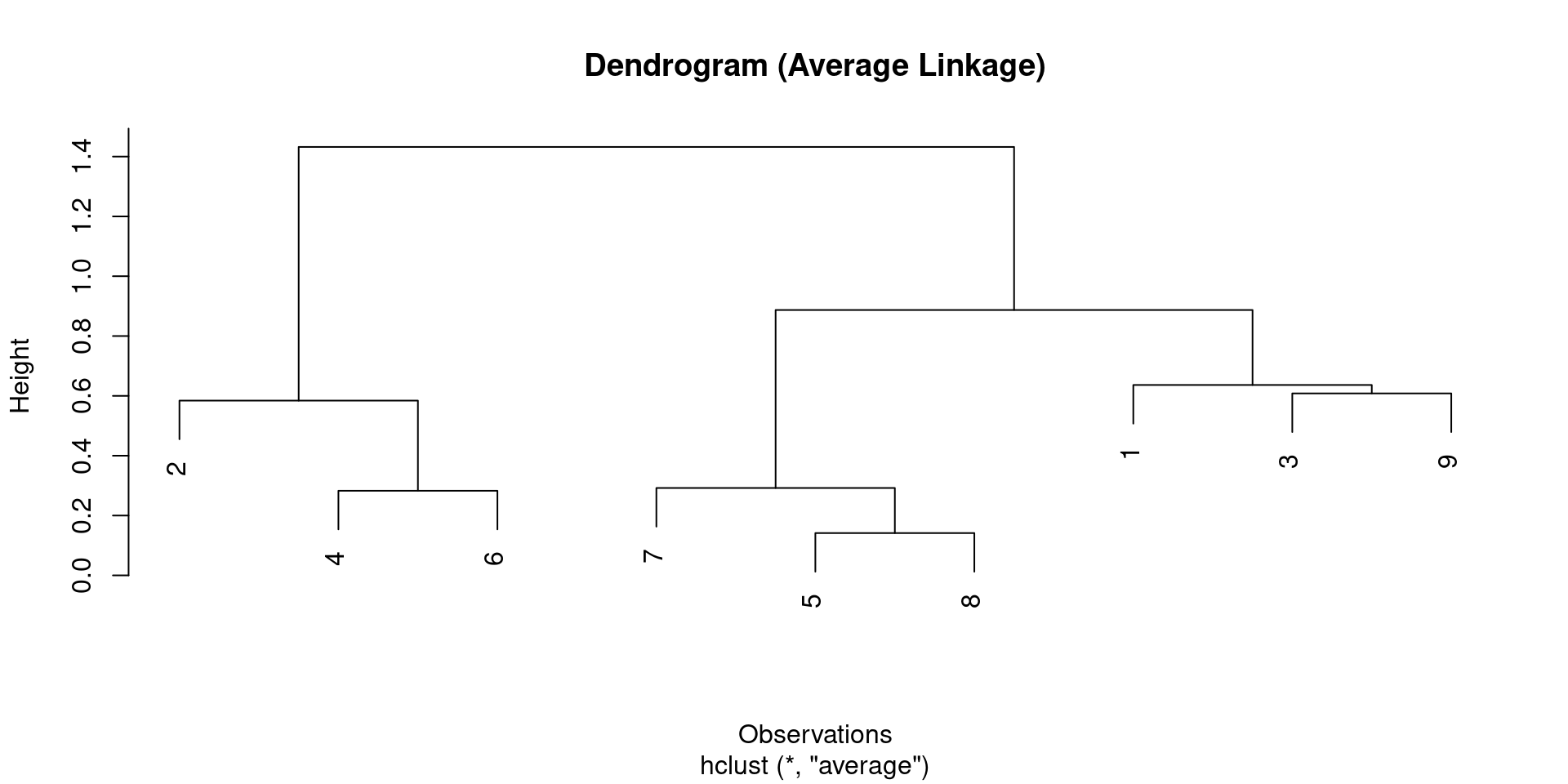
R Example: Hierarchical Clustering



Enhanced Visualization with factoextra








    

  • The factoextra package provides excellent tools for visualizing clustering results, including dendrograms with enhanced features.
    • 








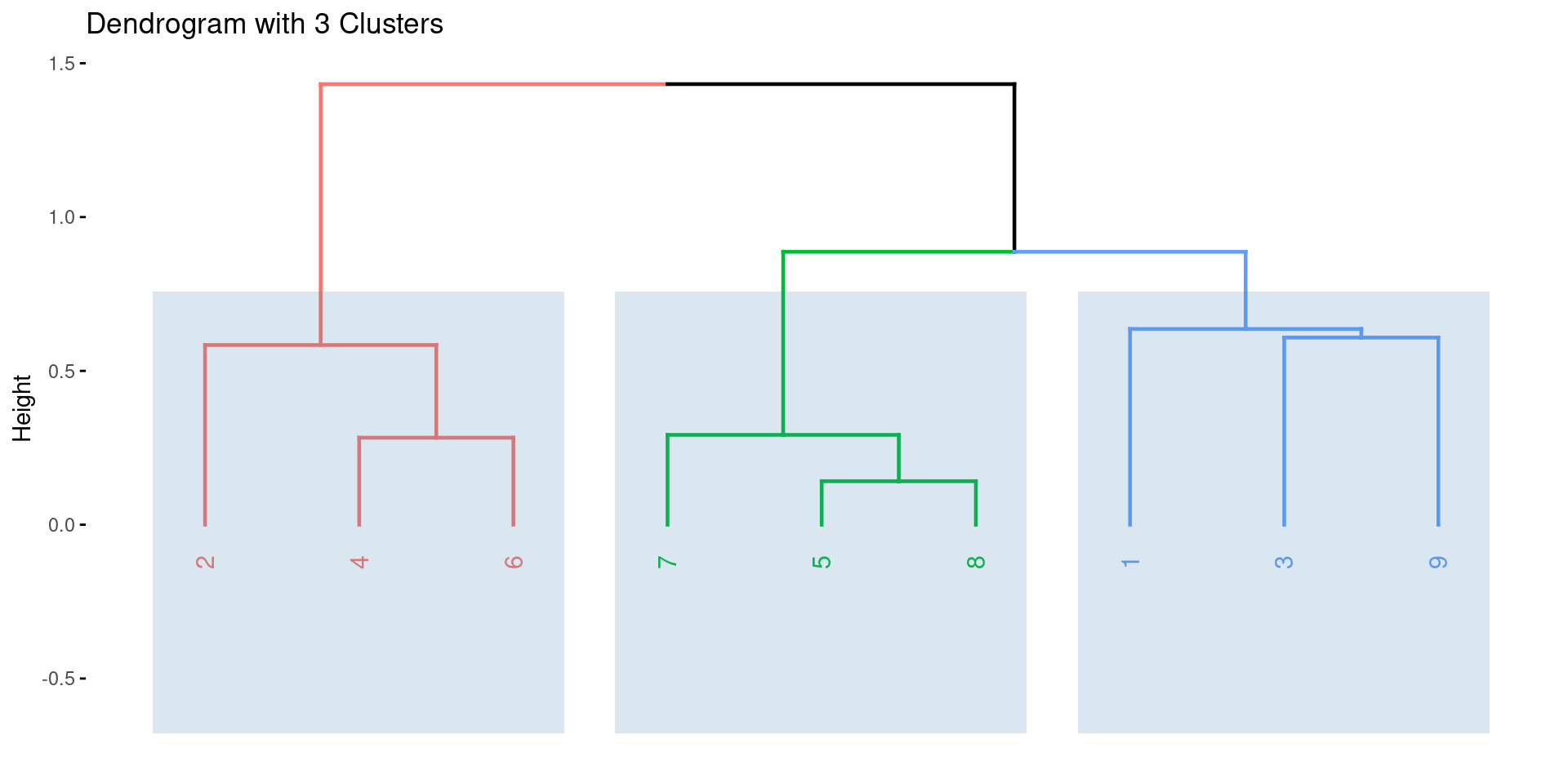
R Example: Hierarchical Clustering



Dendrogram with 3 Clusters













Practical Issues in Clustering



Small Decisions with Big Consequences








    

  • When performing clustering, several decisions must be made, which can strongly impact the results:
    • 





    

  • Data Standardization: Should observations or features be standardized (e.g., centered to mean zero, scaled to standard deviation one)?
    • 

  • Dissimilarity Measure (Hierarchical): What dissimilarity measure should be used (e.g., Euclidean, correlation-based)?
    • 

  • Linkage Type (Hierarchical): What type of linkage should be used (e.g., complete, average, single)?
    • 

  • Number of Clusters (K-Means & Hierarchical): How many clusters should be sought (\(K\) for K-Means, or where to cut the dendrogram)?
    • 










Practical Issues in Clustering



Validating the Clusters Obtained








    

  • Any clustering method will produce clusters. The critical question is: Do these clusters represent true subgroups in the data, or are they simply a result of clustering the noise?
    • 





    

  • Robustness: If we cluster the data again after removing a random subset of observations, would we obtain similar clusters? Often, this is not the case, indicating sensitivity to perturbations.
    • 





    

  • P-values: Techniques exist to assign a p-value to a cluster, assessing whether there is more evidence for the cluster than expected by chance. However, there is no consensus on a single best approach.
    • 







Practical Issues in Clustering



Other Considerations








    

  • Both K-Means and hierarchical clustering force every observation into a cluster.
    • 





    

  • This might be inappropriate if some observations are outliers that do not truly belong to any subgroup.
    • 





    

  • Mixture models are an attractive approach that can accommodate outliers and offer a “soft” version of K-Means clustering, where observations can belong to multiple clusters with certain probabilities.
    • 







Gaussian Mixture Models (GMM)



Probabilistic Soft Clustering







    

  • K-Means performs hard clustering, where each observation belongs to exactly one cluster.
    • 

  • Gaussian Mixture Models (GMM) assume that the data points are generated from a mixture of \(K\) different multivariate Gaussian distributions.
    • 

  • This allows for soft clustering, where each observation has a probability of belonging to each cluster (representing clustering uncertainty).
    • 



The Model:


    

  • The probability density function of the mixture model is: \[ p(\dot{\mathbf{x}}) = \sum_{k=1}^K \pi_k \mathcal{N}(\dot{\mathbf{x}} \mid \boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k) \] where
    • 









Gaussian Mixture Models (GMM)



Probabilistic Soft Clustering








\[ p(\dot{\mathbf{x}}) = \sum_{k=1}^K \pi_k \mathcal{N}(\dot{\mathbf{x}} \mid \boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k) \] where:


    

  • \(\pi_k\) is the mixture weight of the \(k\)-th component, satisfying \(0 \le \pi_k \le 1\) and \(\sum_{k=1}^K \pi_k = 1\).
    • 

  • \(\mathcal{N}(\dot{\mathbf{x}} \mid \boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k)\) is the multivariate Gaussian density with mean vector \(\boldsymbol{\mu}_k\) and covariance matrix \(\boldsymbol{\Sigma}_k\): \[ \mathcal{N}(\dot{\mathbf{x}} \mid \boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k) = \frac{1}{(2\pi)^{p/2} |\boldsymbol{\Sigma}_k|^{1/2}} \exp\left( -\frac{1}{2} (\dot{\mathbf{x}} - \boldsymbol{\mu}_k)^\top \boldsymbol{\Sigma}_k^{-1} (\dot{\mathbf{x}} - \boldsymbol{\mu}_k) \right) \]
    • 







Gaussian Mixture Models (GMM)



The EM Algorithm: E-Step








we still seek the maximum likelihood estimates of the parameters. However, the likelihood involves a logarithm of a sum over the mixture components, which complicates direct optimization.


    

  • To fit a GMM, we still seek the maximum likelihood estimates of the parameters. However, the likelihood involves a logarithm of a sum over the mixture components, which complicates direct optimization. \[ \ln p(\dot{\mathbf{X}} \mid \boldsymbol{\pi}, \boldsymbol{\mu}, \boldsymbol{\Sigma}) = \sum_{i=1}^n \ln \left( \sum_{k=1}^K \pi_k \mathcal{N}(\dot{\mathbf{x}}_i \mid \boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k) \right) \]
    • 

  • Instead, we use the Expectation-Maximization (EM) algorithm, which is an iterative optimization method.
    • 







Gaussian Mixture Models (GMM)



The EM Algorithm: E-Step








E-Step (Expectation):


    

  • Evaluate the posterior probabilities (also called responsibilities), which represent the probability that observation \(\dot{\mathbf{x}}_i\) belongs to component \(k\): \[ \gamma(z_{ik}) = P(z_{ik} = 1 \mid \dot{\mathbf{x}}_i) = \frac{\pi_k \mathcal{N}(\dot{\mathbf{x}}_i \mid \boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k)}{\sum_{j=1}^K \pi_j \mathcal{N}(\dot{\mathbf{x}}_i \mid \boldsymbol{\mu}_j, \boldsymbol{\Sigma}_j)} \] where \(z_{ik} \in \{0, 1\}\) is a latent variable indicating the component of origin.
    • 







Gaussian Mixture Models (GMM)



The EM Algorithm: M-Step








M-Step (Maximization):


    

  • Update the parameters using the responsibilities calculated in the E-step to maximize the expected complete-data log-likelihood:
    • 

  • Update Means: \[ \boldsymbol{\mu}_k^{\text{new}} = \frac{1}{N_k} \sum_{i=1}^n \gamma(z_{ik}) \dot{\mathbf{x}}_i, \quad \text{where } N_k = \sum_{i=1}^n \gamma(z_{ik}) \]
    • 







Gaussian Mixture Models (GMM)



The EM Algorithm: M-Step








    

  • Update Covariances: \[ \boldsymbol{\Sigma}_k^{\text{new}} = \frac{1}{N_k} \sum_{i=1}^n \gamma(z_{ik}) (\dot{\mathbf{x}}_i - \boldsymbol{\mu}_k^{\text{new}})(\dot{\mathbf{x}}_i - \boldsymbol{\mu}_k^{\text{new}})^\top \]
    • 

  • Update Mixture Weights: \[ \pi_k^{\text{new}} = \frac{N_k}{n} \]
    • 

  • Repeat E-step and M-step until the log-likelihood converges.
    • 







Gaussian Mixture Models (GMM)



Relationship with K-Means








    

  • GMM can be seen as a probabilistic generalization of K-Means.
    • 

  • If we assume that the covariance matrices are spherical and isotropic: \[ \boldsymbol{\Sigma}_k = \sigma^2 \mathbf{I} \] and we take the limit as the variance \(\sigma^2 \to 0\), then:

      

    • The responsibilities \(\gamma(z_{ik})\) become binary (0 or 1), assigning each point to its closest centroid.
      • 

    • The EM update for the means \(\boldsymbol{\mu}_k\) becomes exactly the K-Means centroid update.
      • 

    • 

  • Unlike K-Means, GMM allows for clusters of different volumes, shapes (via full covariance matrices \(\boldsymbol{\Sigma}_k\)), and orientations.
    • 








Evaluating Clustering Quality



Internal Metrics: Silhouette Coefficient








    

  • Since clustering is unsupervised, we often need internal metrics to evaluate the quality of the partition.
    • 

  • The Silhouette Coefficient measures how close each point is to points in its own cluster compared to points in other clusters.
    • 

  • For each observation \(i\):
    

      

    • \(a(i)\) = average distance from \(i\) to all other points in the same cluster.
      • 

    • \(b(i)\) = average distance from \(i\) to points in the nearest cluster of which \(i\) is not a member.
      • 

    • 







Evaluating Clustering Quality



Internal Metrics: Silhouette Coefficient





    

  • The silhouette width \(s(i)\) is defined as: \[ s(i) = \frac{b(i) - a(i)}{\max(a(i), b(i))} \]
    • 

  • \(s(i) \in [-1, 1]\):

      

    • \(s(i) \approx 1\): Well clustered (close to its cluster, far from others).
      • 

    • \(s(i) \approx 0\): Lies on the boundary between two clusters.
      • 

    • \(s(i) \approx -1\): Probably assigned to the wrong cluster.
      • 

    • 

  • The average silhouette width over all points is a measure of clustering quality.
    • 








Evaluating Clustering Quality



External Metrics: Adjusted Rand Index








    

  • When “true” class labels are known (e.g., in a benchmark simulation), we can evaluate a clustering by comparing it to the true labels.
    • 

  • The key idea: look at pairs of points and check whether the two partitions agree on whether each pair belongs to the same cluster or to different clusters.
    • 

  • The Rand Index (RI) measures the fraction of pairs on which the two partitions agree: \[ \text{RI} = \frac{a + b}{\binom{n}{2}} \]

      

    • \(a\) = number of pairs that are in the same cluster in both partitions.
      • 

    • \(b\) = number of pairs that are in different clusters in both partitions.
      • 

    • \(\binom{n}{2}\) = total number of pairs of points.
      • 

    • 







Evaluating Clustering Quality



Contingency Table





    

  • To compute \(a\) and \(b\) systematically, we organize the clusters of the two partitions into a contingency table:
    • 








\(V_1\)
\(V_2\)
\(\cdots\)
\(V_c\)
Sum






\(U_1\)
\(n_{11}\)
\(n_{12}\)
\(\cdots\)
\(n_{1c}\)
\(a_1\)




\(U_2\)
\(n_{21}\)
\(n_{22}\)
\(\cdots\)
\(n_{2c}\)
\(a_2\)




\(\vdots\)
\(\vdots\)
\(\vdots\)
\(\ddots\)
\(\vdots\)
\(\vdots\)




\(U_r\)
\(n_{r1}\)
\(n_{r2}\)
\(\cdots\)
\(n_{rc}\)
\(a_r\)




Sum
\(b_1\)
\(b_2\)
\(\cdots\)
\(b_c\)
\(n\)






    

  • \(U\) = true partition, \(V\) = estimated partition.
    • 

  • \(n_{ij}\) = number of points that belong to cluster \(U_i\) and cluster \(V_j\).
    • 

  • \(a_i = \sum_j n_{ij}\) (size of cluster \(U_i\)) and \(b_j = \sum_i n_{ij}\) (size of cluster \(V_j\)).
    • 







Evaluating Clustering Quality



Rewriting the Rand Index





    

  • Using the contingency table, the terms of the RI can be written as:
    • 



\[
a = \sum_{i,j} \binom{n_{ij}}{2}
\]


    

  • Pairs together in \(U\) (regardless of \(V\)): \(\sum_i \binom{a_i}{2}\)
    • 

  • Pairs together in \(V\) (regardless of \(U\)): \(\sum_j \binom{b_j}{2}\)
    • 





    

  • Therefore, \(b\) (pairs separated in both partitions) can be written as:
    • 



\[
b = \binom{n}{2} - \sum_i \binom{a_i}{2} - \sum_j \binom{b_j}{2} + \sum_{i,j} \binom{n_{ij}}{2}
\]






Evaluating Clustering Quality



The Problem of “Chance Agreement”








    

  • Problem: even two independent clusterings (with no real relationship) tend to have a high RI.
    • 

  • This happens because, with many small clusters, most pairs end up in different clusters in both partitions — contributing to \(b\) purely by chance.
    • 

  • We need a baseline: what would the RI be, on average, if \(U\) and \(V\) were random partitions with the same cluster sizes (\(a_i\) and \(b_j\) fixed)?
    • 

  • This baseline is the expected value of the Rand Index, \(\mathbb{E}[\text{RI}]\).
    • 







Evaluating Clustering Quality



Computing \(\mathbb{E}[\text{RI}]\)








    

  • We assume the generalized hypergeometric model : the row totals (\(a_i\)) and column totals (\(b_j\)) of the contingency table are fixed, while the values \(n_{ij}\) are distributed at random.
    • 




    

  • Under this model, it can be shown that:
    • 



\[
\mathbb{E}\left[\sum_{i,j} \binom{n_{ij}}{2}\right] = \frac{\left(\sum_i \binom{a_i}{2}\right)\left(\sum_j \binom{b_j}{2}\right)}{\binom{n}{2}}
\]


    

  • In other words: the expected amount of “pair agreement” depends only on the cluster sizes, not on any real correspondence between \(U\) and \(V\).
    • 

  • This value is the correction term that enters the ARI formula.
    • 







Evaluating Clustering Quality



External Metrics: Adjusted Rand Index





    

  • The Adjusted Rand Index (ARI) corrects the RI by subtracting this expectation and normalizing by the possible range:
    • 



\[ \text{ARI} = \frac{\text{RI} - \mathbb{E}[\text{RI}]}{\max(\text{RI}) - \mathbb{E}[\text{RI}]} \]


    

  • In terms of the contingency table, the explicit formula is:
    • 



\[
\text{ARI} = \frac{\displaystyle\sum_{i,j}\binom{n_{ij}}{2} - \dfrac{\sum_i\binom{a_i}{2}\sum_j\binom{b_j}{2}}{\binom{n}{2}}}
{\displaystyle\frac{1}{2}\left[\sum_i\binom{a_i}{2}+\sum_j\binom{b_j}{2}\right] - \dfrac{\sum_i\binom{a_i}{2}\sum_j\binom{b_j}{2}}{\binom{n}{2}}}
\]






Evaluating Clustering Quality



Interpreting the ARI








    

  • Numerator: the actual agreement gained above what is expected by chance.
    • 

  • Denominator: the maximum possible gain (when \(\text{RI} = 1\)).
    • 






    

  • \(\text{ARI} \in [-1, 1]\):

      

    • \(1.0\) → perfect agreement between the two partitions.
      • 

    • \(0.0\) → agreement equivalent to that expected by pure chance (independent clusterings).
      • 

    • \(< 0\) → agreement worse than chance (rare, but possible).
      • 

    • 





    

  • Unlike the RI, the ARI does not artificially increase with the number of clusters, which makes it the preferred metric for comparing clustering results in benchmarks.
    • 








Final Thoughts







    

  • Clustering is a powerful tool for discovering hidden structures in unlabeled data.
    • 






    

  • Choosing the right clustering method, dissimilarity measure, linkage type, and number of clusters is crucial and often application-specific.
    • 






    

  • Careful validation and consideration of practical issues like outliers and data perturbations are essential for meaningful results.
    • 








References







Basics


    

  • Aprendizado de Máquina: uma abordagem estatística, Izibicki, R. and Santos, T. M., 2020, link: https://rafaelizbicki.com/AME.pdf.
    • 

  • An Introduction to Statistical Learning: with Applications in R, James, G., Witten, D., Hastie, T. and Tibshirani, R., Springer, 2013, link: https://www.statlearning.com/.
    • 

  • Mathematics for Machine Learning, Deisenroth, M. P., Faisal. A. F., Ong, C. S., Cambridge University Press, 2020, link: https://mml-book.com.
    • 








References







Complementaries