Statistical Machine Learning

Classification Methods

Prof. Jodavid Ferreira

UFPE

Notation

  • \(X\) or \(Y\)
  • \(x\) or \(y\)
  • \(\mathbf{x}\) or \(\mathbf{y}\)
  • \(\dot{\mathbf{x}}\) or \(\dot{\mathbf{y}}\)
  • \(\mathbf{X}\) or \(\mathbf{Y}\)
  • \(\dot{\mathbf{X}}\) or \(\dot{\mathbf{Y}}\)


    

  • \(p\)
    • 

  • \(n\)
    • 

  • \(i\)
    • 

  • \(j\)
    • 

  • \(k\)
    • 





represent random variables (r.v.);


represent realizations of random variables;


represent random vectors;


represent realizations of random vectors;


represent random matrices;


represent realizations of random matrices;




dimension of features, variables, parameters


sample size


\(i\)-th observation, instance (e.g., \(i=1, ..., n\))


\(j\)-th feature, variable, parameter (e.g., \(j=1, ..., p\))


number of folds in k-fold CV








Remembering: Risk Function






    

  • Assume \(Y\) takes values in a set \(\mathcal{C}\) (e.g., \(\mathcal{C} = \{\text{spam, not spam}\}\)).
    • 





    

  • The regression risk function \(R(\hat{f}) = E[(Y - \hat{f}(\mathbf{x}))^2]\) is not suitable for classification (what would \(Y - \hat{f}(\mathbf{x})\) mean?).
    • 





    

  • A common risk function for classification is the 0-1 loss:
    • 





\[R(f) := E[I(Y \neq \hat{f}(\mathbf{x}))] = P(Y \neq \hat{f}(\mathbf{x}))\]




    

  • This is the probability of misclassification.
    • 

  • The loss function is
    • 



\[L(\hat{f}(\mathbf{x}), Y) = I(Y \neq \hat{f}(\mathbf{x}))\]






Optimal Classifier



Bayes Classifier







    

  • In regression, \(\hat{f}(\dot{\mathbf{x}}) = E[Y|\mathbf{x}=\dot{\mathbf{x}}]\) minimizes \(E[(Y - \hat{f}(\mathbf{x}))^2]\).
    • 





    

  • For classification, the function \(f\) that minimizes the 0-1 risk is given by: \[\hat{f}(\dot{\mathbf{x}}) = \underset{c \in \mathcal{C}}{\text{arg max }} P(Y=c|\mathbf{x}=\dot{\mathbf{x}})\]
    • 





    

  • This means \(\dot{\mathbf{x}}\) should be classified to the class with the highest posterior probability.
    • 





    

  • This is known as the Bayes classifier.
    • 





    

  • Like \(E[Y|\mathbf{x}=\dot{\mathbf{x}}]\) in regression, \(P(Y=c|\mathbf{x}=\dot{\mathbf{x}})\) is generally unknown.
    • 







Bayes Classifier







Theorem: Suppose we define the risk of a prediction function \(\hat{f}: \mathbb{R}^p \to \mathcal{C}\) via 0-1 loss: \(R(\hat{f}) = P(Y \neq \hat{f}(\mathbf{x}))\), where \((\mathbf{x},Y)\) is a new observation not used to estimate \(\hat{f}\).





Then the function \(\hat{f}\) that minimizes \(R(\hat{f})\) is given by





\[\hat{f}(x) = \underset{c \in \mathcal{C}}{\text{arg max }} P(Y=c|\mathbf{x}=\dot{\mathbf{x}})\]






Demonstration - Binary Case







    

  • Assume \(Y\) takes two values, \(c_1\) and \(c_2\) (binary problem).
    • 





\[\begin{align}
R(\hat{f}) = & E[I(Y \neq \hat{f}(\mathbf{x}))] = P(Y \neq \hat{f}(\mathbf{x})) \\
= & \int_{\mathbb{R}^p} P(Y \neq \hat{f}(\mathbf{x})|\mathbf{x}=\dot{\mathbf{x}})f(\mathbf{x})d\mathbf{x} \\
= & \int_{\mathbb{R}^p} [I(\hat{f}(\mathbf{x})=c_2)P(Y=c_1|\mathbf{x}=\dot{\mathbf{x}}) +\\
& I(\hat{f}(\dot{\mathbf{x}})=c_1)P(Y=c_2|\mathbf{x}=\dot{\mathbf{x}})]f(\mathbf{x})d\mathbf{x}
\end{align}\]


    

  • To minimize \(R(\hat{f})\), for each fixed \(\mathbf{x}\), we minimize the term in the square brackets.
    • 

  • This term is minimized if we choose \(\hat{f}(\dot{\mathbf{x}})=c_1\) when \(P(Y=c_1|\mathbf{x}=\dot{\mathbf{x}}) \ge P(Y=c_2|\mathbf{x}=\dot{\mathbf{x}})\), and \(\hat{f}(\dot{\mathbf{x}})=c_2\) otherwise.
    • 







Bayes Classifier for Binary Case







    

  • For the binary case, the Bayes classifier can be rewritten as:
    • 



\[ \hat{f}(\dot{\mathbf{x}}) = c_1 \iff P(Y=c_1|\mathbf{x}=\dot{\mathbf{x}}) \ge \frac{1}{2} \]





    

  • Observation: In binary classification, it’s common to denote classes in \(\mathcal{C}\) as 0 and 1. This is arbitrary and doesn’t imply an ordering.
    • 







Model Selection







    

  • To select a model \(\hat{f}\) from a class of models \(\mathcal{G}\): 
    

      

    1. Use cross-validation (or a validation set) to estimate \(R (\hat{f})\) for each \(\hat{f} \in \mathcal{F}\).
      2. 

    2. Choose the \(\hat{f}\) with the smallest estimated risk \(R (\hat{f})\).
      3. 

    • 






    

  • The following theorem shows this procedure likely returns the best model in \(\mathcal{G}\).
    • 







Model Selection Guarantee




Theorem: Let \(\mathcal{G} = \{\hat{f}_1, \dots, \hat{f}_T\}\) be a class of classifiers estimated from a training set. Let \(\tilde{R}(\hat{f})\) be the estimated error of \(\hat{f}\) on a validation set. Let \(\hat{f}^*\) be the model that minimizes the true risk \(R(\hat{f})\) among \(\hat{f} \in \mathcal{G}\), and let \(\hat{\tilde{f}}\) be the model that minimizes the estimated risk \(\tilde{R}(\hat{f})\) among \(\hat{f} \in \mathcal{G}\). Then, for any \(\epsilon > 0\), with probability at most \(\epsilon\): \[ |R(\hat{\tilde{f}}) - R(\hat{f}^*)| > 2 \sqrt{\frac{1}{2(n-s)} \log \frac{2T}{\epsilon}} \]




A more standard result (from the proof steps):


With probability at least \(1-\epsilon\), for all \(\hat{f} \in \mathcal{G}\),


\[R(\hat{\tilde{f}}) \le R(\hat{\tilde{f}}) + \delta \le R(\hat{f}^*) + \delta \le R(\hat{f}^*) + 2\delta,\]


where \(\delta = \sqrt{\frac{1}{2(n-s)}\log\frac{2T}{\epsilon}}\).






Implications of before Theorem







    

  • The larger the number of classifiers \(N\) in \(\mathcal{G}\), the lower the probability of recovering the best model (or the looser the bound).
    • 





    

  • This motivates comparing only a small set of final candidate models on the test set.
    • 





    

  • Tuning of each model (e.g., hyperparameter selection) should be done using cross-validation.
    • 





    

  • The final test set is reserved for comparing the best model from each class of models (e.g., best logistic regression vs. best KNN).
    • 








 
 
 
 





Plug-in Classifiers









Plug-in Classifiers







    

  • Theorem of Bayes classifier suggests a simple approach for prediction:

      

    1. Estimate \(P(Y=c|\mathbf{x}=\dot{\mathbf{x}})\) for each category \(c \in \mathcal{C}\).
      2. 

    2. Then, take \(\hat{f}(\mathbf{x}) = \underset{c \in \mathcal{C}}{\text{arg max }} \hat{P}(Y=c|\mathbf{x}=\dot{\mathbf{x}})\).
      3. 

    • 

  • For the binary case: \(\hat{f}(\dot{\mathbf{x}}) = 1 \iff \hat{P}(Y=1|\mathbf{x}=\dot{\mathbf{x}}) > 1/2\).
    • 





    

  • This approach is known as a plug-in classifier because we “plug in” an estimator of the conditional probability into the formula for the optimal \(\hat{f}\).
    • 





    

  • Creating a classifier boils down to estimating \(P(Y=c|\mathbf{x}=\dot{\mathbf{x}})\).
    • 







Regression Methods for Classification




    

  • Note that for any \(c \in \mathcal{C}\), \(P(Y=c|\mathbf{x}=\dot{\mathbf{x}}) = E[I(Y=c)|\mathbf{x}=\dot{\mathbf{x}}]\).
    • 

  • Let \(Z_c = I(Y=c)\). We can use any regression model (trees, forests, etc.) to estimate \(E[Z_c|\mathbf{x}=\dot{\mathbf{x}}]\).
    • 

  • Example: Linear regression to estimate \(P(Y=c|\mathbf{x}=\dot{\mathbf{x}})\): \[ P(Y=c|\mathbf{x}=\dot{\mathbf{x}}) = E[Z_c|\mathbf{x}=\dot{\mathbf{x}}] \approx \beta_0^{(c)} + \beta_1^{(c)}x_1 + \dots + \beta_p^{(c)}x_p \]
    • 

  • Coefficients can be estimated using OLS, Lasso, etc.
    • 

  • Estimates \(\hat{P}(Y=c|\mathbf{x}=\dot{\mathbf{x}})\) might be \(<0\) or \(>1\), but can still be used in the plug-in classifier.
    • 

  • This is problematic, but methods like logistic regression constrain probabilities to \([0,1]\).
    • 








Logistic Regression







    

  • Assume \(Y\) is binary, \(\mathcal{C}=\{0,1\}\).
    • 





    

  • Logistic regression models \(P(Y=1|\mathbf{x}=\dot{\mathbf{x}})\) with a parametric form: \[ P(Y=1|\mathbf{x}=\dot{\mathbf{x}}) = \frac{e^{\eta(\dot{\mathbf{x}})}}{1 + e^{\eta(\dot{\mathbf{x}})}} = \frac{1}{1 + e^{-\eta(\dot{\mathbf{x}})}} \] where \(\eta(\dot{\mathbf{x}}) = \beta_0 + \beta_1x_1 + \dots + \beta_px_p\).
    • 





    

  • This is the sigmoid (or logistic) function applied to a linear combination of \(x\).
    • 





    

  • We don’t assume this relationship is perfectly true, but hope it leads to a good classifier.
    • 







Logistic Regression



Estimating Coefficients








    

  • Coefficients \(\beta\) are estimated using Maximum Likelihood Estimation (MLE).
    • 





    

  • Given i.i.d. data \((\mathbf{x}_k, Y_k)\), the conditional likelihood is: \[ L(\mathbf{y}; (\dot{\mathbf{X}}, \beta)) = \prod_{k=1}^n [P(Y_k=1|\dot{\mathbf{x}}_k, \beta)]^{Y_k} [1 - P(Y_k=1|\dot{\mathbf{x}}_k, \beta)]^{1-Y_k} \]
    • 





    

  • Maximize \(L\) (or typically \(\log L\)) to find \(\hat{\beta}\).

      

    • Numerical optimization algorithms are required.
      • 

    • 









Naive Bayes







    

  • Another approach to estimate \(P(Y=c|\mathbf{x}=\dot{\mathbf{x}})\) uses Bayes’ Theorem directly.
    • 





    

  • Assuming \(\mathbf{x}\) is a vector of continuous covariates: \[ P(Y=c|\mathbf{x}=\dot{\mathbf{x}}) = \frac{f(\dot{\mathbf{x}}|Y=c)P(Y=c)}{\sum_{s \in \mathcal{C}} f(\dot{\mathbf{x}}|Y=s)P(Y=s)} \]
    • 





    

  • We need to estimate:

      

    • Marginal probabilities \(P(Y=s)\)

        

      • prior probabilities of classes, e.g., from sample proportions
        • 

      • 

    • Conditional densities \(f(\dot{\mathbf{x}}|Y=s)\)

        

      • class-conditional densities of features
        • 

      • 

    • 







The “Naive” Assumption







    

  • Estimating \(f(\dot{\mathbf{x}}|Y=s)\) for multivariate \(\dot{\mathbf{x}}\) can be hard (curse of dimensionality).
    • 





    

  • The Naive Bayes method assumes conditional independence of features given the class: \[ f(\dot{\mathbf{x}}|Y=s) = f((x_1, \dots, x_p)|Y=s) = \prod_{j=1}^p f(x_j|Y=s) \]
    • 

  • This assumption is often unrealistic (“naive”) but makes estimation tractable and can lead to surprisingly good classifiers.
    • 





    

  • Now, we only need to estimate univariate densities \(f(x_j|Y=s)\).

      

    • E.g., assume \(X_j|Y=s \sim N(\mu_{j,s}, \sigma^2_{j,s})\). Parameters estimated via MLE.
      • 

    • 







Naive Bayes



Implementation Details





    

  • If \(X_j|Y=s \sim N(\mu_{j,s}, \sigma^2_{j,s})\):

      

    • \(\hat{\mu}_{j,s} = \frac{1}{|C_s|} \sum_{k \in C_s} X_{jk}\)
      • 

    • \(\hat{\sigma}^2_{j,s} = \frac{1}{|C_s|} \sum_{k \in C_s} (X_{jk} - \hat{\mu}_{j,s})^2\), where \(C_s = \{k : Y_k = s\}\)
      • 

    • 

  • Other distributions can be used. For discrete features \(X_j\), we estimate \(P(X_j=x_j|Y=s)\) (e.g., from counts).
    • 

  • Observation (Numerical Stability): Products \(\prod f(x_k|Y=c)\) can be numerically unstable (underflow if terms are small). It’s better to work with log-probabilities: \[ \log P(Y=c|\mathbf{x}=\dot{\mathbf{x}}) \propto \sum_{j=1}^p \log f(x_j|Y=c) + \log P(Y=c) \] Classify to \(c\) that maximizes this sum.
    • 







Naive Bayes













Discriminant Analysis










    

  • Naive Bayes assumes \(f(\dot{\mathbf{x}}|Y=c) = \prod\limits_{j=1}^{p} f(x_j|Y=c)\).
    • 






    

  • Discriminant Analysis makes other assumptions, typically that \(\mathbf{X}|Y=c\) follows a multivariate normal distribution.
    • 







Linear Discriminant Analysis (LDA)







    

  • LDA assumes that \(\mathbf{X}|Y=c \sim N(\mathbf{\mu}_c, \Sigma)\).
    

      

    • Each class \(c\) has its own mean vector \(\mathbf{\mu}_c\).
      • 

    • All classes share a common covariance matrix \(\Sigma\).
      • 

    • 

  • The density is:
    

    \[f(\dot{\mathbf{x}}|Y=c) = \frac{1}{(2\pi)^{p/2}|\Sigma|^{1/2}} \exp\left(-\frac{1}{2}(\dot{\mathbf{x}}-\mathbf{\mu}_c)^\top\Sigma^{-1}(\dot{\mathbf{x}}-\mathbf{\mu}_c)\right)\]
    • 

  • Parameters \(\mathbf{\mu}_c, \Sigma\) are estimated from data (MLE).
    

      

    • \(\hat{\mathbf{\mu}}_c =\) sample mean of \(\dot{\mathbf{x}}\) for class \(c\).
      • 

    • \(\hat{\Sigma} =\) pooled sample covariance matrix.
      • 

    • 







LDA Decision Boundary




    

  • The plug-in classifier is \(\hat{f}(\dot{\mathbf{x}}) = \underset{c \in \mathcal{C}}{\text{arg max }} \hat{f}(\dot{\mathbf{x}}|Y=c)\hat{P}(Y=c)\).
    • 





    

  • For binary classification (\(Y \in \{0,1\}\)), the decision rule
    • 



\[P(Y=1|\dot{\mathbf{x}})/P(Y=0|\dot{\mathbf{x}}) > K \, (\text{or }\log P(Y=1|\dot{\mathbf{x}}) - \log P(Y=0|\dot{\mathbf{x}}) > K')\]


simplifies to a linear function of \(x\): \[ \delta_1(\dot{\mathbf{x}}) - \delta_0(\dot{\mathbf{x}}) > K''\] 


where \(\delta_c(\dot{\mathbf{x}}) = \dot{\mathbf{x}}^\top\Sigma^{-1}\mu_c - \frac{1}{2}\mu_c^\top\Sigma^{-1}\mu_c + \log P(Y=c)\).


    

  • The decision boundary is a hyperplane in \(\mathbb{R}^p\).
    • 








Quadratic Discriminant Analysis







    

  • QDA also assumes \(\mathbf{X}|Y=c\) is multivariate normal, but allows each class to have its own covariance matrix \(\Sigma_c\): \[\mathbf{X}|Y=c \sim N(\mu_c, \Sigma_c) \]
    • 






    

  • The density \(f(\dot{\mathbf{x}}|Y=c)\) uses \(\mu_c\) and \(\Sigma_c\).
    • 






    

  • Parameters \(\mu_c, \Sigma_c\) are estimated via MLE for each class.

      

    • \(\hat{\Sigma}_c =\) sample covariance matrix for class \(c\).
      • 

    • 







QDA Decision Boundary




    

  • The plug-in classifier is
    • 



\[\hat{f}(\dot{\mathbf{x}}) = \underset{c \in \mathcal{C}}{\text{arg max }} \hat{f}(\dot{\mathbf{x}}|Y=c)\hat{P}(Y=c)\]




    

  • For binary classification, the decision rule involves terms quadratic in \(\dot{\mathbf{x}}\) (due to \(\dot{\mathbf{x}}^\top\Sigma_c^{-1}\dot{\mathbf{x}}\)). \[ \delta_1(\dot{\mathbf{x}}) - \delta_0(\dot{\mathbf{x}}) > K'' \] where \(\delta_c(\dot{\mathbf{x}}) = -\frac{1}{2}\log|\Sigma_c| - \frac{1}{2}(\dot{\mathbf{x}}-\mu_c)^\top\Sigma_c^{-1}(\dot{\mathbf{x}}-\mu_c) + \log P(Y=c)\).
    • 





    

  • The decision boundary is a quadratic surface in \(\mathbb{R}^p\).
    • 








Example: LDA vs QDA














Predicted values by (a) LDA and (b) QDA. QDA provides better classifications in this simulated example.

















Test set with true labels.








    

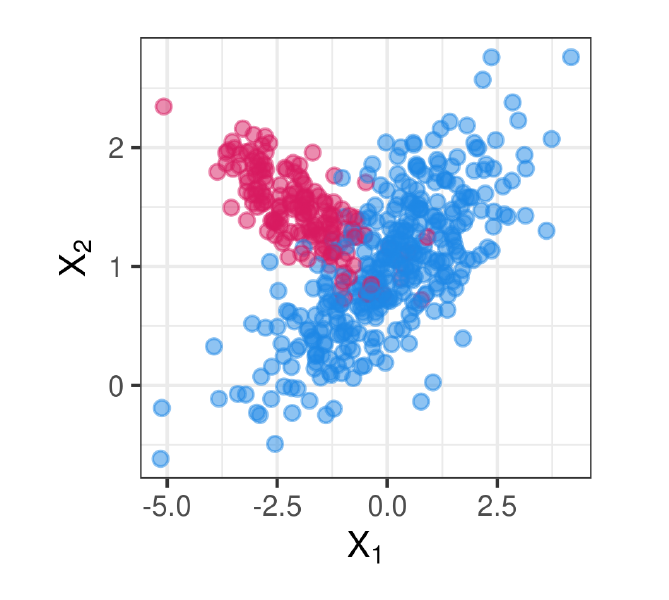
  • QDA is more flexible than LDA but requires estimating more parameters (can overfit if \(p\) is large and \(n\) is small). LDA is less flexible but more stable.
    • 







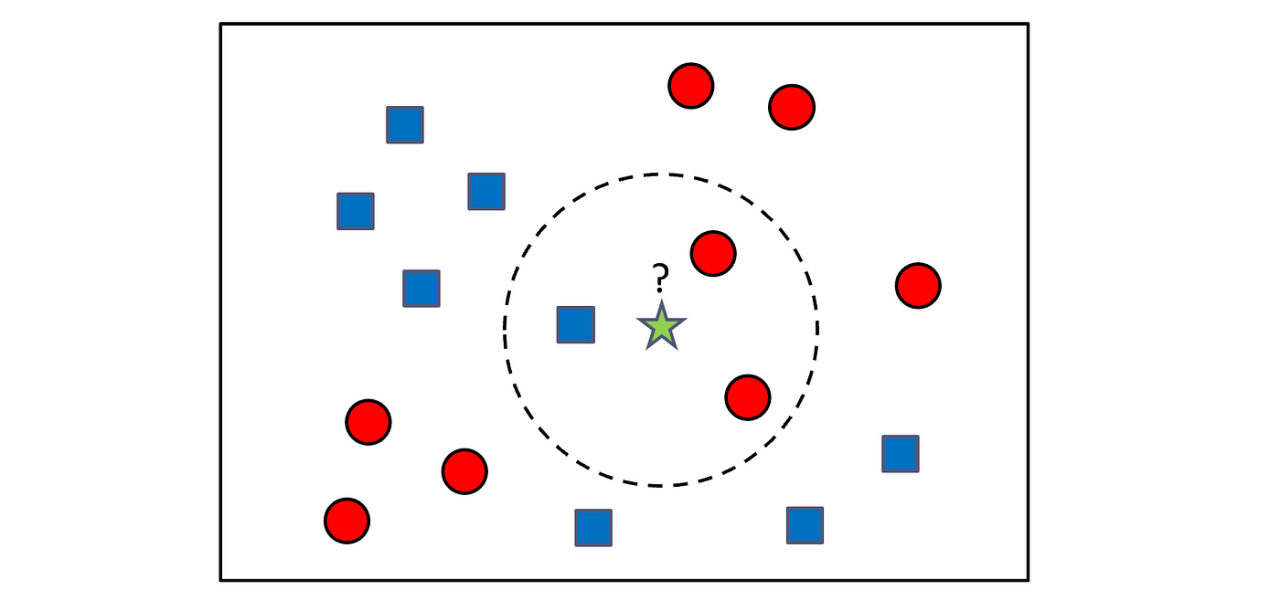
k-Nearest Neighbors (k-NN)







    

  • k-NN adapts trivially to classification.
    • 





    

  • Classifier \(\hat{f}(\dot{\mathbf{x}}) = \text{mode}\{y_i : \dot{\mathbf{x}}_i \in N_x\}\), where \(N_\dot{\mathbf{x}}\) is the set of \(k\) training samples nearest to \(\dot{\mathbf{x}}\).
    • 





    

  • Prediction is the majority class among the \(k\) neighbors.
    • 








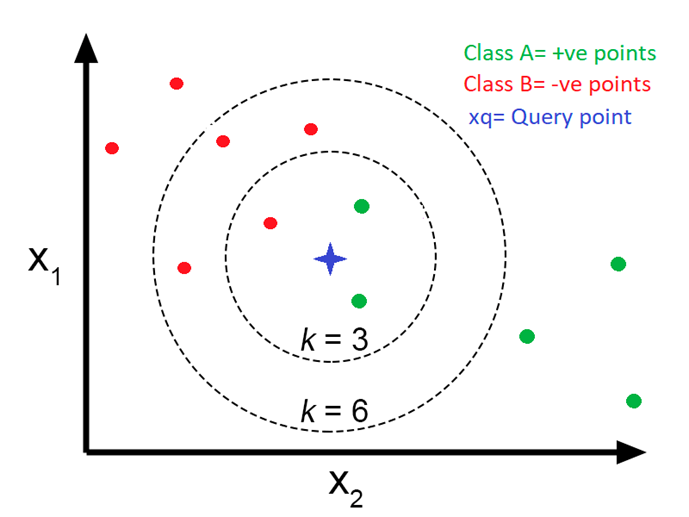
k-NN Classifier







Thus, the predicted class of observation \(\mathbf{x}_0\) is defined by the k-NN Classifier as:


\[\hat{y} = \underset{i \in \mathcal{N}_{\mathbf{x_0}}}{\text{mode }} y_{i},\]


where \(\mathcal{N}_{\mathbf{x_0}}\) is the set of the \(k\) nearest observations to \(\mathbf{x}_0\). We can also write it in terms of probability:


\[\hat{y}  = \underset{y}{\text{arg max }} P(f(\mathbf{x_0}) = y)=\frac{1}{k} \sum_{i \in k} I(y_i = y),\]









And how do we find the k nearest observations to \(\mathbf{x_0}\)?









k-NN Classifier







    

  • The k-NN Classifier selects the \(k\) nearest neighbors by calculating distances between the values of the training observations and the test observation.
    • 





    

  • A distance is a function that measures the dissimilarity between two observations and has some properties.
    • 







    

  • Consider any two vectors \(\mathbf{x}_i\) and \(\mathbf{x}_j\); the distance \(d(\mathbf{x}_i, \mathbf{x}_j)\) must satisfy the following properties:
    

      

    • \(d(\mathbf{x}_i, \mathbf{x}_j) \geq 0\) for all \(i\) and \(j\);
      • 

    • \(d(\mathbf{x}_i, \mathbf{x}_j) = 0\) if, and only if, \(\mathbf{x}_i = \mathbf{x}_j\);
      • 

    • \(d(\mathbf{x}_i, \mathbf{x}_j) = d(\mathbf{x}_j, \mathbf{x}_i)\) (Symmetry);
      • 

    • \(d(\mathbf{x}_i, \mathbf{x}_j) \leq d(\mathbf{x}_i, \mathbf{x}_k) + d(\mathbf{x}_k, \mathbf{x}_j)\), given a third vector \(\mathbf{x}_k\) (Triangle inequality).
      • 

    • 









k-NN Classifier







    

  • The most common distances are the Euclidean distance and the Mahalanobis distance.
    • 












The Euclidean distance between two vectors \(\mathbf{x}_i\) and \(\mathbf{x}_j\) is given by:




\[d(\mathbf{x}_i, \mathbf{x}_j) = \sqrt{\sum_{l=1}^{p} (x_{il} - x_{jl})^2}.\]










k-NN Classifier











The Mahalanobis distance is given by:




\[d(\mathbf{x}_i, \mathbf{x}_j) = \sqrt{(\mathbf{x}_i - \mathbf{x}_j)^\top \mathbf{\Sigma}^{-1} (\mathbf{x}_i - \mathbf{x}_j)},\] where \(\mathbf{\Sigma}\) is the covariance matrix of the training data.








k-NN Classifier








Some important points:






    

  • Since the \(k\)-NN algorithm uses distances, this implies an assumption that all variables (features) must be numerical.
    • 






    

  • Another important point is that the Euclidean distance is sensitive to the scale of the variables, so it is advisable to standardize the variables.
    • 






    

  • The Mahalanobis distance is an alternative for correlated variables.
    • 







k-NN Classifier













k-NN Classifier













Others Methods







    

  • Decision Tree;
    • 






    

  • Random Forest;
    • 






    

  • Support Vector Machine;
    • 









References







Basics


    

  • Aprendizado de Máquina: uma abordagem estatística, Izibicki, R. and Santos, T. M., 2020, link: https://rafaelizbicki.com/AME.pdf.
    • 

  • An Introduction to Statistical Learning: with Applications in R, James, G., Witten, D., Hastie, T. and Tibshirani, R., Springer, 2013, link: https://www.statlearning.com/.
    • 

  • Mathematics for Machine Learning, Deisenroth, M. P., Faisal. A. F., Ong, C. S., Cambridge University Press, 2020, link: https://mml-book.com.
    • 








References







Complementaries