Statistical Machine Learning

SVM

Prof. Jodavid Ferreira

UFPE

Notation

  • \(X\) or \(Y\)
  • \(x\) or \(y\)
  • \(\mathbf{x}\) or \(\mathbf{y}\)
  • \(\dot{\mathbf{x}}\) or \(\dot{\mathbf{y}}\)
  • \(\mathbf{X}\) or \(\mathbf{Y}\)
  • \(\dot{\mathbf{X}}\) or \(\dot{\mathbf{Y}}\)


    

  • \(p\)
    • 

  • \(n\)
    • 

  • \(i\)
    • 

  • \(j\)
    • 

  • \(k\)
    • 





represent random variables (r.v.);


represent realizations of random variables;


represent random vectors;


represent realizations of random vectors;


represent random matrices;


represent realizations of random matrices;




dimension of features, variables, parameters


sample size


\(i\)-th observation, instance (e.g., \(i=1, ..., n\))


\(j\)-th feature, variable, parameter (e.g., \(j=1, ..., p\))


number of folds in k-fold CV








Support Vector Machines










    

  • This class discusses the Support Vector Machine (SVM), an approach for classification.
    • 





    

  • Developed in the computer science community in the 1990s.
    • 





    

  • Known for good performance in various settings.
    • 







Overview of Topics




    

  1. Maximal Margin Classifier (MMC)

      

    • Intuitive, simple, but limited (requires linearly separable classes).
      • 

    2. 

  2. Support Vector Classifier (SVC)

      

    • Extension of MMC for broader cases (handles non-separable data with a “soft margin”).
      • 

    3. 

  3. Support Vector Machine (SVM)

      

    • Further extension of SVC for non-linear class boundaries using kernels.
      • 

    4. 

  4. Multi-class SVMs

      

    • Extending SVMs for more than two classes.
      • 

    5. 

  5. Relationship to Logistic Regression
    6. 



People often loosely refer to all three (MMC, SVC, SVM) as “support vector machines”. We will distinguish them.








 
 
 
 
 





Maximal Margin Classifier (MMC)









Maximal Margin Classifier



What Is a Hyperplane?





    

  • In a \(p\)-dimensional space, a hyperplane is a flat affine subspace of dimension \(p-1\).

      

    • In 2D: a line.
      • 

    • In 3D: a plane.
      • 

    • 

















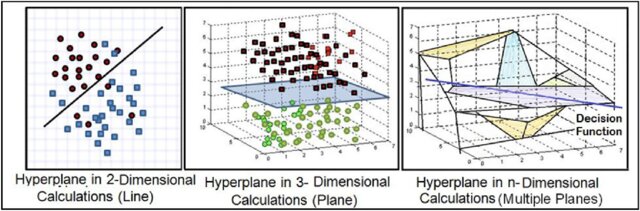
Maximal Margin Classifier



What Is a Hyperplane?








    

  • Mathematically, defined by: \[ \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \dots + \beta_p X_p = 0 \]
    • 






    

  • A point \(\mathbf{x} = (X_1, \dots, X_p)^T\) lies on the hyperplane if it satisfies the equation.
    • 






    

  • An affine subspace need not pass through the origin.
    • 







Hyperplanes for Classification




    

  • If a point \(\mathbf{x}\) does not satisfy \(\beta_0 + \sum_{j=1}^p \beta_j X_j = 0\):

      

    • If \(\beta_0 + \sum_{j=1}^p \beta_j X_j > 0\), \(X\) lies on one side of the hyperplane.
      • 

    • If \(\beta_0 + \sum_{j=1}^p \beta_j X_j < 0\), \(X\) lies on the other side.
      • 

    • 

  • A hyperplane divides \(p\)-dimensional space into two halves.
    • 

  • We can determine which side a point lies on by the sign of \(f(\mathbf{x}) = \beta_0 + \sum_{j=1}^p \beta_j X_j\).
    • 


















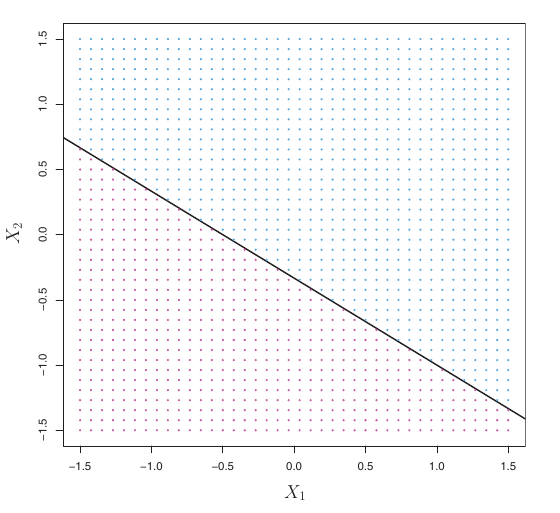
Classification



Using a Separating Hyperplane





    

  • Suppose we have \(n\) training observations \(x_1, \dots, x_n\) in \(p\)-dimensional space, with class labels \(y_1, \dots, y_n \in \{-1, 1\}\).
    • 

  • A separating hyperplane perfectly separates training observations by class:
    

      

    • \(\beta_0 + \beta_1 x_{i1} + \dots + \beta_p x_{ip} > 0\) if \(y_i = 1\)
      • 

    • \(\beta_0 + \beta_1 x_{i1} + \dots + \beta_p x_{ip} < 0\) if \(y_i = -1\)
      • 

    • 

  • This can be written concisely as: \[ y_i (\beta_0 + \beta_1 x_{i1} + \dots + \beta_p x_{ip}) > 0 \quad \text{for all } i=1, \dots, n \]
    • 

  • If a separating hyperplane exists, we can use it for classification. A new observation \(\mathbf{x}^*\) is classified based on the sign of \(f(\mathbf{x}^*) = \beta_0 + \sum \beta_j x_j^*\).
    • 







Infinite Separating Hyperplanes











    

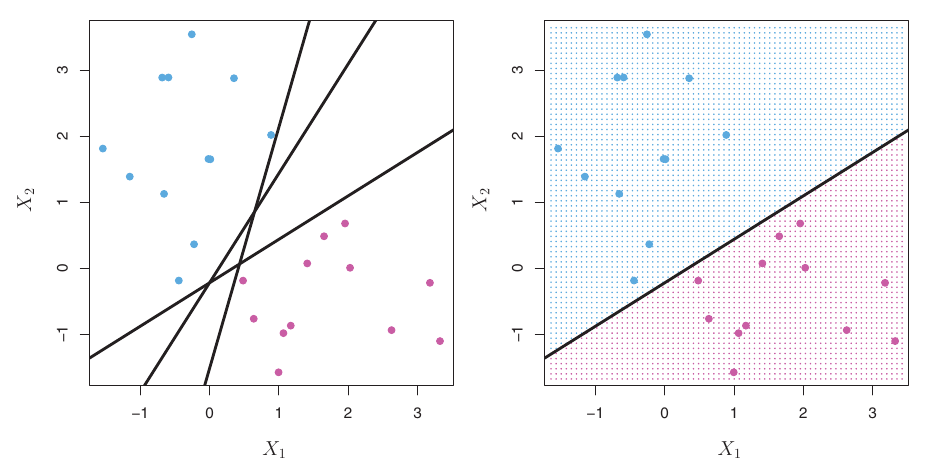
  • If data is linearly separable, there are usually an infinite number of separating hyperplanes.
    • 

  • A given separating hyperplane can often be shifted or rotated slightly without misclassifying any training points.
    • 

  • Which one to choose? We need a systematic way to pick the “best” one.
    • 







The Maximal Margin Classifier (MMC)







    

  • The maximal margin hyperplane (or optimal separating hyperplane) is the separating hyperplane that is farthest from the training observations.
    • 





    

  • Margin: The minimal perpendicular distance from any training observation to the hyperplane.
    • 





    

  • The MMC maximizes this margin.
    • 





    

  • The intuition is that a larger margin leads to better generalization on test data.
    • 





    

  • Observations that lie on the margin (equidistant from the hyperplane) are called support vectors.
    • 







The Maximal Margin Classifier (MMC)















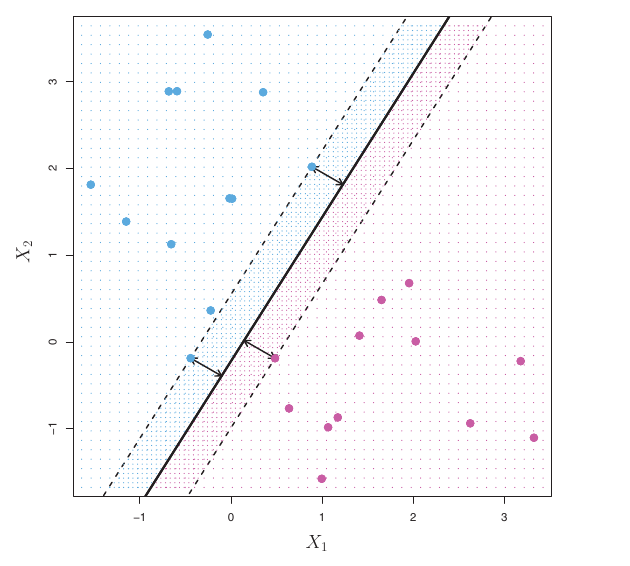
Support Vectors







    

  • Support Vectors are the training observations that are exactly on the margin.
    • 





    

  • These vectors “support” the hyperplane. If a support vector is moved, the maximal margin hyperplane would also move.
    • 





    

  • The MMC depends only on these support vectors. Other observations can be moved (as long as they don’t cross the margin) without affecting the hyperplane.
    • 





    

  • This property is crucial and will reappear with SVC and SVM.
    • 







Construction of the MMC




The MMC is the solution to the optimization problem:


Maximize \(M\) (the margin) with respect to \(\beta_0, \beta_1, \dots, \beta_p, M\) Subject to:


    

  1. \(\sum_{j=1}^p \beta_j^2 = 1\)
    2. 

  2. \(y_i (\beta_0 + \beta_1 x_{i1} + \dots + \beta_p x_{ip}) \ge M \quad \forall i=1, \dots, n\)
    3. 

  3. \(M > 0\)
    4. 



    

  • Constraint (1) normalizes the \(\beta_j\)’s. Without it, we could increase \(M\) by scaling \(\beta_0, \dots, \beta_p\).
    • 

  • Constraint (2) ensures each observation is on the correct side of the hyperplane and at least distance \(M\) away.
    • 

  • With \(\sum \beta_j^2 = 1\), the perpendicular distance from observation \(x_i\) to the hyperplane is \(y_i (\beta_0 + \sum \beta_j x_{ij})\).
    • 







The Non-Separable Case




    

  • The MMC is great if a separating hyperplane exists.
    • 





    

  • However, in many real-world datasets, classes are not perfectly linearly separable.
    • 










    

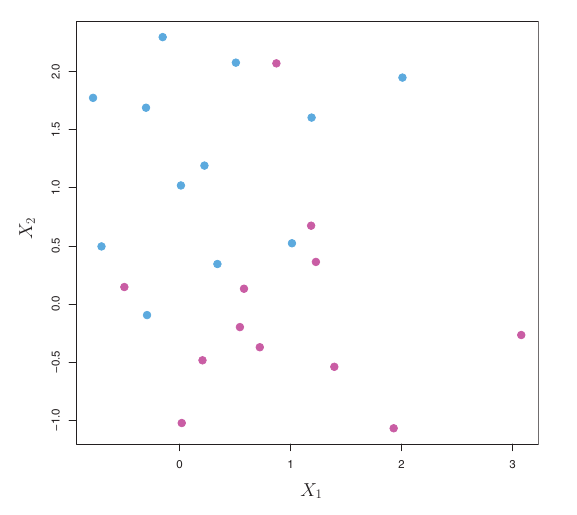
  • In such cases, there is no solution to the MMC optimization problem with \(M > 0\).
    • 





    

  • We need an extension that can handle overlapping classes. This leads to the Support Vector Classifier.
    • 









 
 
 
 
 





Support Vector Classifiers (SVC)









Support Vector Classifiers (SVC)





 


    

  • The Support Vector Classifier (SVC), or “soft margin classifier,” extends the MMC.
    • 






    

  • Motivation:

      

    1. Handles non-separable data.
      2. 

    2. More robust to individual observations: MMC can be very sensitive if adding one point dramatically changes the hyperplane. A tiny margin due to one outlier might not be ideal. 
      3. 

    • 







Support Vector Classifiers (SVC)










    

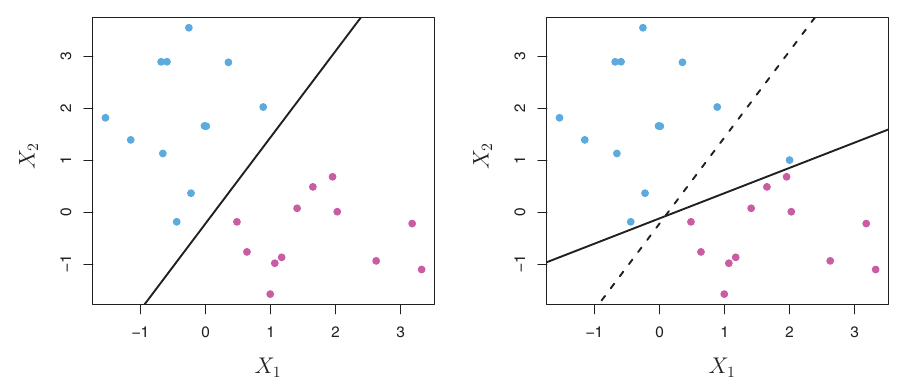
  • Idea: Allow some observations to be on the wrong side of the margin, or even on the wrong side of the hyperplane (misclassified).
    • 







SVC: Allowing Violations




    

  • The SVC aims for a hyperplane that separates most observations correctly, but tolerates some violations.
    • 

  • This involves a trade-off:

      

    • Wider margin (good for generalization).
      • 

    • Fewer margin violations (good fit to training data).
      • 

    • 

  • This is a bias-variance trade-off.
    • 














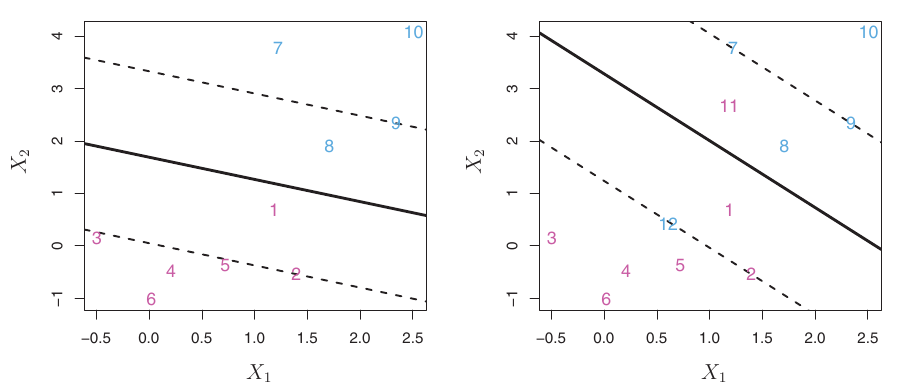
Details of the SVC







The SVC is the solution to the optimization problem:





Maximize \(M\) with respect to \(\beta_0, \dots, \beta_p, \epsilon_1, \dots, \epsilon_n, M\)





Subject to:


    

  1. \(\sum_{j=1}^p \beta_j^2 = 1\)
    2. 

  2. \(y_i (\beta_0 + \beta_1 x_{i1} + \dots + \beta_p x_{ip}) \ge M(1 - \epsilon_i) \quad \forall i\)
    3. 

  3. \(\epsilon_i \ge 0, \quad \sum_{i=1}^n \epsilon_i \le C\)
    4. 








Slack Variables \(\epsilon_i\) and Cost Parameter \(C\)




    

  • \(\epsilon_i\) are slack variables:

      

    • If \(\epsilon_i = 0\): \(x_i\) is on the correct side of the margin.
      • 

    • If \(\epsilon_i > 0\): \(x_i\) violates the margin (on the wrong side of the margin).
      • 

    • If \(\epsilon_i > 1\): \(x_i\) is on the wrong side of the hyperplane (misclassified).
      • 

    • 

  • \(C\) is a non-negative tuning parameter (cost parameter):

      

    • \(C\) is a budget for the total amount of slack (violations).
      • 

    • If \(C=0\): \(\epsilon_i\) must all be 0. This recovers the MMC (if data is separable).
      • 

    • If \(C > 0\): Allows some violations.

        

      • Small \(C\): Low budget for violations, margin will be narrow, classifier highly fits data (low bias, high variance). Many support vectors.
        • 

      • Large \(C\): High budget for violations, margin will be wider, classifier fits less hard (higher bias, lower variance). Fewer support vectors.
        • 

      • 

    • 

  • \(C\) is typically chosen via cross-validation.
    • 







SVC: Role of \(C\)











    

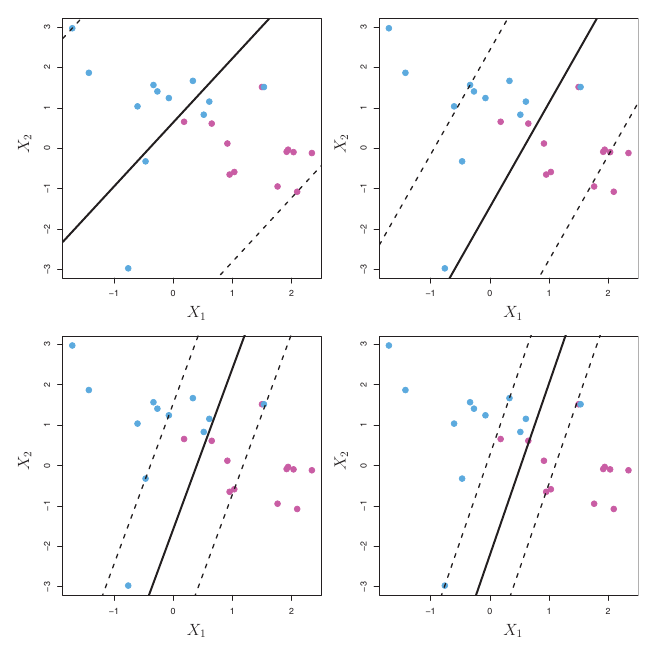
  • Small C: Narrow margin, few violations allowed. Fits training data closely. Potentially high variance.
    • 

  • Large C: Wider margin, more violations allowed. More robust to individual points. Potentially higher bias.
    • 

  • This is a key way to control the bias-variance trade-off for SVC.
    • 







Support Vectors in SVC





 


    

  • Observations that lie exactly on the margin or violate the margin (i.e., \(\epsilon_i > 0\) or \(y_i(\beta_0 + \sum \beta_j x_{ij}) = M\)) are the support vectors.
    • 





    

  • Observations strictly on the correct side of the margin (where \(\epsilon_i = 0\) and \(y_i(\beta_0 + \sum \beta_j x_{ij}) > M\)) do not affect the SVC solution.
    • 





    

  • The classifier’s decision boundary depends only on this subset of support vectors.
    • 





    

  • This makes SVCs robust to observations far from the boundary.
    • 









 
 
 
 
 





Support Vector Machines (SVM)









Support Vector Machines (SVM)



Classification with Non-linear Decision Boundaries





    

  • SVCs produce linear decision boundaries.
    • 

  • What if the true boundary is non-linear? 
    • 














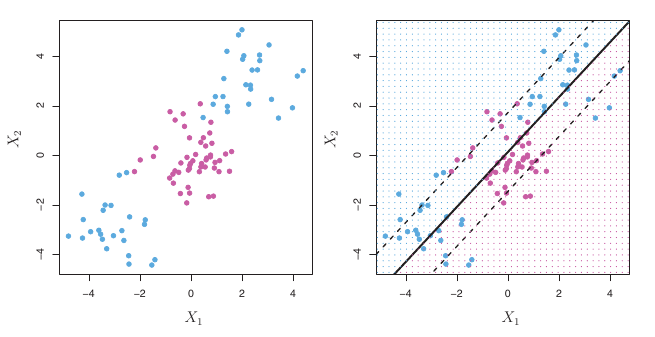
The SVM & Kernels







    

  • The Support Vector Machine (SVM) extends the SVC by using kernels to handle non-linear boundaries efficiently.
    • 

  • It turns out that the SVC solution (and classification rule) only involves inner products of observations: \(\langle x_i, x_{i'} \rangle = \sum_{j=1}^p x_{ij} x_{i'j}\).
    • 

  • The decision function can be written as: \[ f(x) = \beta_0 + \sum_{i \in \mathcal{S}} \alpha_i \langle x, x_i \rangle \] where \(\mathcal{S}\) is the set of indices of support vectors, and \(\alpha_i\) are parameters.
    • 

  • The key idea of SVMs: replace the inner product \(\langle x_i, x_{i'} \rangle\) with a more general kernel function \(K(x_i, x_{i'})\).
    • 







Kernels







    

  • A kernel \(K(x_i, x_{i'})\) is a function that quantifies the similarity between two observations \(x_i\) and \(x_{i'}\).
    • 

  • The decision function becomes: \[ f(x) = \beta_0 + \sum_{i \in \mathcal{S}} \alpha_i K(x, x_i) \]
    • 

  • Using a kernel \(K\) is often equivalent to implicitly mapping the data into a higher-dimensional feature space via some transformation \(\phi(x)\), and then computing the inner product in that space: \(K(x_i, x_{i'}) = \langle \phi(x_i), \phi(x_{i'}) \rangle\).
    • 

  • The “kernel trick”: we can compute \(K(x_i, x_{i'})\) directly without explicitly forming \(\phi(x_i)\), which might be very high-dimensional or even infinite-dimensional.
    • 







Common Kernels



Linear Kernel






 


    

  • Linear Kernel: \[K(x_i, x_{i'}) = \sum_{j=1}^p x_{ij} x_{i'j} = \langle x_i, x_{i'} \rangle\]
    • 






    

  • This recovers the Support Vector Classifier.
    • 

  • Measures similarity using Pearson correlation.
    • 







Common Kernels



Polynomial Kernel





    

  • Polynomial Kernel of degree \(d\): \[ K(x_i, x_{i'}) = (1 + \sum_{j=1}^p x_{ij} x_{i'j})^d = (1 + \langle x_i, x_{i'} \rangle)^d \] where \(d\) is a positive integer (tuning parameter).

      

    • Fits an SVM in a higher-dimensional space involving polynomials of degree \(d\).
      • 

    • If \(d=1\), it’s similar to the linear kernel (though the \(1+\) term makes it slightly different).
      • 

    • Can lead to much more flexible, non-linear decision boundaries.
      • 

    • 














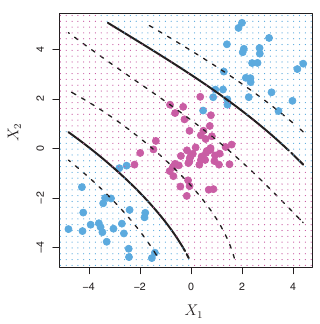
Common Kernels:



Radial Basis Function (RBF) Kernel





    

  • Radial Basis Function (RBF) Kernel (or Gaussian Kernel): \[ K(x_i, x_{i'}) = \exp \left( -\gamma \sum_{j=1}^p (x_{ij} - x_{i'j})^2 \right) = \exp(-\gamma \|x_i - x_{i'}\|^2_2) \] where \(\gamma > 0\) is a tuning parameter.

      

    • Similarity \(K(x_i, x_{i'})\) is high if \(x_i\) and \(x_{i'}\) are close in Euclidean distance, and low if they are far.
      • 

    • \(\gamma\) controls the “locality” or “reach” of the kernel.

        

      • Small \(\gamma\): broader similarity, smoother boundary.
        • 

      • Large \(\gamma\): more local similarity, potentially wigglier boundary.
        • 

      • 

    • The feature space for RBF kernels is implicitly infinite-dimensional!
      • 

    • 














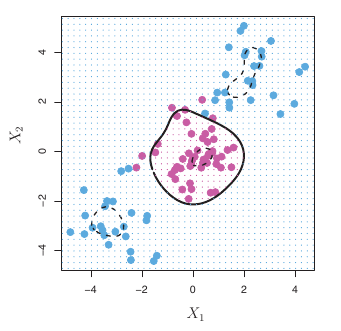
SVMs: Summary of Kernels







    

  • The choice of kernel and its parameters (e.g., \(d\) for polynomial, \(\gamma\) for RBF) are crucial and usually determined by cross-validation, along with the cost parameter \(C\).
    • 






    

  • Advantage of kernels: Computational efficiency. We only need to compute \(K(x_i, x_{i'})\) for all pairs of observations, not explicitly work in the (potentially huge) enlarged feature space.
    • 






    

  • The RBF kernel is very popular due to its flexibility.
    • 







SVMs with More than Two Classes




    

  • Standard SVMs are for binary classification. How to extend to \(K > 2\) classes?
    • 

  • Two main approaches:
    

      

    1. One-Versus-One (OVO) Classification:

        

      • Construct \(\binom{K}{2}\) SVMs, one for each pair of classes.
        • 

      • To classify a new observation, each of these \(\binom{K}{2}\) classifiers votes.
        • 

      • The observation is assigned to the class with the most votes.
        • 

      2. 

    2. One-Versus-All (OVA) Classification:

        

      • Fit \(K\) SVMs. The \(k\)-th SVM compares class \(k\) (coded as +1) against all other \(K-1\) classes (coded as -1).
        • 

      • To classify a new observation \(x^*\):

          

        • Compute the decision function value \(f_k(x^*)\) from each of the \(K\) SVMs.
          • 

        • Assign \(x^*\) to the class for which \(f_k(x^*)\) is largest (most confident prediction for that class).
          • 

        • 

      3. 

    • 










 
 
 
 
 





Support Vector Regression (SVR)









Support Vector Regression (SVR)







    

  • While SVMs are primarily for classification, an extension called Support Vector Regression (SVR) exists for quantitative responses.
    • 





    

  • SVR tries to find a function \(f(x)\) such that most training points \(x_i\) lie within an \(\epsilon\)-tube around \(f(x_i)\).
    • 





    

  • It also uses a loss function that only penalizes residuals larger in absolute value than some constant \(\epsilon\).

      

    • This is an \(\epsilon\)-insensitive loss function.
      • 

    • 





    

  • Kernels can be used with SVR to model non-linear relationships.
    • 





    

  • The “support vectors” in SVR are the points outside or on the boundary of this \(\epsilon\)-tube.
    • 







Predicting Value with SVR







    

  • To predict values, SVR first aims to find the optimal regression function \(f(x)\) that best fits the training data.
    • 





    

  • This involves solving an optimization problem that minimizes the \(\epsilon\)-insensitive loss while also keeping the model complexity (e.g., weights for linear SVR) low to prevent overfitting.
    • 





    

  • The goal is to find a function \(f(x)\) that generalizes well to unseen data.
    • 







The Prediction Process







    

  • Once the SVR model is trained and the optimal function \(f(x)\) (defined by its parameters and the support vectors) is determined:
    • 





    

  • Predicting a new value for an unseen input \(x_{new}\) is straightforward.
    • 





    

  • The “support vectors” are the critical data points that define the boundaries of the \(\epsilon\)-tube.
    • 





    

  • These are the only training points that directly contribute to the definition of the regression function \(f(x)\).
    • 





    

  • When predicting, the SVR model essentially uses the “essence” or learned parameters from these critical support vectors to determine the output for new inputs.

      

    • This is why SVR is sometimes called a “sparse” model; not all training points are needed for prediction.
      • 

    • 







Advantages of SVR for Prediction







    

  • SVR’s prediction capabilities benefit from several key features:
    • 





    

  • Robustness: Due to the \(\epsilon\)-insensitive loss function, it’s less sensitive to noise and outliers in the training data, leading to more stable predictions.
    • 





    

  • Non-linear Modeling: The use of kernels allows SVR to accurately predict complex, non-linear relationships that linear models cannot capture.
    • 





    

  • Generalization: By focusing on the margin of tolerance and penalizing model complexity (regularization), SVR aims to find a function that generalizes well to unseen data, providing reliable and accurate predictions.
    • 







Summary of Support Vector Machines




    

  • Maximal Margin Classifier: Simple, intuitive for linearly separable data. Maximizes margin.
    • 

  • Support Vector Classifier: Extends MMC to non-separable data using a “soft margin” (slack variables \(\epsilon_i\) and cost \(C\)). Produces linear boundaries.
    • 

  • Support Vector Machine: Extends SVC to non-linear boundaries using kernels (linear, polynomial, RBF). The “kernel trick” allows efficient computation in high-dimensional feature spaces.
    • 

  • Key ideas:

      

    • Maximizing the margin (classification) or fitting within an \(\epsilon\)-tube (regression).
      • 

    • Support vectors define the boundary/fit.
      • 

    • Tuning parameters (\(C\), kernel parameters like \(\gamma, d, \sigma\)) are crucial and chosen via CV.
      • 

    • 

  • SVMs are powerful for classification and regression.
    • 







Final Remarks







    

  • SVMs are a powerful and flexible class of supervised learning models.
    • 





    

  • Good performance in high-dimensional settings (\(p \gg n\)).
    • 





    

  • Robust due to reliance on support vectors.
    • 





    

  • Kernel choice and parameter tuning are critical for good performance.
    • 








References







Basics


    

  • Aprendizado de Máquina: uma abordagem estatística, Izibicki, R. and Santos, T. M., 2020, link: https://rafaelizbicki.com/AME.pdf.
    • 

  • An Introduction to Statistical Learning: with Applications in R, James, G., Witten, D., Hastie, T. and Tibshirani, R., Springer, 2013, link: https://www.statlearning.com/.
    • 

  • Mathematics for Machine Learning, Deisenroth, M. P., Faisal. A. F., Ong, C. S., Cambridge University Press, 2020, link: https://mml-book.com.
    • 








References







Complementaries