Statistical Machine Learning

Nonparametric Methods for Regression

Prof. Jodavid Ferreira

UFPE

Notation


  • \(X\) or \(Y\)
  • \(x\) or \(y\)
  • \(\mathbf{x}\) or \(\mathbf{y}\)
  • \(\dot{\mathbf{x}}\) or \(\dot{\mathbf{y}}\)
  • \(\mathbf{X}\) or \(\mathbf{Y}\)
  • \(\dot{\mathbf{X}}\) or \(\dot{\mathbf{Y}}\)


    

  • \(p\)
    • 

  • \(n\)
    • 

  • \(i\)
    • 

  • \(j\)
    • 

  • \(k\)
    • 





represent random variables (r.v.);


represent realizations of random variables;


represent random vectors;


represent realizations of random vectors;


represent random matrices;


represent realizations of random matrices;




dimension of features, variables


sample size


\(i\)-th observation, instance (e.g., \(i=1, ..., n\))


\(j\)-th feature, variable, parameter (e.g., \(j=1, ..., p\))


number of neighbors (KNN) or folds (CV)










 
 
 
 





k-Nearest Neighbors (KNN) Regression









k-Nearest Neighbors (KNN)



Regression








    

  • Core Idea:
    

      

    • To predict the response at a point \(\dot{\mathbf{x}}\), find the \(k\) training observations \((\dot{\mathbf{x}}_i, y_i)\) whose features \(\dot{\mathbf{x}}_i\) are closest to \(\mathbf{x}\). Average their responses \(y_i\).
      • 

    • 

  • One of the simplest nonparametric methods.
    • 





Given:


    

  • A target point \(\mathbf{x}\) (where we want to predict \(f(\mathbf{x})\)).
    • 

  • A distance metric \(d(\dot{\mathbf{x}}_i, \dot{\mathbf{x}}_j)\) (e.g., Euclidean distance).
    • 

  • The training data \(\{ (\dot{\mathbf{x}}_i, y_i) \}_{i=1}^n\).
    • 

  • The number of neighbors \(k\).
    • 









k-Nearest Neighbors (KNN)



Regression








    

  1. Find the set \(\mathcal{N}_{\mathbf{x}}\) containing the indices of the \(k\) points \(\dot{\mathbf{x}}_i\) in the training set that are closest to \(\mathbf{x}\) according to the distance metric. \[ \mathcal{N}_{\mathbf{x}} = \{ i \in \{1, \ldots, n\} \mid \dot{\mathbf{x}}_i \text{ is one of the } k \text{ closest points to } \mathbf{x} \} \]
    

    

    (Let \(d_{(k)}(\mathbf{x})\) be the distance to the k-th nearest neighbor of \(\mathbf{x}\). Then \(\mathcal{N}_{\mathbf{x}} = \{i \mid d(\dot{\mathbf{x}}_i, \mathbf{x}) \le d_{(k)}(\mathbf{x}) \}\), handling ties appropriately).*
    

    2. 





    

  1. The KNN regression estimate is the average of the responses for these neighbors: \[ \hat{f}_k(\mathbf{x}) = \frac{1}{k} \sum_{i \in \mathcal{N}_{\mathbf{x}}} y_i \]
    2. 









k-Nearest Neighbors (KNN)



Regression








    

  • Assumes that points close together in the predictor space \(\mathcal{X}\) likely have similar response values \(Y\).
    • 

  • Forms a local neighborhood and calculates a simple local average.
    • 

  • The “model” is just the training data itself. Prediction requires searching through the data.
    • 








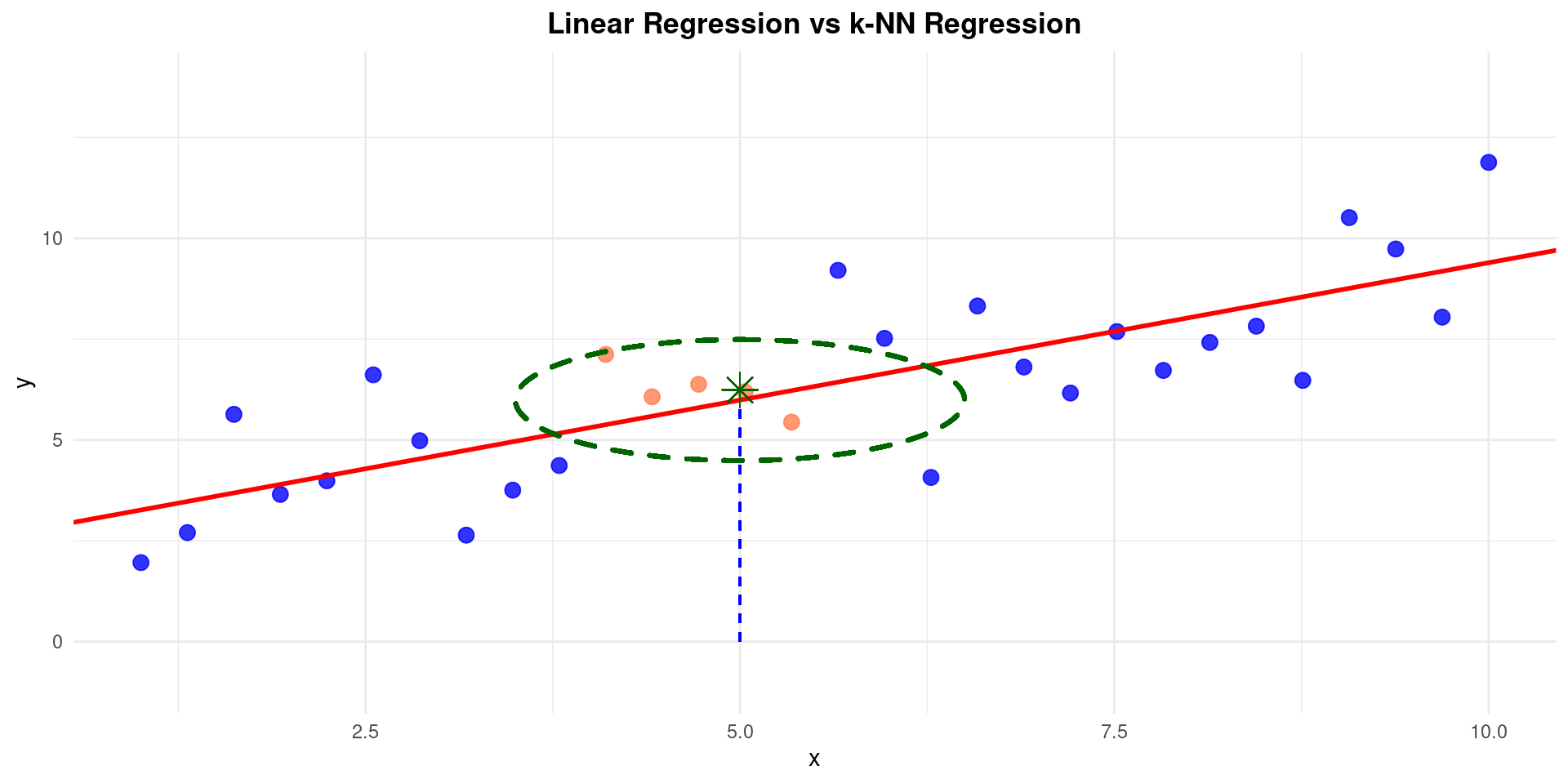
k-Nearest Neighbors (KNN)



Regression













k-Nearest Neighbors (KNN)



Tuning Parameter \(k\)





The \(k\) value is the number of neighbors, is the main tuning parameter.




    

  • Bias-Variance Trade-off for \(k\):

      

    • Small \(k\) (e.g., \(k=1\)):
      • 

    • Low bias (uses only the very closest points).
      • 

    • High variance (prediction is sensitive to noise in the single nearest neighbor).
      • 

    • Large \(k\) (e.g., \(k=n\)):
      

        

      • High bias (averages over many potentially dissimilar points; tends towards the global mean of \(Y\)).
        • 

      • Low variance (average of many points is stable). Very smooth fit (constant if \(k=n\)).
        • 

      • 

    • 







    

  • \(k\) is typically chosen using cross-validation.
    • 









k-Nearest Neighbors (KNN)



(Influence of \(k\))





Let’s revisit the 1D simulated data.



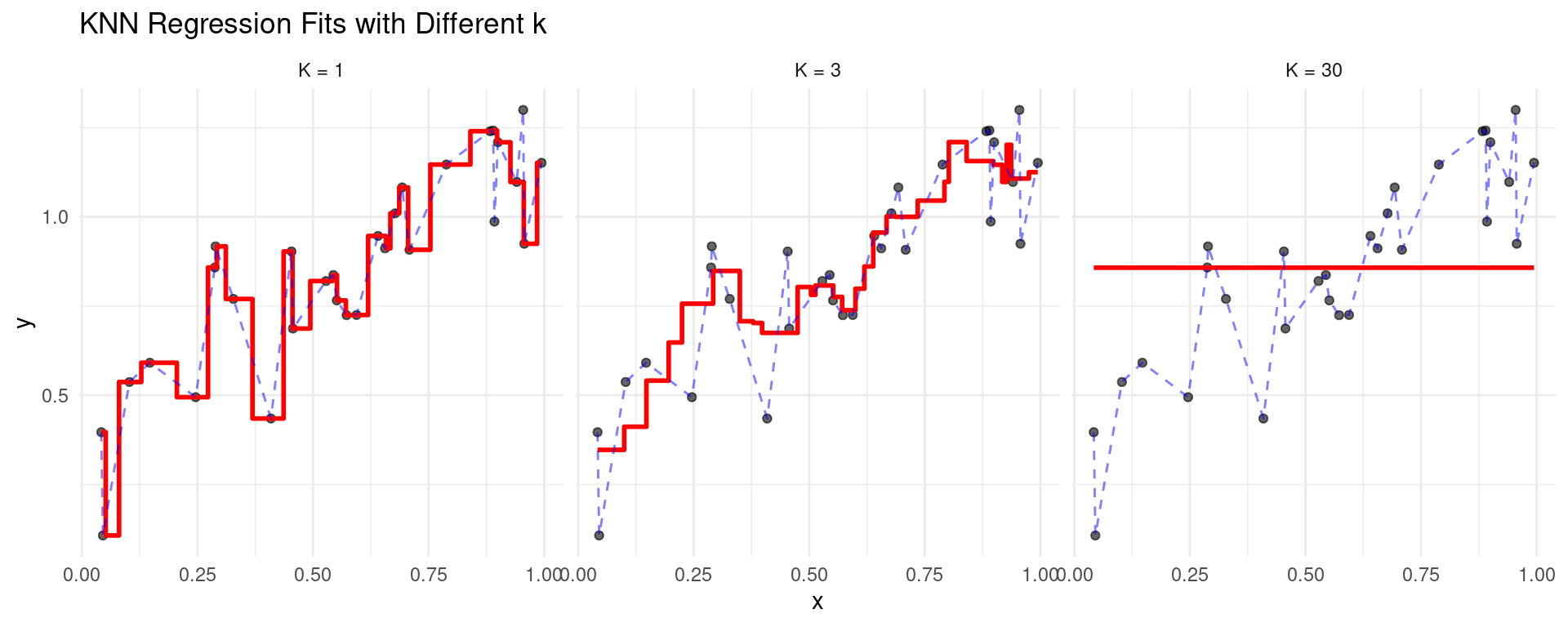
Note the characteristic “step function” appearance of KNN regression.






k-Nearest Neighbors (KNN)



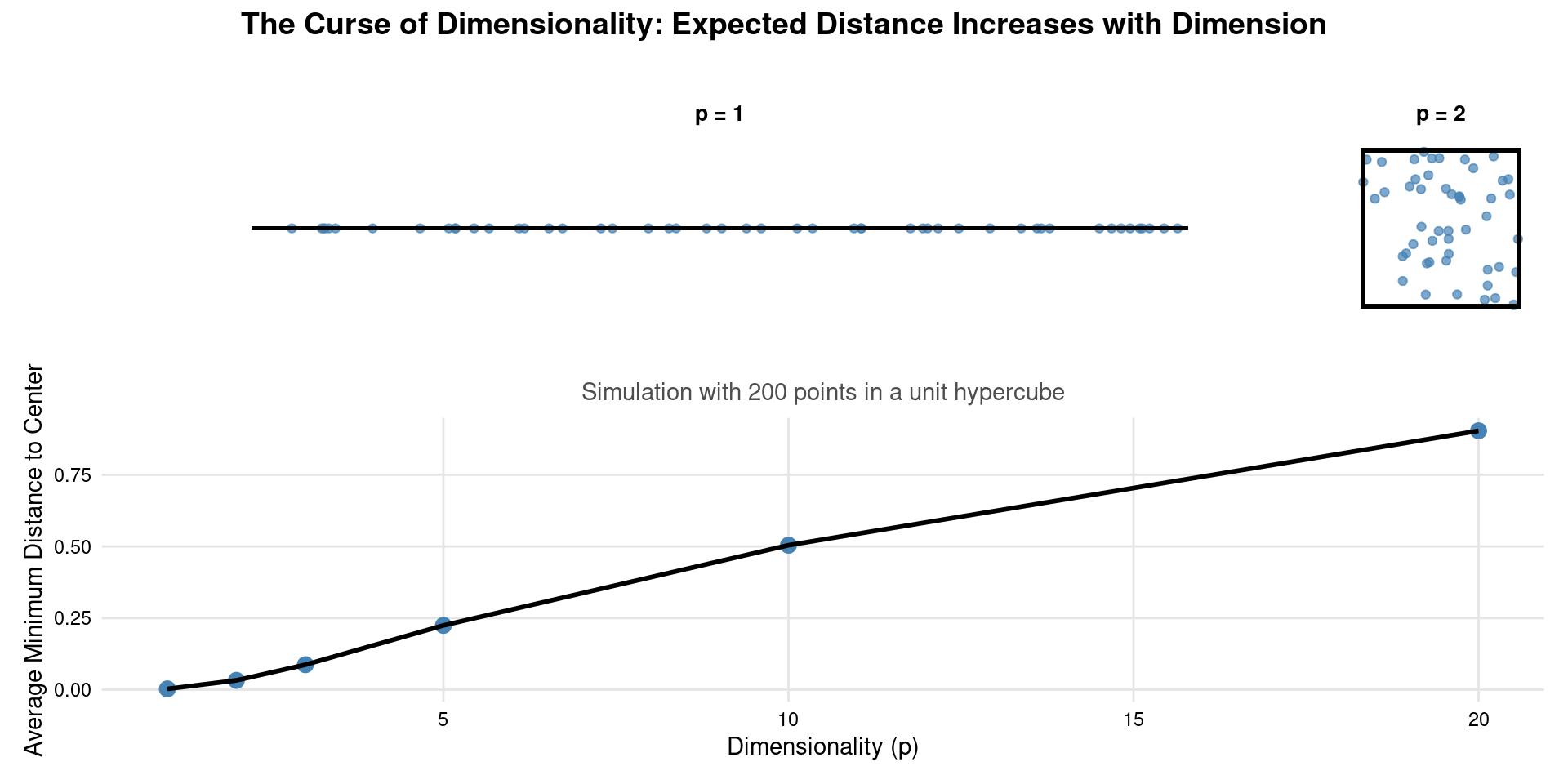
(Curse of Dimensionality)








    

  • KNN works reasonably well in low dimensions (\(p\) small).
    • 





    

  • In high dimensions (\(p\) large), the concept of “nearest neighbors” becomes less meaningful.

      

    • All points tend to be far away from each other.
      • 

    • The volume of the neighborhood needed to capture \(k\) points grows rapidly.
      • 

    • Points within the neighborhood may not be truly “local” in all dimensions.
      • 

    • Requires exponentially more data to maintain the density of points as \(p\) increases.
      • 

    • 





    

  • This is a major limitation of KNN in high-dimensional settings. Predictor scaling becomes very important.
    • 







k-Nearest Neighbors (KNN)



(Curse of Dimensionality)















 
 
 
 





Nadaraya-Watson Kernel Regression









Nadaraya-Watson Kernel Regression







    

  • A variation/improvement on KNN. Also based on local averaging, but uses a smooth weighting scheme instead of a hard cutoff.
    • 





    

  • Proposed independently by Nadaraya (1964) and Watson (1964).
    • 







    

  • Core Idea:
    

      

    • Assign weights \(w_i(\mathbf{x})\) to each training point \((\dot{\mathbf{x}}_i, y_i)\) based on how close \(\dot{\mathbf{x}}_i\) is to the target point \(\mathbf{x}\). Points closer to \(\mathbf{x}\) get higher weights. \[ \hat{f}(\mathbf{x}) = \sum_{i=1}^n w_i(\mathbf{x}) y_i \]
      • 

    • 









Nadaraya-Watson Kernel Regression



Weights








The weights are defined using a kernel function \(K\) and a bandwidth \(h\):


\[
w_i(\mathbf{x}) = \frac{K_h(d(\mathbf{x}, \dot{\mathbf{x}}_i))}{\sum_{j=1}^n K_h(d(\mathbf{x}, \dot{\mathbf{x}}_j))}
\]


where \(K_h(u) = K(u/h)\) is the scaled kernel function, \(K\) is the kernel profile (a non-negative function, usually symmetric around 0, integrating to 1), and \(d(\mathbf{x}, \dot{\mathbf{x}}_i)\) is the distance.


    

  • The weights sum to 1: \(\sum_{i=1}^n w_i(\mathbf{x}) = 1\).
    • 

  • The estimator is a weighted average of the responses \(y_i\).
    • 







Kernel Functions \(K(u)\)




The kernel function \(K(u)\) determines the shape of the weights. Common choices (for \(u \ge 0\), assuming distance \(d \ge 0\); often defined for \(u=d/h\)):


    

  • Uniform (Boxcar): \(K(u) = \frac{1}{2} \mathbb{I}(|u| \le 1)\)

      

    • Equivalent to KNN within distance \(h\). Assigns equal weight to neighbors within distance \(h\), zero weight outside. \[ K_h(d(\mathbf{x}, \dot{\mathbf{x}}_i)) \propto \mathbb{I}(d(\mathbf{x}, \dot{\mathbf{x}}_i) \le h) \]
      • 

    • 

  • Triangular: \(K(u) = (1 - |u|) \mathbb{I}(|u| \le 1)\)

      

    • Linearly decreasing weights. \[ K_h(d(\mathbf{x}, \dot{\mathbf{x}}_i)) \propto (1 - d(\mathbf{x}, \dot{\mathbf{x}}_i)/h) \mathbb{I}(d(\mathbf{x}, \dot{\mathbf{x}}_i) \le h) \]
      • 

    • 







Kernel Functions \(K(u)\)




    

  • Epanechnikov: \(K(u) = \frac{3}{4} (1 - u^2) \mathbb{I}(|u| \le 1)\)

      

    • Parabolic weights. Optimal in terms of minimizing asymptotic MSE. \[ K_h(d(\mathbf{x}, \dot{\mathbf{x}}_i)) \propto (1 - (d(\mathbf{x}, \dot{\mathbf{x}}_i)/h)^2) \mathbb{I}(d(\mathbf{x}, \dot{\mathbf{x}}_i) \le h) \]
      • 

    • 

  • Gaussian: \(K(u) = \frac{1}{\sqrt{2\pi}} e^{-u^2/2}\)

      

    • Smoothly decreasing weights, assigns non-zero (but potentially tiny) weight to all points. \[ K_h(d(\mathbf{x}, \dot{\mathbf{x}}_i)) \propto \exp\left(-\frac{d(\mathbf{x}, \dot{\mathbf{x}}_i)^2}{2h^2}\right) \]
      • 

    • 







Bandwidth \(h\): The Tuning Parameter




The bandwidth \(h > 0\) controls the width of the kernel, determining the size of the local neighborhood being averaged over.


    

  • Bias-Variance Trade-off for \(h\):

      

    • Small \(h\): Narrow kernel, uses only very close points.

        

      • Low bias.
        • 

      • High variance (wiggly fit).
        • 

      • 

    • Large \(h\): Wide kernel, averages over a large region.

        

      • High bias (oversmoothed fit).
        • 

      • Low variance.
        • 

      • 

    • 

  • \(h\) is the crucial tuning parameter, typically chosen via cross-validation.
    • 

  • The choice of kernel shape (\(K\)) usually has a smaller impact on performance than the choice of bandwidth \(h\).
    • 







Nadaraya-Watson Visualization



Influence of \(h\)





Using the Uniform kernel.




# Use ksmooth which implements Nadaraya-Watson
h_vals <- c(0.05, 0.2, 0.8) # Bandwidth h (span for ksmooth is different)
# ksmooth bandwidth 'h' corresponds to the full width 2h of the uniform kernel
# ksmooth 'bandwidth' argument seems different, maybe relates to h directly? Let's test.
x_grid <- seq(min(sim_data$x), max(sim_data$x), length.out = 100)
nw_preds_h <- list()

for (h_val in h_vals) {
  # Use kernel="box" for uniform
  fit <- ksmooth(x = sim_data$x, y = sim_data$y, kernel = "box", bandwidth = h_val, x.points = x_grid)
  nw_preds_h[[as.character(h_val)]] <- data.frame(x = fit$x, pred = fit$y, h = h_val)
}
nw_pred_h_df <- bind_rows(nw_preds_h)








Nadaraya-Watson Visualization



Influence of \(h\)





Using the Uniform kernel.







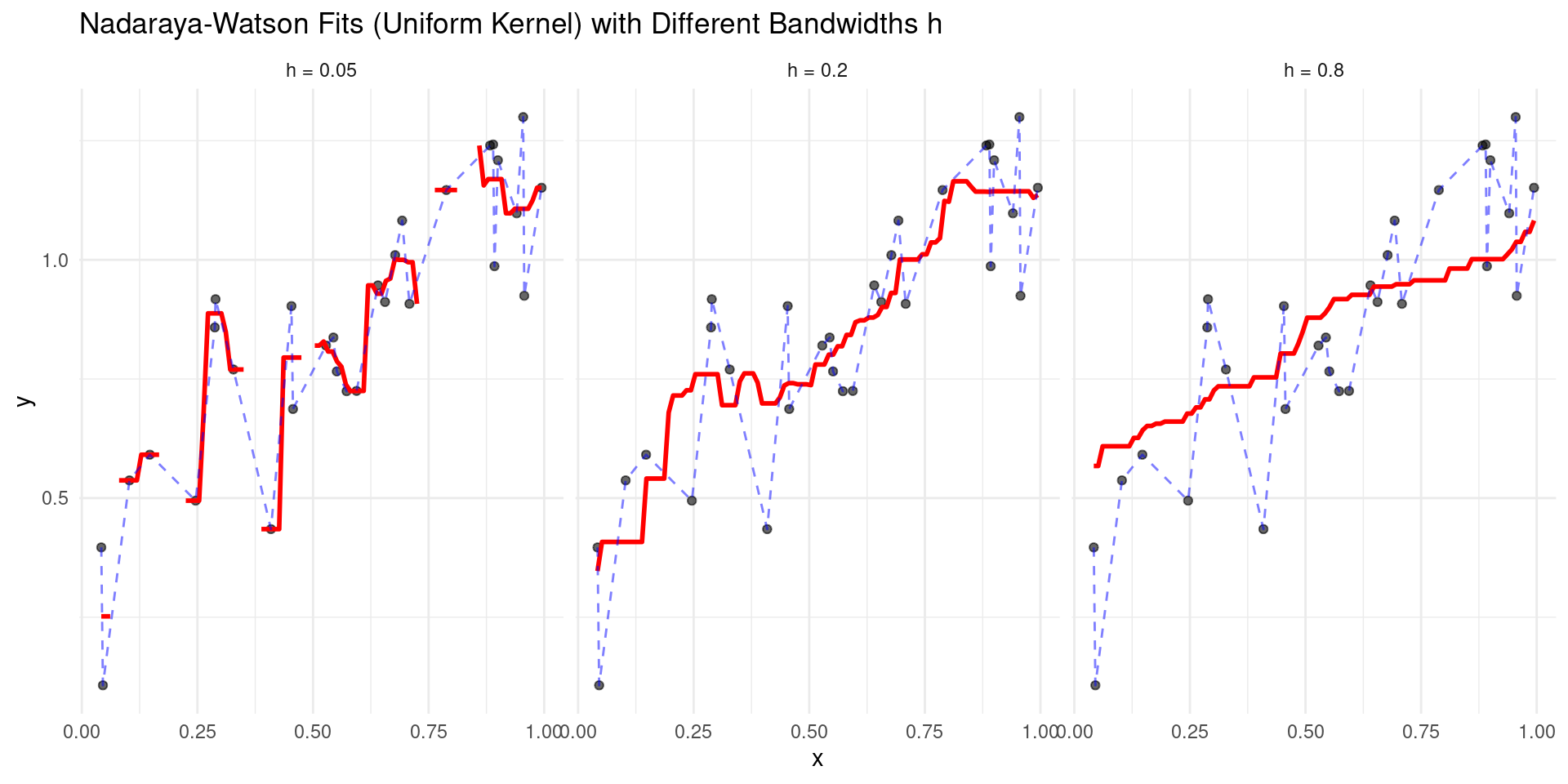
Nadaraya-Watson Visualization



Influence of Kernel





Comparing Uniform (“box”) and Gaussian (“normal”) kernels with the same bandwidth \(h=0.1\).







h_fixed <- 0.1
kernels <- c("box", "normal")
nw_preds_k <- list()

for (k_name in kernels) {
  fit <- ksmooth(x = sim_data$x, y = sim_data$y, kernel = k_name, bandwidth = h_fixed, x.points = x_grid)
  nw_preds_k[[k_name]] <- data.frame(x = fit$x, pred = fit$y, kernel = k_name)
}
nw_pred_k_df <- bind_rows(nw_preds_k)







    

  • Gaussian kernel gives a smoother result than the uniform kernel.
    • 







Nadaraya-Watson Visualization



Influence of Kernel





Comparing Uniform (“box”) and Gaussian (“normal”) kernels with the same bandwidth \(h=0.1\).






    

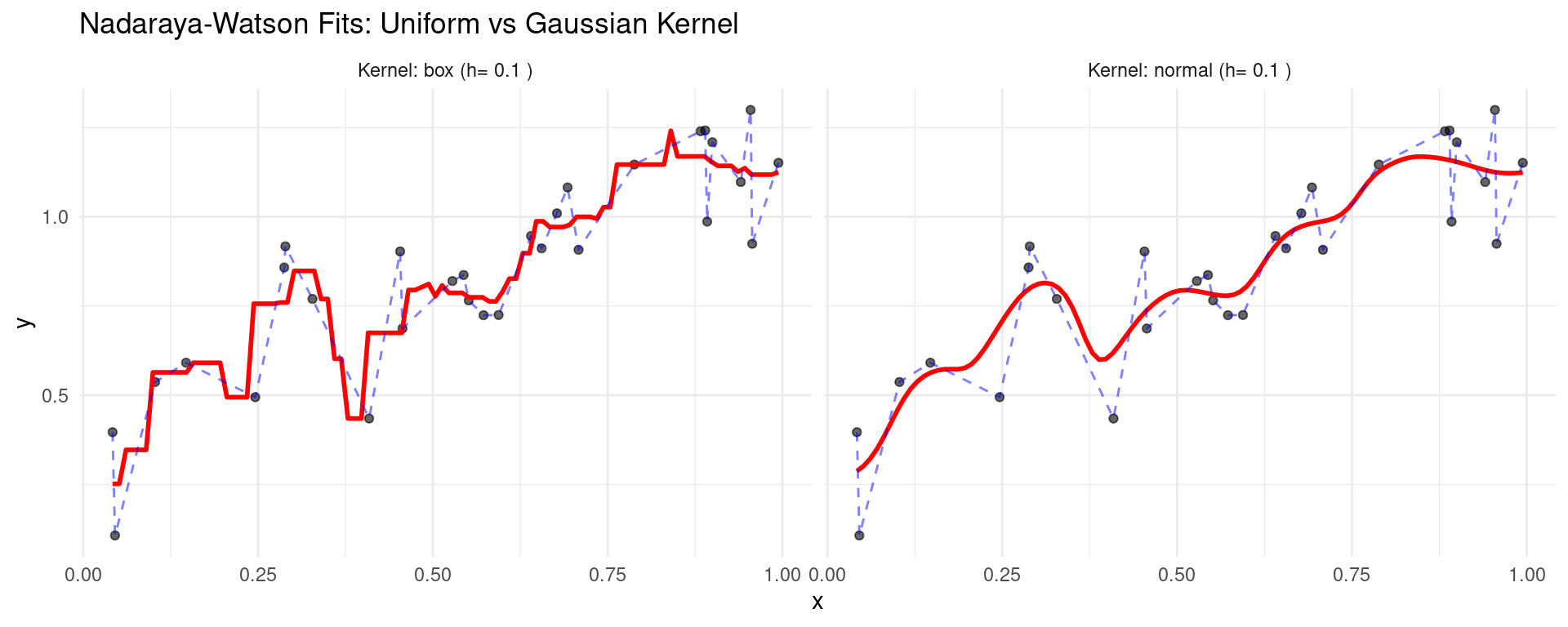
  • Gaussian kernel gives a smoother result than the uniform kernel.
    • 








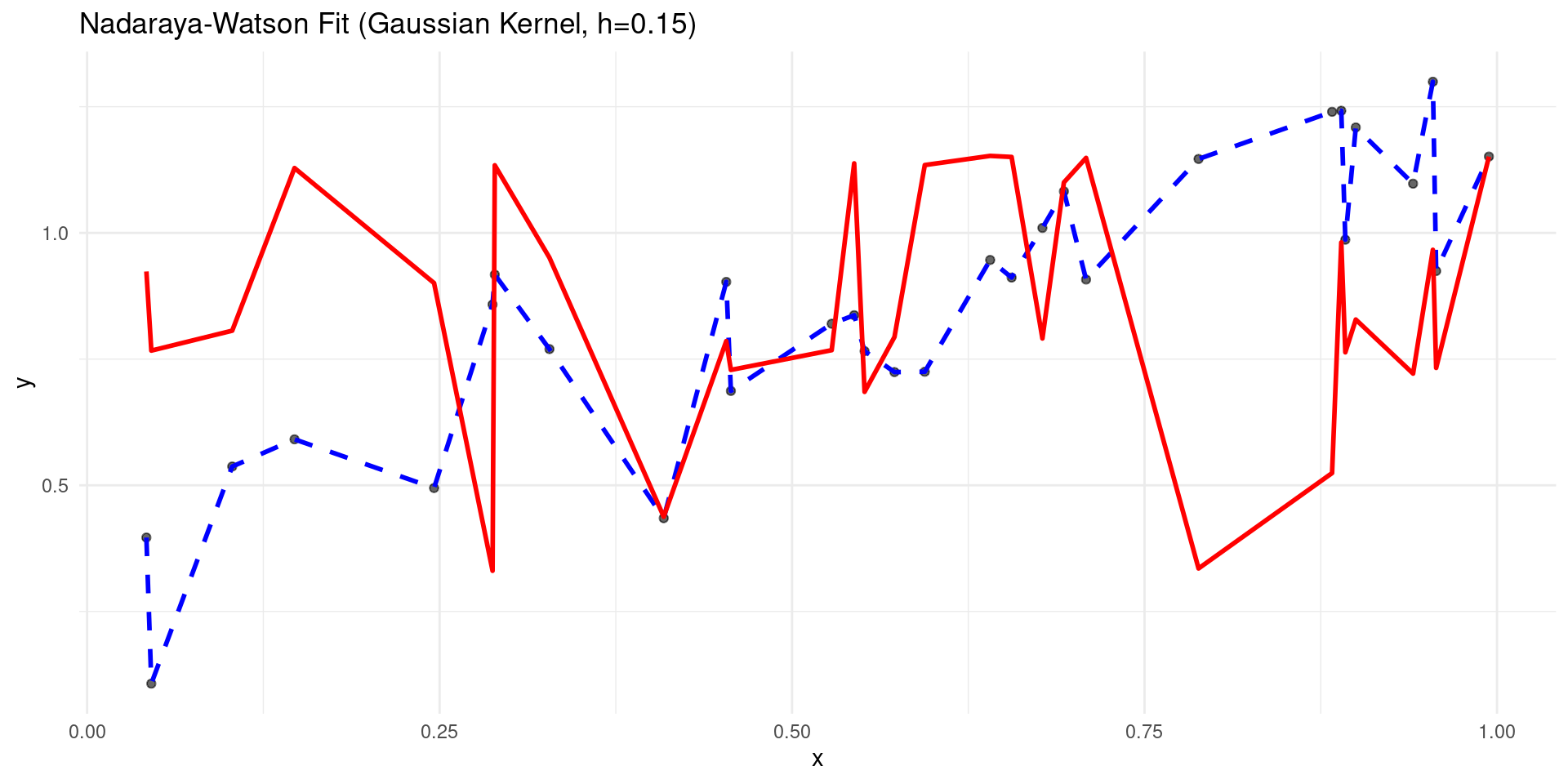
R Example: Nadaraya-Watson



ksmooth








R’s stats::ksmooth function performs Nadaraya-Watson regression.




# Using ksmooth
h_choice <- 0.15 # Chosen via CV, perhaps
fit_ks <- ksmooth(x = sim_data$x, y = sim_data$y,
                  kernel = "normal", # Gaussian kernel
                  bandwidth = h_choice,
                  x.points = sim_data$x) # Predict at original points

sim_data$pred_ksmooth <- fit_ks$y

p <- ggplot(sim_data, aes(x = x)) +
  geom_point(aes(y = y), alpha = 0.6) +
  geom_line(aes(y = y_true), color = "blue", linewidth = 1, linetype = "dashed") +
  geom_line(aes(y = pred_ksmooth), color = "red", linewidth = 1) +
  labs(title = paste("Nadaraya-Watson Fit (Gaussian Kernel, h=", h_choice, ")", sep="")) +
  theme_minimal()








R Example: Nadaraya-Watson



ksmooth








R’s stats::ksmooth function performs Nadaraya-Watson regression.








Summary: Methods Covered




    

  • k-Nearest Neighbors (KNN): Predict using the average response of the \(k\) closest training points. Simple, intuitive, but can be slow and sensitive to \(p\).
    • 

  • Nadaraya-Watson: Predict using a weighted average, with weights determined by a kernel function \(K\) and bandwidth \(h\).
    • 

  • All these methods involve tuning parameters (\(k\) or \(h\)) that control the bias-variance trade-off.
    • 

  • Cross-validation is essential for choosing these parameters.
    • 

  • Understanding the underlying assumptions and trade-offs is key to applying these methods effectively.
    • 








References







Basics


    

  • Aprendizado de Máquina: uma abordagem estatística, Izibicki, R. and Santos, T. M., 2020, link: https://rafaelizbicki.com/AME.pdf.
    • 

  • An Introduction to Statistical Learning: with Applications in R, James, G., Witten, D., Hastie, T. and Tibshirani, R., Springer, 2013, link: https://www.statlearning.com/.
    • 

  • Mathematics for Machine Learning, Deisenroth, M. P., Faisal. A. F., Ong, C. S., Cambridge University Press, 2020, link: https://mml-book.com.
    • 








References







Complementaries